What Are Triangles?

A triangle is a shape that is comprised by enclosing three straight lines in the same plane. In mathematics, triangles are an integral part of geometry. Since any closed figure having more than two sides can be said to be a polygon, triangles are polygons as well.  

General Properties of Triangles

In a triangle, there are three sides and three angles. The sum of the interior angles will always be 180 degrees. This is the triangle’s angle sum property. Similarly, the sum of the exterior angles of a triangle is always 360 degrees. A triangle is denoted by the symbol ∆. ∆ ABC denotes a triangle whose three vertices are A, B, and C, and the sides are AB, BC, and CA. 

What are the Different Triangles?

There are six types of different triangles. However, these six types can be further subdivided into two groups. 

The types of triangles are based on the measurements of the triangles' angles and the lengths of their sides. The different properties of these types of triangles are also based on these differences in sides and angles. 

What are the Different Types of Triangles Based on their Sides?

Based on their side length, a triangle can be categorized as:

• Scalene 
• Isosceles 
• Equilateral 

We discuss these types in detail below. 

Scalene Triangle 

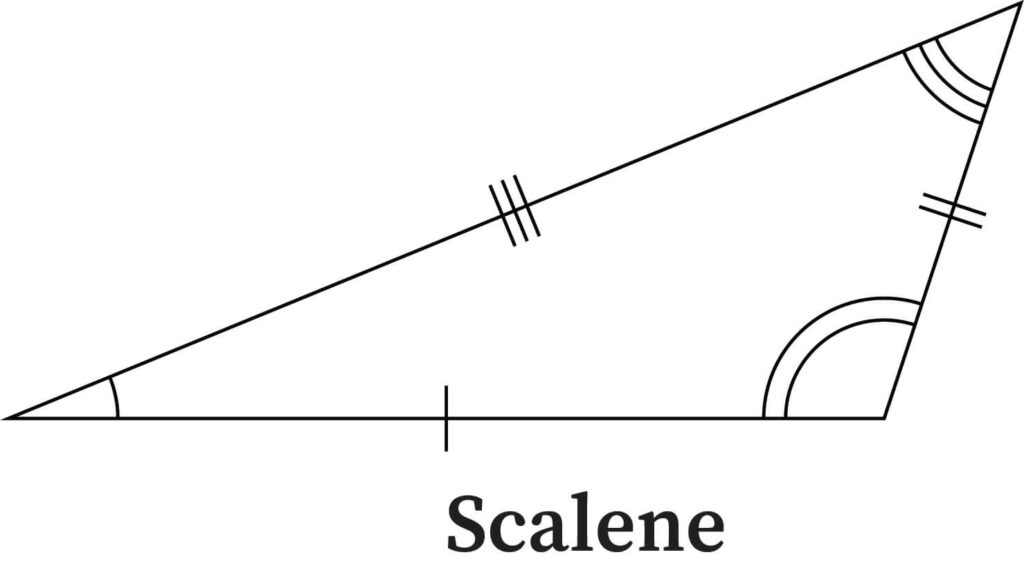
A scalene is a triangle that has different lengths in all of its three sides. There is no way to determine what the length of sides in a scalene triangle will be. All three sides will be different. Since scalene triangles have different side lengths, their interior angles are also all of different measurements. This means that none of the angles in a scalene triangle are equal. This type of triangle is truly random in nature. 

Isosceles Triangle 

An isosceles triangle is a special type of triangle. In this type, the length of the sides is different as well. However, contrary to the scalene, an isosceles triangle has two sides of the same length. Only the third side will be of a different length than the other two.

Any two sides of this triangle can have the same length. This means that interior angles formed opposite of those equal sides are also equal in measurement. In an isosceles triangle, there are a total of two equal angles and two equal sides. 

Equilateral Triangle 

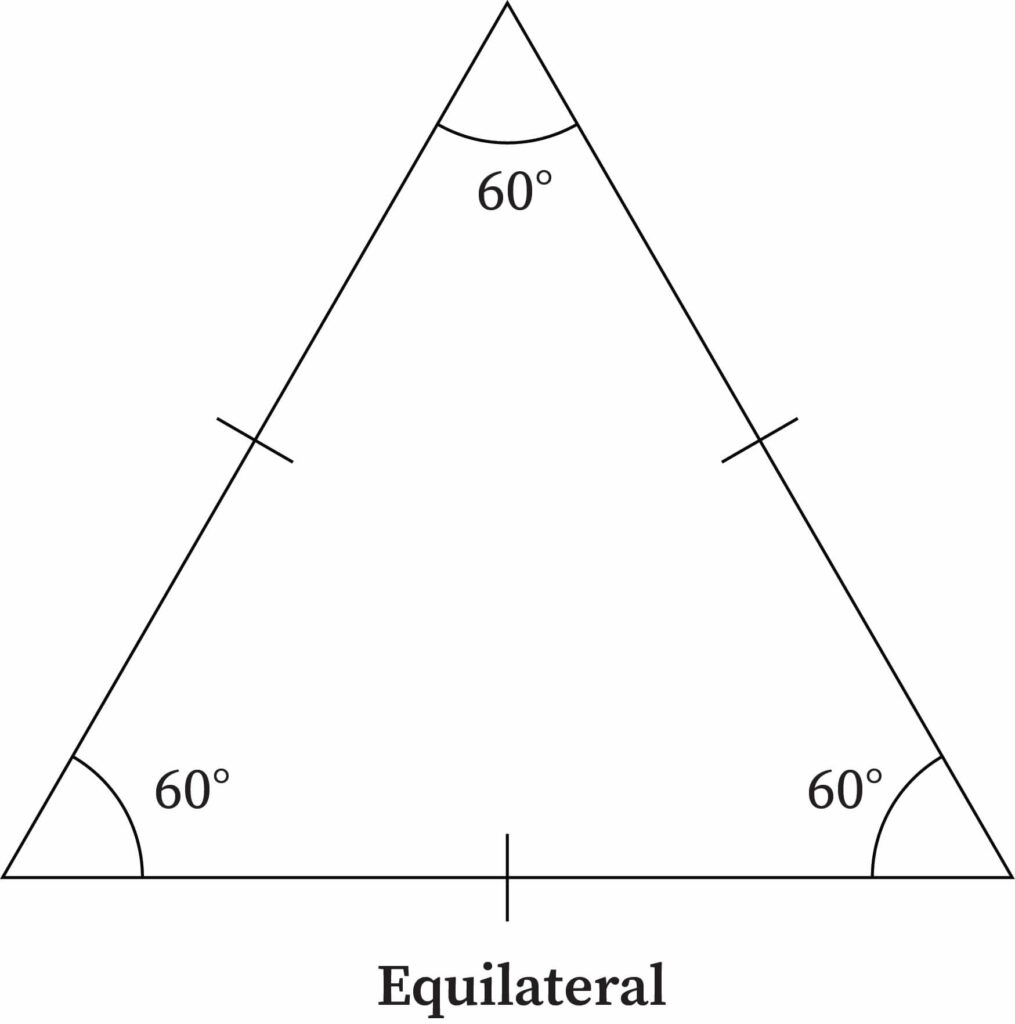
An equilateral triangle is perhaps the most perfect type of triangle. Unlike isosceles triangles or scalene triangles, all three sides are exactly equal in length in an equilateral triangle. This means that if you know the length of any one side, you will know the length of all three sides.

Since the three sides are of equal length, the interior angles formed are also equal in nature. As the total sum of angles is always 180 degrees for a triangle, each angle in an equilateral triangle is 180/3, or 60 degrees. Another name for an equilateral triangle is equiangular triangle. Calculation on this type of triangle is considered to be the easiest. 

What are the Types Based on their Angles? 

Next, we have the types of triangles based on the measurement of their angles. The types are as follows: 

• Acute-angled 
• Obtuse-angled 
• Right-angled 

These types of triangles are discussed below. 

Acute-Angled Triangle 

In an acute-angled triangle, all of the three interior angles are acute. An acute angle is an angle between 0 degrees and 90 degrees. If all the angles of a triangle are acute, then the triangle is said to be an acute-angled triangle. Since the angles of an equilateral triangles are all 60 degrees, this is an example of an acute-angled triangle. 

Obtuse-Angled Triangle 

As the name suggests, an obtuse-angled triangle is a triangle in which any one of the three interior angles is obtuse in nature. An obtuse angle is an angle that measures between 90 degrees and 180 degrees. As the total sum of angles is always 180 degrees in a triangle, all three angles can never be obtuse. In an obtuse-angled triangle, one angle is obtuse, and the other two are always acute in nature. 

Right-Angled Triangle 

In a right-angled triangle, one of the angles is a right angle. In other words, one angle is exactly 90 degrees. This means that the other two angles are both acute in nature, as per the angle sum property of triangles.

In this type, the two sides that form the right angle are always perpendicular to each other. The third side, which is the opposite side of the right angle, is known as the hypotenuse. This side also has the greatest length of the three sides in a right-angled triangle. This can also be called right-angled isosceles if the two perpendicular sides are of the same length. 

What are Similar Triangles?

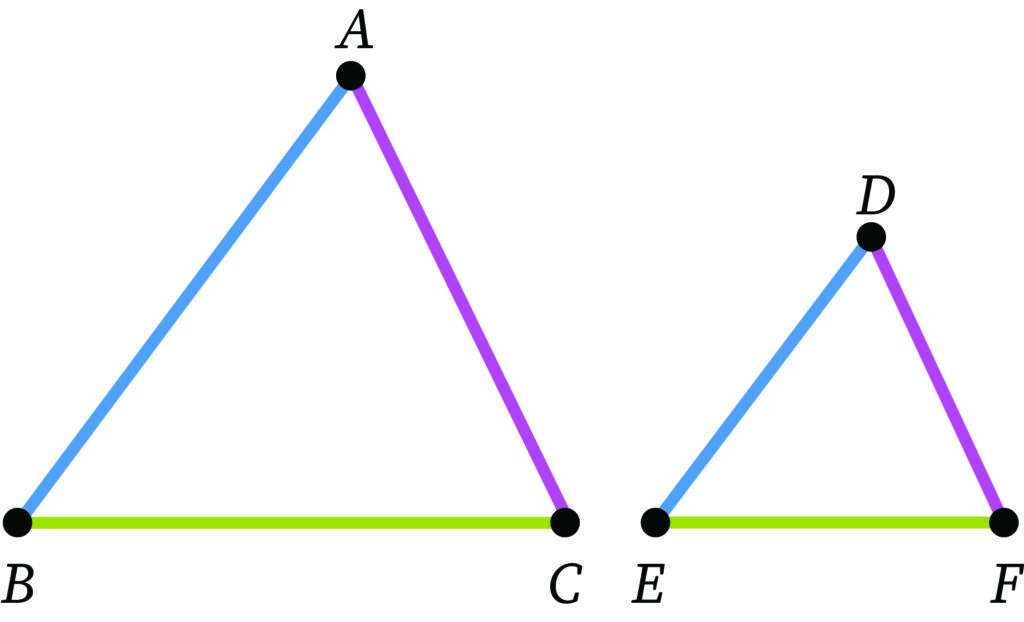
Two triangles are said to be similar when both triangles follow some criteria. There are four ways to determine the similarity of two triangles. They are as follows: 

SSS or Side-Side-Side Similarity 

Two triangles will be similar if their corresponding side lengths have the same ratio. In such a case, the corresponding angles of the two triangles will also be of equal value. 

AAA or Angle-Angle-Angle Similarity

Two triangles are similar if their corresponding angles are of the same value. This is a corollary to SSS (side-side-side) similarity. In such cases, the corresponding sides of the two triangles will have an equal ratio as well. 

SAS or Side-Angle-Side Similarity

Two triangles are similar if they have an angle of the same value, and the sides forming this angle in the two triangles also have the same ratio. 

AA or Angle-Angle Similarity 

If two triangles share a pair of angles of the same value, then they are similar. In such cases, the value of any two angles of the first triangle will be the same as the value of any two angles of the second triangle. 

Practice Problem

If ∆ ABC is right-angled at B, and it is also an isosceles triangle, find the value of A and C. 

As ABC is a right-angled isosceles at B, AB and AC will have the same length. 

As B = 90 degrees, the sum of angles of A and C will be 180 – 90 degrees, or 90 degrees. 

Also, here B = C, as ABC is an isosceles triangle. 

Therefore, we have B + C = 90 degrees. 

Or, 2B = 2C = 90 degrees B = C = 90/2 = 45 degrees, which is the required answer. 

Formulas

Context and Applications

In real life, triangles are important figures that are required in complex construction procedures. Also, the properties of triangles come in handy when the measurement of the inclined angles needs to be figured out. 

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for:

• B.S. in Mathematics 
• M.S. in Mathematics