What are Trigonometric Identities?

Trigonometry in mathematics deals with the right-angled triangle’s angles and sides. By trigonometric identities, we mean the identities we use whenever we need to express the various trigonometric functions in terms of an equation.

Why do we Use Trigonometric Identities?

The trigonometric identities help us to denote and relate the various sides and angles of a right-angled triangle. The concept of trigonometric identities came from the Pythagoras theorem. It states that the square of the hypotenuse, which is the longest side of a right-angled triangle, is equal to the sum of the squares of the other two sides. Every trigonometric identity has been devised with the help of the hypotenuse and the other two sides. Creating equations that can be expressed in terms of these sides and the angle formed between them, we can come up with the identities in trigonometry.

These identities are true for both equalities and inequalities. There are multiple angles and functions involved in these identities. When we need to describe the side or angle of a triangle, we use the various relations that exist between the trigonometric functions. However, only right-angled triangles can be expressed as per their sides and angles with trigonometric identities.

What do we mean by Identity?

Every equation cannot be an identity. Only when an equation holds for every possible case, then we can call it an identity. In the case of a trigonometric equation, only when the equation holds for all of the angular values involved in it, then we call it a trigonometric identity. Identities can be established by many methods. The most common one is by reducing any one or both sides of the equations so that a required modified form can be attained.

It is important to understand the trigonometric or trig identities for solving trigonometric expressions or equations. However, to understand the identities properly, we must know about the ratios that exist in trig as well.

What do we mean by Trigonometric Ratios?

We now discuss trigonometric ratios. There are six fundamental ratios that we use in trigonometry. They are-

• Sine (sin)
• Cosine (cos)
• Tangent (tan)
• Cosecant (cosec)
• Secant (sec)
• Cotangent (cot)

If we consider a right-angled triangle, all of the six basic trigonometric ratios can be described. We generally use the ratios of the triangle’s sides, like the hypotenuse, opposite, and adjacent sides to express these trigonometric ratios. Every single trigonometric identity has been formed from the trigonometric ratios. Hence, it is very important to understand the ratios of trig as well.

How do we express Trigonometric Ratios?

Usually, the trigonometric ratios are expressed with the help of angles. In general cases, the angle ‘θ’ or theta is used. We use the basic six trigonometric ratios with the help of θ as follows-

• Sin θ is the ratio of the opposite side of θ to the hypotenuse.
• Cos θ is the ratio of the adjacent side of θ to the hypotenuse.
• Tan θ is the ratio of the opposite side of θ to the adjacent side of θ. It can also be said to be the ratio of sin θ and cos θ.
• Cot θ is the ratio of the adjacent side of θ to the opposite side of θ. It can also be said to be the ratio of 1 and tan θ.
• Sec θ is the ratio of the hypotenuse to the adjacent side of θ. It is also expressed as the ratio of 1 and cos θ.
• Cosec θ is the ratio of the hypotenuse to the opposite side of θ. It is alternatively expressed as the ratio of 1 and sin θ.

In a right-angled triangle, the adjacent side of θ is the base of the triangle, and the opposite side is the perpendicular. The side joining these two sides is known as the hypotenuse, and it is also the longest side in the triangle.

Formula

Now, we describe the various trigonometric identities and their formula. It is important to know about these identities as these can help in solving various trigonometric problems.

All of the basic identities of trigonometry have been given below.

What are Reciprocal Identities?

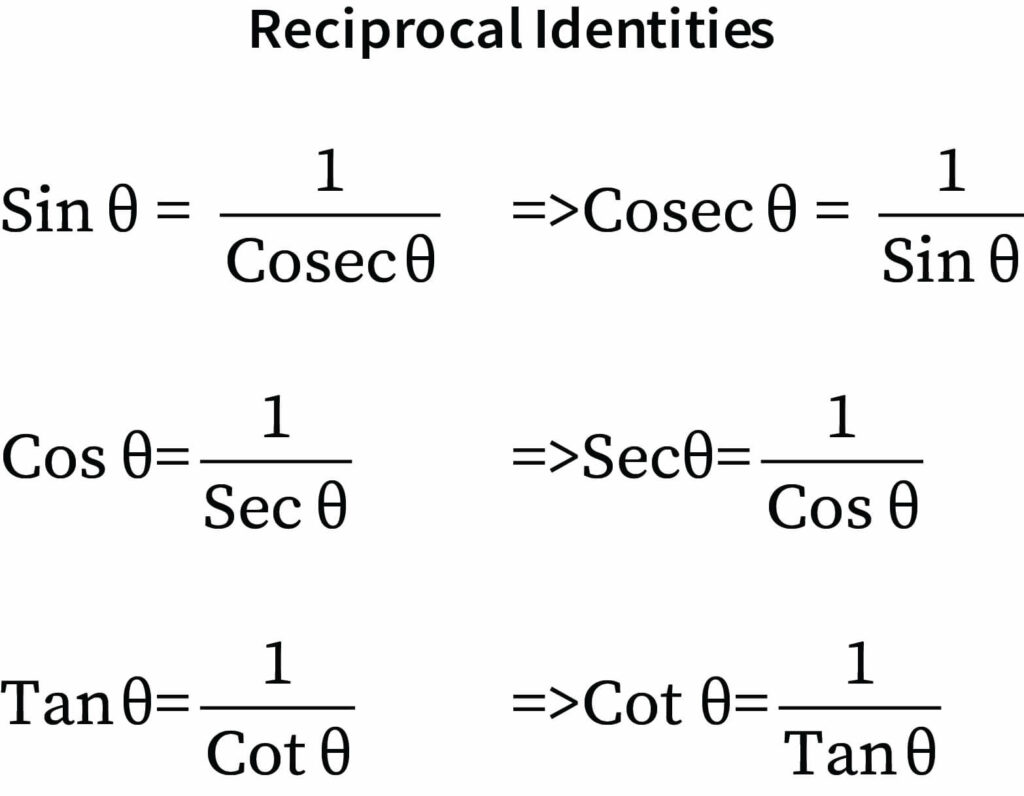
By reciprocal identities, we mean the trigonometric functions that are related to each other by reciprocating one another. They are as follows-

$$\begin{array}{l}\text{Sin θ = }\frac{\text{1}}{\text{Cosec θ}}\\ \text{=>Cosec θ = }\frac{\text{1}}{\text{Sin θ}}\\ \\ \text{Cos θ=}\frac{\text{1}}{\text{Sec θ}}\\ \text{=>Secθ=}\frac{\text{1}}{\text{Cos θ}}\\ \\ \text{Tan θ=}\frac{\text{1}}{\text{Cot θ}}\\ \text{=>Cot θ=}\frac{\text{1}}{\text{Tan θ}}\end{array}$$

Here, we can see that sine and cosecant, cosine and secant, and tangent and cotangent are reciprocals of each other.

What are Pythagorean Identities?

By Pythagorean identities, we mean the trigonometric functions that are related to each other by the Pythagoras theorem. They are as follows-

What are the Ratio Identities?

By ratio identities, we mean the trigonometric functions that are related to each other in the form of a ratio. They are as follows-

We only have tan and cot as the proper ratio identities.

What are Opposite Angle Identities?

By opposite angle identities, we mean the trigonometric functions that are related to each other in the form of their opposite angles. Here cosine and secant are even functions. Sine, tangent, cotangent, and cosecant are odd functions. They are as follows-

What are Complementary Angles Identities?

By complementary angles identities, we mean the trigonometric identities that can be expressed in the form of their complementary angles. They are as follows-

What are Angle Sum and Difference Identities?

The trigonometric identities that can be expressed by the sum and difference of two angles are known as angle sum identities and angle difference identities.

If we consider the two angles as ‘A’ and ‘B’, then the identities are –

$$\begin{array}{l}\text{sin }\left(\text{A+B}\right)\text{ = sin A}\text{.cos B + cos A}\text{.sin B}\\ \text{sin }\left(\text{A-B}\right)\text{ = sin A}\text{.cos B - cos A}\text{.sin B}\\ \text{cos }\left(\text{A+B}\right)\text{ = cos A}\text{.cos B - sin A}\text{.sin B}\\ \text{cos }\left(\text{A-B}\right)\text{ = cos A}\text{.cos B + sin A}\text{.sin B}\\ \text{tan }\left(\text{A+B}\right)\text{ = }\frac{\text{tan A + tan B}}{\text{1 - tan A}\text{.tan B}}\\ \text{tan }\left(\text{A-B}\right)\text{ = }\frac{\text{tan A - tan B}}{\text{1 + tan A}\text{.tan B}}\end{array}$$

However, there are trigonometric identities for three angles as well. If we consider any three angles as A, B, and C respectively, then we have the following identities-

$$\begin{array}{l}\text{sin }\left(\text{A+B+C}\right)\text{ = sin A}\text{.cos B}\text{.cos C + cos A}\text{.sin B}\text{.cos C + cos A}\text{.cos B}\text{.sin C - sin A}\text{.sin B}\text{.sin C}\\ \\ \text{cos }\left(\text{A+B+C}\right)\text{ = cos A}\text{.cos B}\text{.cos C - cos A}\text{.sin B}\text{.sin C - sin A}\text{.cos B}\text{.sin C - sin A}\text{.sin B}\text{.cos C}\\ \\ \text{tan }\left(\text{A+B+C}\right)\text{ = }\frac{\text{tan A + tan B + tan C - tan A}\text{.tan B}\text{.tan C}}{1\text{ - tan A}\text{.tan B - tan B}\text{.tan C - tan A}\text{.tan C}}\\ \\ \text{cot }\left(\text{A+B+C}\right)\text{ = }\frac{\text{cot A}\text{.cot B}\text{.cot C - cot A - cot B - cot C}}{\text{cot A}\text{.cot B + cot B}\text{.cot C + cot A}\text{.cot C}}\end{array}$$

If angles A, B, and C are the three angles of the same triangle, then the following identities hold:

$$\begin{array}{l}\text{sin A}\text{.cos B}\text{.cos C + cos A}\text{.sin B}\text{.cos C + cos A}\text{.cos B}\text{.sin C = sin A}\text{.sin B}\text{.sin C}\\ \text{cos A}\text{.sin B}\text{.sin C + sin A}\text{.cos B}\text{.sin C + sin A}\text{.sin B}\text{.cos C = 1 + cos A}\text{.cos B}\text{.cos C}\\ \text{tan A + tan B + tan C = tan A}\text{.tan B}\text{.tan C}\\ \text{cot B}\text{. cot C + cot C}\text{.cot A + cot A}\text{.cot B = 1}\\ \text{tan }\frac{\text{B}}{\text{2}}.\text{tan }\frac{\text{C}}{\text{2}}\text{ + tan }\frac{\text{C}}{\text{2}}.\tan \frac{\text{A}}{\text{2}}\text{ + tan }\frac{\text{A}}{\text{2}}\text{.tan }\frac{\text{B}}{\text{2}}\text{ = 1}\\ \text{cot }\frac{\text{A}}{\text{2}}\text{ + cot }\frac{\text{B}}{\text{2}}\text{ + cot }\frac{\text{C}}{\text{2}}\text{ = cot }\frac{\text{A}}{\text{2}}.\text{cot }\frac{\text{B}}{\text{2}}.cot\frac{\text{C}}{\text{2}}\\ \text{sin 2A + sin 2B + sin 2C = 4 sin A}\text{.sin B}\text{.sin C}\\ \text{cos 2A + cos 2B + cos 2C = -1 - 4 cos A}\text{.cos B}\text{.cos C}\\ \text{cos 2A + cos 2B + cos 2C = 1 - 2 cos A}\text{.cos B}\text{.cos C}\\ \text{sin A + sin B + sin C = 4 cos }\frac{\text{A}}{\text{2}}.\text{cos }\frac{\text{B}}{\text{2}}.\text{cos }\frac{\text{C}}{\text{2}}\\ \text{cos A + cos B + cos C = 1 + 4 sin }\frac{\text{A}}{\text{2}}.\text{sin }\frac{\text{B}}{\text{2}}.\text{sin }\frac{\text{C}}{\text{2}}\end{array}$$

There are some special half-angle formulas, double angle formulas, and triple angle formulas which help solve trigonometric functions, derivatives, and integration. 

Note that the above trigonometric identities are the modified versions of the identities that exist for any three angles. Only when angles A, B, and C are part of the same triangle, or if we can write A + B +C = π, only then these modified trigonometric identities can be used.

Laws of Sines

It states the relation between the sides of a triangle and the sine of its angle. If a, b, and c are sides of an oblique triangle, and $\angle A,\angle \text{B and }\angle \text{C}$are angles opposite to the sides a, b, and c respectively, then the law of sines can be given as:

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

Practice Problem

1. If Sin θ = 0.5, then find the value of cos θ.

⇒ We know, sin² θ + cos² θ = 1.

     If Sin θ = 0.5, then we can solve the problem as follows-

$$\begin{array}{l}{\text{sin}}^{\text{2}}{\text{θ + cos}}^{\text{2}}\text{θ = 1}\\ \Rightarrow {\left(\text{0}\text{.5}\right)}^{\text{2}}{\text{ + cos}}^{\text{2}}\text{θ = 1}\\ \Rightarrow {\text{cos}}^{\text{2}}\text{θ = 1 - }{\left(\text{0}\text{.5}\right)}^{\text{2}}\\ \Rightarrow {\text{cos}}^{\text{2}}\text{θ = 1 - 0}\text{.25}\\ \Rightarrow {\text{cos}}^{\text{2}}\text{θ = 0}\text{.75}\\ \Rightarrow \text{cos θ = }\pm \sqrt{\text{0}\text{.75}}\\ \Rightarrow \text{cos θ = }\pm \text{0}\text{.866}\end{array}$$

This is the required answer.

2. Write the double angle formula for tan x.

$\tan 2x=\frac{2\tan x}{1-{\tan }^{2}x}$

Context and Applications

Trigonometric identities form the base of trigonometry, and it is an important part of mathematics. For exams such as CSIR, NEET, GATE, IITJEE, ISI, CMI, and graduate-level entrance exams, ‘trigonometric identities’ is a very important topic.

• Bachelor of Science in Mathematics
• Master of Science in Mathematics