Why do we use scientific notation?
We have to deal with quantities that are extremely large or very small. For example- I may have 6,500,000,000 red blood cells, or the diameter of an iron atom is 0.000000011 inches. Numbers with many zeros can be inexpedient to work with, so scientists use scientific notation. It represents very large numbers or very small numbers in a simple form. We know that whole numbers can be extended to infinity, but we cannot write such large numbers on paper. Numbers that present in millions of places after the decimal point need to be represented simply. Thus, it is difficult to represent a few numbers in their extended form. Therefore, we use scientific notation.
Scientific notation
Scientific notation expresses very large or very small numbers concisely. Such numbers can be rewritten in standard form as a common number multiplied by 10 raised to a certain exponent or power.
Let us look first at large numbers. Suppose the distance between two satellites is 2,500,000 miles. The number 2,500,000 can be thought of as follows:
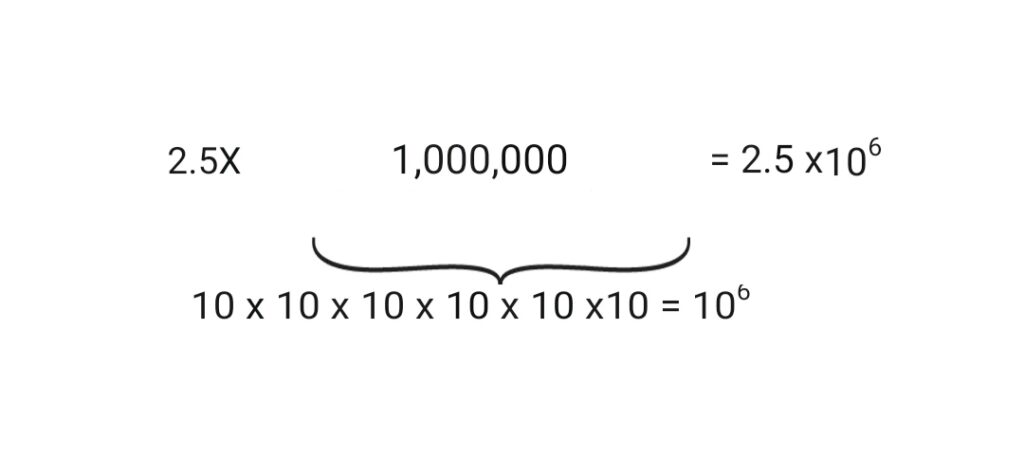
That is, 2,500,000 is the same as 2.5 times 1 million, and 1 million is 10 × 10 × 10 × 10 × 10 × 10, or 106 (which is read as “ten to the sixth power”). Therefore, 2,500,000 can be rewritten as 2.5 multiply with 106, or 2.5 × 106. The distance between two satellites can therefore be expressed as 2.5 × 106 miles.
The common rule for expressing numbers in scientific notation is a single non-zero first digit, a decimal place, and the rest of the numbers, excluding any trailing zeros. This number is followed by a multiplication sign and then raised by 10 to the power required to reproduce the original number. For example, 2,500,000 can also be written as 25 × 105 (which would be 25.0 multiply with 100,000), the convention is to have only one digit before the decimal point. The power is the number of places you have to move the decimal point to the left to make it follow the first digit.
So that the number is multiplied between 1 and 10 is 2,500,000 = 2.5 × 106.
We can use scientific notation to express the numbers whose magnitudes are less than 1. For example, the number 0.009 can be expressed as:
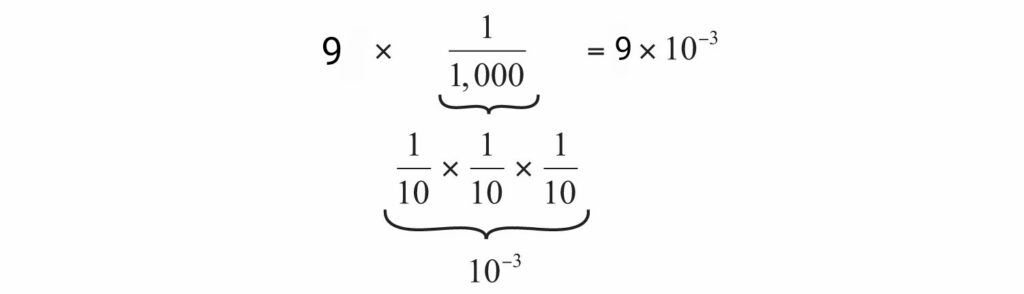
Positive and negative exponent
There are three parts in scientific notation; coefficient, base and exponent.
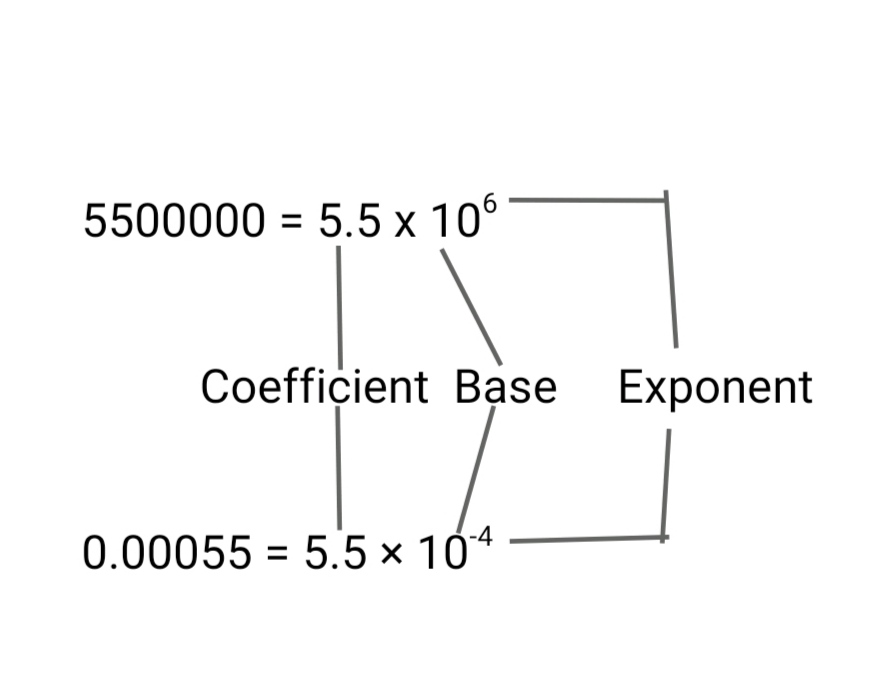
- When the scientific notation of any large numbers is expressed, then we use positive powers for base 10. Example:
10000 = 1 x 104, where 4 is the positive exponent. - When the scientific notation of any small numbers is expressed, then we use negative powers for base 10. Example:
0.0001 = 1 x 10-4, where -4 is the negative exponent. - From the above, we can say that the number greater than 1 can be written as the expression with a positive exponent, whereas the numbers that are less than 1 with a negative exponent.
Formulae
The general formula is:
- a × 10 b
- 1 ≤ a < 10
Rules
- The base should always be 10.
- Coefficients can be positive or negative numbers, including integers.
- Mantissa, i.e. the part of a number after the decimal point, carries the rest of the significant digits of numbers.
- The absolute value of the coefficient is greater than or equal to 1, but it should be less than 10.
- The indicator must be a non-zero integer, meaning it can be positive or negative
Units
Prefixes are commonly used in expressing a unit of measurement.
Prefix - Symbol - Factor - Meaning
- Yotta - Y - 1024 - septillion
- Yocto - y - 10-24 - septillionth
- Zetta - Z - 1021 - sextilltion
- Zepto - z - 10-21 - sextillionth
- Exa - E - 1018 - quintillion
- Atto - a - 10-18 - quintillionth
- Peta - P - 1015 - quadrillion
- Femto - f - 10-15 - quadrillionth
- Tera - T - 1012 - trillion
- Pico - p - 10-12 - trillionth
- Giga - G - 109 - billion
- Nano - n - 10-9 - billionth
- Mega - M - 106 - million
- Micro - µ - 10-6 - millionth
- Kilo - k - 103 - thousand
- Milli - m - 10-3 thousandth
- Hecto - h - 102 - hundred
- Centi - c - 10-2 - hundredth
- Deca - da - 101 - ten
- Deci - d - 10-1 - tenth
We use metric units for all our measurements; length will be measured in meters (m) or centimeters (cm), volume in centimeters (cm3), milliliters (mL), or liters (L), mass in grams (g) or kilograms (kg).
Calculators can show 8 to 10 digits in their display windows, which is not always enough when working with very large or very small numbers. For this reason, many calculators are designed to handle scientific notation. Many Calculators and computer programs use E to represent "times ten to the power of." Example: 2.05E20 means 2.05 × 1020. It is also referred to as E notation.
Engineering notation is very similar to scientific notation, except that the power of ten can only be a multiple of three. For example:
Arithmetic and scientific notation
Rules for Adding or Subtracting Two Numbers
- Rewrite the number with the smaller exponent so that it has the same exponent as the number with the greater exponent by moving the decimal point of its decimal number.
- Add/subtract the decimal numbers. The power of 10 will not change.
- Convert your result to scientific notation if necessary.
Example:
Addition
Add 6.7×104 + 3.87×105
First, notice that the exponents are 4 and 5. You will need to rewrite 6.7×104, so that it has an exponent of 5. Because you need to increase the exponent by 1, you will move the decimal point one space to the left.
6.7×104 converting into 0.67 × 105
Now, the problem is-
(0.67 × 105) + (3.87 × 105)
Next, add the decimal numbers. The power of 10 stays the same.
(0.67+3.87)×105
= 4.54 × 105
Finally, check if the answer is in scientific notation! 4.54 is at least 1 but less than 10.
The answer is
(6.7×104) + (3.87×105)= 4.54×105
Multiplication
Multiply/divide the powers of 10 by adding/subtracting their exponents.
Convert your answer to scientific notation if necessary.
Example:
(4.2 × 10−4)(6.5 × 108)
First, multiply the decimal numbers.
4.2×6.5 = 27.3
Next, multiply the powers of 10 by adding their exponents.
10-4 × 108 =10-4+8 =104
Now, combine the results.
(4.2 × 10−4)(6.5 × 108)
=(4.2×6.5)×(10-4 × 108)
= 27.3×104
Finally, convert your answer into scientific notation.
You will need to rewrite 27.3×104 so that the decimal number is at least 1 but less than 10. Move its decimal point one space to the left. Then, to keep the overall value the same, increase the exponent on the 10 by 1 such that 27.3×104 becomes 2.73×105.
The answer is 2.73 × 105.
Division
Divide (4.5 × 108) ÷ (2.5 × 10-4)
First, divide the decimal numbers.
4.5 ÷ 2.5 =1.8
Next, divide the powers of 10 by subtracting their exponents. Remember that subtracting a negative number is the same as adding the positive version of the number.
108 ÷10-4 = 108−(−4)= 108+4= 1012
Now, combine the results.
(4.5 × 108)÷(2.5 × 10-4)
=(4.5 ÷ 2.5)×(108 ÷10-4)
= 1.8×1012
Last, check to make sure that the answer is in scientific notation.
The calculation is 1.8×1012
Question yourself
1. Write each number in standard form.
a. 6.58 × 10−7
Answer- 0.000000658
b.1.506 × 10−4
Answer- 0.0001506
2. How to write 14 in scientific notation?
Answer- The scientific notation of 14 is:
1.4 × 101 = 1.4 × 10
Here,Coefficient = 1.4
Base = 10
Exponent = 1
Context and Application
This topic is significant in professional exams like
- Master of Science in Microbiology
- Bachelor of Science in Microbiology
- Master of Science in Physics
- Master of Science in Chemistry
Practice problems
Q 1. In engineering notation, the power on ten can only be a multiple of
- Two
- Four
- Three
- One
Answer: c
Explanation- In engineering notation, the power of ten can only be a multiple of three. So, three is the correct answer.
Q 2. What does 5.85E12 mean ?
- 12 times 10 to the power of 5.85
- 5.85 times 10 to the power of 12
- 5.85 times 12 to the power of 10
- 5.85 is multiplied by 12
Answer: c
Explanation- E represents “times ten to the power of.” So, the correct answer is 5.85 times 10 to the power of 12.
Q3. "Using scientific notation, 99 can be written as..........."
- 9.9 × 101
- 0.99 × 102
- 99 × 100
- 9.9 × 10-1
Answer: a
Explanation- The scientific notation of 99 is 9.9 × 101. Here,
Coefficient = 9.9
Base = 10
Exponent = 1
So, the correct answer is 9.9 × 10.
Q 4. Find the exponent number of 6.8 × 1015.
- 6.8
- 10
- 15
- 1015
Answer: c
Explanation- Exponent means the number of times a number is multiplied by itself. So, the correct answer is 15.
Q 5. Coefficient number of 1.67 × 10-7?
- -7
- 107
- 1.67
- 10-7
Answer: c
Explanation- Coefficient means a number used to multiply a variable. So, the correct answer is 1.67.
Related concepts
- Scientific calculator
- Engineering notation
- Positional notation
Want more help with your biology homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Scientific Notation Homework Questions from Fellow Students
Browse our recently answered Scientific Notation homework questions.