What is a crystal lattice and a unit cell?
Consider a crystal. The regular and repeating pattern of constituent particles is the most distinguishing feature of crystalline solids. A crystal lattice is formed when these particles are replaced with representative points. The three-dimensional arrangement of constituent particles is known as a crystal lattice. Unit cell is that the smallest portion of a space lattice which when repeated in several directions, generate the whole lattice. Unit cell is a building block of a lattice. It is the smallest unit of cell.
Solids are All Around
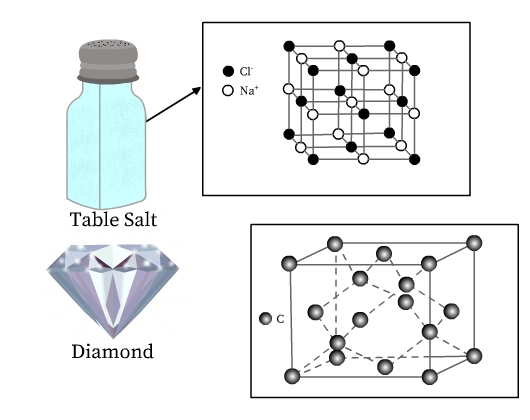
We know that solids are an indispensable part of our lives. Be it the table salt, the ice cubes in our refrigerator, the copper wires, or even the silverware and the diamonds—the list is long. We know that these materials have different properties and applications. Table salt is constituted of sodium and chloride ions, whereas ice is formed by binding of water molecules. Copper and silver are metals, whereas diamond is a network of carbon (a non-metal) atoms. It must be surprising that these substances have something in common—all are crystalline solids. Infact, the beautiful six-sided snowflakes are a result of the crystal structure of ice!
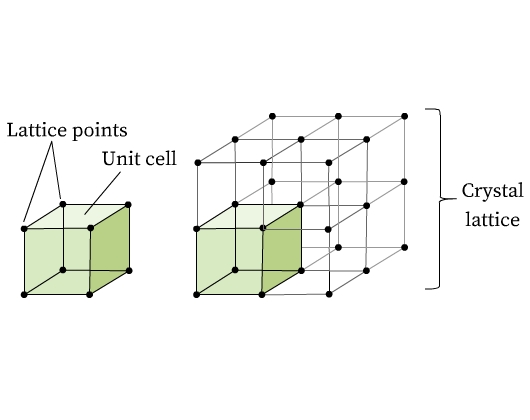
Imagine stacking of bricks in a wall (Fig 1). Every brick can be considered as a building block for the wall. Similarly, a crystalline solid is composed of identical units (bricks) that periodically repeat throughout the solid forming a three dimensional regular structure called crystal lattice (wall). These small repeating units in a crystal lattice are called unit cells. Unit cells are composed of one or more atoms, molecules, or ions, which are represented by points in the lattice structure, called lattice points. Fig 2 shows lattice points and the formation of a crystal lattice from unit cells.

See Fig 3 for structure of table salt and diamond. Both table salt and diamond have a regular arrangement of their constituent particles. Unit cell of table salt is composed of sodium and chloride ions, and that of diamond is made up of carbon atoms (Fig 2), which are represented as lattice points in their respective crystal lattices.
Crystal Lattices
Structural Motifs
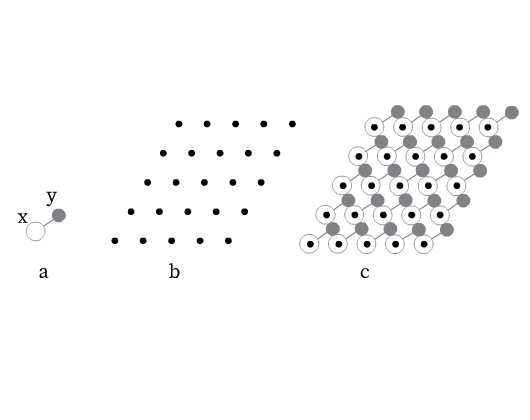
A periodic crystal structure contains regularly repeating ‘basis’ or ‘structural motifs’ that generate the three-dimensional crystal structure. These structural motifs may be an atom, a molecule or an ion, or a group of atoms, molecules, or ions. For example, the structural motif for NaCl would be one sodium ion and one chloride ion. Fig 4a shows a structural motif formed by an X and Y atom.
Lattice Point and Space Lattice
Consider placing a single point in each repeated structural motif at the same location. The pattern so formed is called as space lattice (Fig 4b). These points are lattice points that represent the position of an atom, molecule or ion, or a group of atoms, molecules, or ions in a space lattice. A space lattice can thus be defined as the pattern formed by lattice points representing the locations of atoms, ions, or molecules (structural motifs) in 3-D space.
It is important to note here that crystal structure is different from space lattice. Crystal structure is obtained by positioning an identical structural motif at each lattice point (Fig 4c).
Unit Cells
Consider joining neighboring lattice points with straight lines as shown in Fig 5, forming a parallelepiped (a parallelepiped is a six-sided figure, each side of which is a parallelogram).
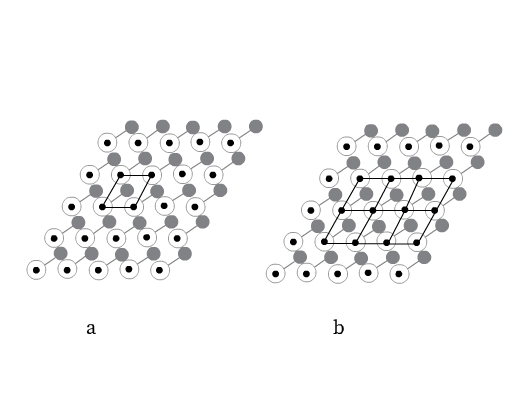
The crystal structure can be divided into such identical series of parallelepipeds (Fig 5b). Each such parallelepiped is called unit cell. This parallelepiped is a complete unit from which the entire crystal can be generated by translation (stacking), like bricks form a wall. A crystal may be considered to be composed of an infinite number of such unit cells. Unit cell can thus be defined as an imaginary parallelepiped from which the entire periodic crystal can be generated by using only translations.
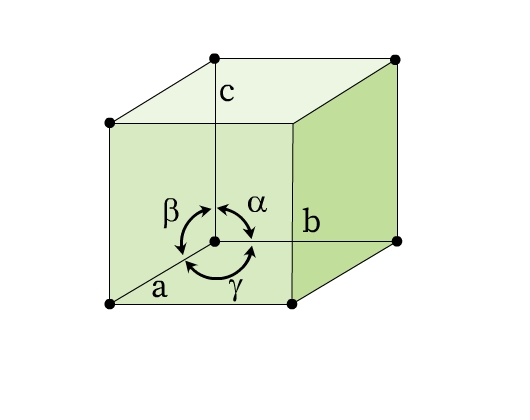
The lengths of the edges of a unit cell (a, b, c) and the angles between these edges (α, β, ϒ) are called lattice parameters or unit cell parameters (Fig 6).
Types of Unit Cells
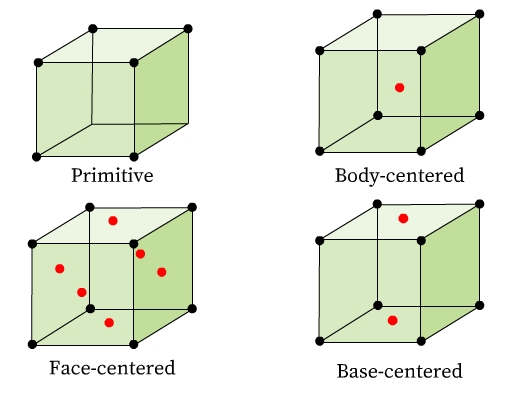
Unit cells can be broadly classified into two categories (Fig 7):
- Primitive Unit Cells (P): Constituent particles occupy only the corner positions of the unit cell.
- Centered Unit Cells: One or more constituent particles is /are present at positions other than corners of the unit cell. There are three types of centered unit cells:
(1) Body-Centered Unit Cells (I): It consists of a constituent particle in the center and others occupy its corners.
(2) Face-Centered Unit Cells (F): It consists of a constituent particle at the center of each face and others occupy its corners.
(3) Base-Centered (or End-Centered) Unit Cells (C): It consists of a constituent particle present at the centers of any two parallel faces and others occupy its corners.
Let us now focus on understanding the arrangements understanding the arrangements in cubic crystal system resulting in these three dimensional structures.
Close Packed Cubic Crystals
Close Packing in Two Dimensions
Consider you have a few marbles. How can you arrange them in one layer on a plane? They must be in contact so that they occupy the minimum space. This arrangement can be done in two ways as shown in Fig 8.
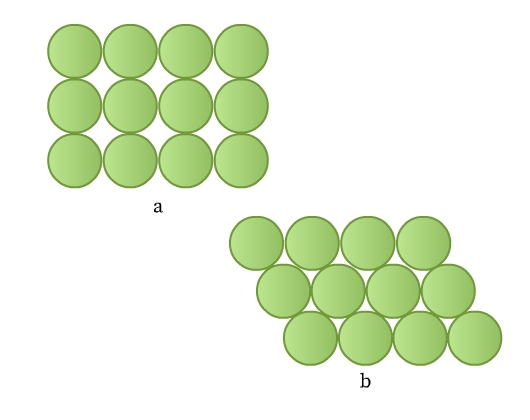
The constituent particles in crystals can be considered as identical hard spheres similar to the marbles. These can be arranged in a two-dimensional array in two ways:
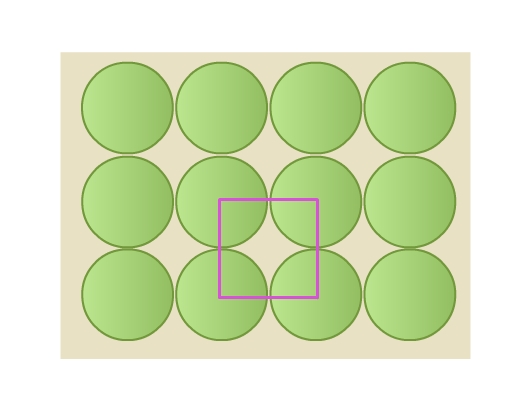
- Rows are aligned exactly above and below each other (Fig 8a). Each sphere is in contact with four of its neighbors. This packing is called square close packing. Joining the centers of these four spheres gives a square (Fig 9).
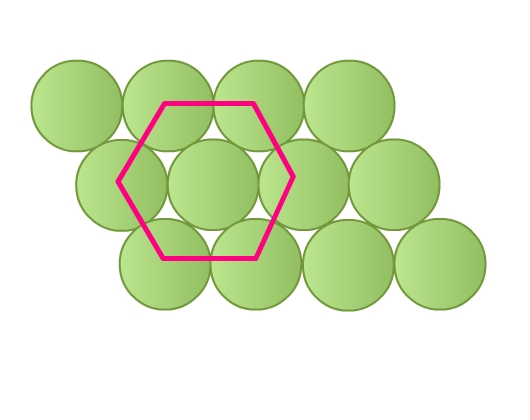
- Rows are aligned such that spheres of a row are placed in depressions of the previous row (Fig 8b). Each sphere is in contact with six of its neighbours. This packing is called hexagonal close packing. Joining the centers of these six spheres gives a hexagon (Fig 10). This packing is more efficient than the square close packing.
Close Packing in Three Dimensions
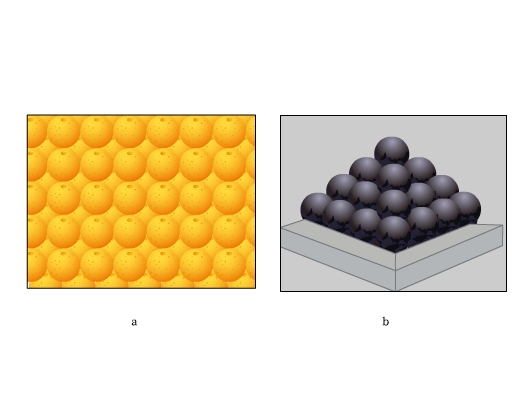
Have you ever closely seen the stacking of fruits on a market stall? Or noticed the arrangement of canon balls? See the figure below. These arrangements are highly efficient. We find the constituent particles in many crystals arranging themselves in these patterns. Let us find how.
Three dimensional structures can be obtained by stacking two dimensional layers.
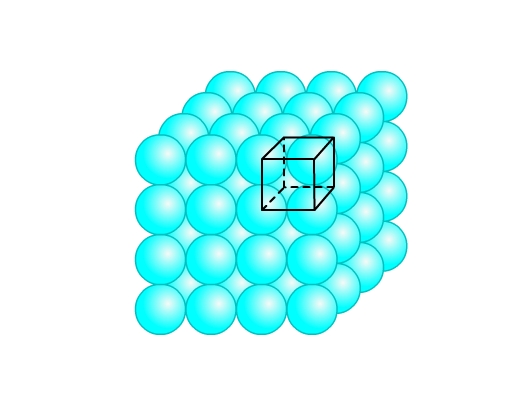
- Simple cubic lattice: This packing is obtained from two dimensional square close packing (Fig 9) by placing a second layer over its first layer such that the spheres are exactly on top of the spheres below. Similarly, more layers can be placed. All layers are identical, and let’s say are of ‘A’ type. Thus, we call it AAA type of arrangement. The lattice so generated is the simple cubic lattice (Fig 12). Each sphere is in contact with four spheres in its own layer, one above and one below. Hence, coordination number is 6. This structure occupies only 52% of the space. Po crystalizes in this form.
- Hexagonal close packed structure (hcp): This packing is obtained from two dimensional hexagonal close packing (Fig 10). Place a second layer over the voids of its first layer. The second row is ‘B’ type as it is different from the first one (Fig 13). A tetrahedral hole is formed where a sphere of second layer is above the void of the first layer. This hole constitutes three spheres from the lower and one from the upper layer. On joining the centers of these four spheres, a tetrahedron is formed. If a third layer is now placed over the second, such that it covers the tetrahedral holes, it is exactly over the first layer. Similarly, fourth layer aligns with second. This pattern is therefore ABAB type called hexagonal close packed (hcp) structure. Metals like Be, Mg, Co, Zn, Ti have hcp structures.

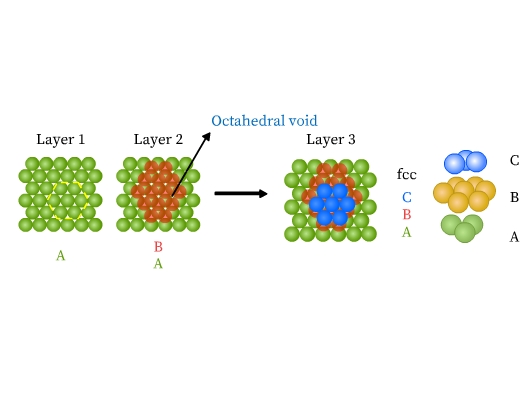
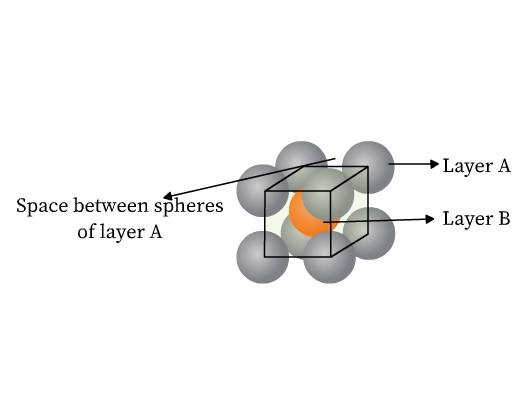
- Face centered cubic (fcc) or cubic close packed (ccp) structure: This type of packing is also obtained from two dimensional hexagonal close packing. Note that where the triangular voids of second layer are over the triangular voids of first layer, an octahedral hole is formed (Fig 14). This void constitutes of three spheres from the lower and three in the upper layer. On joining the centers of these six spheres, an octahedron is formed. If a third layer is placed over the second, such that it covers the octahedral holes, it aligns neither with the first nor with the second layer. This layer is thus ‘C’ type. When fourth layer is placed, it aligns with the first. This pattern is therefore ABCABC type (Fig 14). This structure is called face centered cubic (fcc). Metals like Al, Cu, Pb, Au, and ionic crystals like NaCl, LiH, MgO crystallize in this form.
In both hcp and fcc, coordination number is 12. A sphere is in contact with six spheres in its own layer, three spheres each in the layer above and below. Both hcp and ccp are highly efficient and fill 74% of the space. If you notice, these are the arrangements we find stacking of fruits and canons.
- Body centered cubic (bcc): This packing has spheres in the first layer (type A) slightly separated and the second layer (type B) is placed in the depressions between the spheres of the first layer (Fig 15). The third layer aligns with the first. Hence, it is a ABAB type arrangement, with coordination number for each sphere being 8—four neighbours each in layer above and below. This structure occupies only 68% of the space. Examples of metals having bcc structure include Cr, Mo, Ba, K, Cs.
Practice Problems
Q1. Repeating unit of a crystal lattice is known as:
- Lattice point
- Constituent atom
- Basic
- Unit cell
Answer: Unit Cell
Q2. What will be the structural motif for potassium bromide crystal?
- Potassium ion
- Bromide ion
- Potassium ion and bromide ion
- Potassium and bromine atoms
Answer: Potassium ion and bromide ion
Q3. Which unit cell consists of constituent particles at the corners and in the center?
- Primitive
- Body-centered
- Face-centered
- Base-centered
Answer: Body-centered
Q4. Barium has a body centered cubic structure. What will be the coordination number for each potassium ion?
- 8
- 12
- 6
- 10
Answer: 8
Q5. Which of the following lattice consists of octahedral voids?
- Simple cubic
- Face centered cubic
- Body centered cubic
- All of these
Answer: Face centered cubic
Context and Applications
Crystal lattices and unit cells are studied under crystallography. Knowledge of unit cells helps in accurately evaluating the structure of a solid. You will study these in your higher studies in Chemistry. This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
Bachelors of Science in Chemistry
Masters of Science in Chemistry
Want more help with your chemistry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Crystal Lattices and Unit Cell Homework Questions from Fellow Students
Browse our recently answered Crystal Lattices and Unit Cell homework questions.