What is Valence Bond Theory?
Valence bond theory (VBT) in simple terms explains how individual atomic orbitals with an unpaired electron each, come close to each other and overlap to form a molecular orbital giving a covalent bond. It gives a quantum mechanical approach to the formation of covalent bonds with the help of wavefunctions using attractive and repulsive energies when two atoms are brought from infinity to their internuclear distance.
History and Background
Linus Pauling and John C. Slater were the two scientists to put forward VBT in 1927. They were able to explain the stability of covalent bonding in hydrogen molecule by utilizing the Schrodinger wave equation and specific wave functions for each individual atom and how they join to form a molecule.
VBT theory has served as one of the basic theories of chemical bonding to understand covalent bonding in molecules.
Understanding VBT via the Formation of the Hydrogen Molecule
To understand the covalent bonding in H2 molecule, consider two hydrogen atoms with nuclei A and B respectively. Let us take the electrons in the atoms to be e1 and e2.
we can represent the whole atoms as and .Wavefunctions corresponding to electrons in separated atoms can be represented as and . is then, also the wavefunction for the atomic orbital of hydrogen atom containing first electron and represents the wavefunction of the atomic orbital of hydrogen atom containing second electron.
Let’s assume both the hydrogen atoms now have no interaction between them and are separated by an infinite distance. As they approach and come closer to each other, the nucleus of the first atom HA might attract the electron of the second atom. Similarly, the second atom’s nucleus HB will have attractive forces for the first hydrogen atom’s electron. When they approach closer and closer there is also going to be an increase in the repulsive forces between the nuclei HA and HB , as well as e1 and e2. Based on the strength of these attractive and repulsive forces, the formation of the bond and its energy can be determined.
To understand this through the graph, we can first represent the internuclear distance with rAB. Plotting rAB against the energy of the molecule we get a graph as shown below.
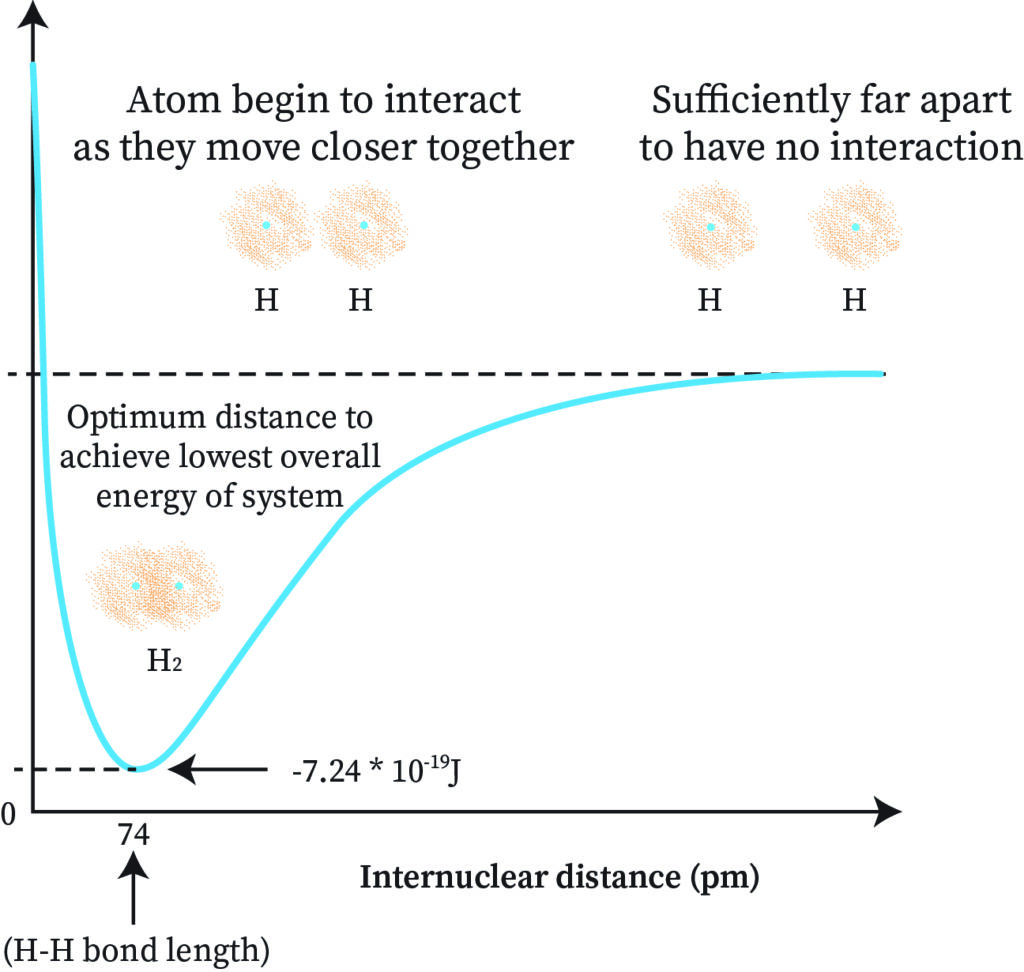
The rAB distance where the energy is minimum is the covalent bond distance between the atoms. When energy is the lowest, stability is high and the rAB distance corresponding to that gives the bond length which is how the formation of H2 takes place. A hydrogen-hydrogen sigma bond (sigma bond) is formed here.
Experimental and theoretical observation on energy
In order to calculate the energy during the variation of internuclear distance rAB, we can use the energy equation or Hamiltonian equation from quantum mechanics. It was observed that the experimental energy obtained from the curve was found to be 458kJ/mol whereas the bonding energy obtained theoretically was found to be just24kJ/mol . This disagreement in the value was observed due to the fact that we neglected other interactions possible between the two hydrogen atoms (HA(e1)and(HB(e2 ). There are three such main interactions that cause a change in binding energy.
Other Interactions between hydrogen atoms
Exchange of electrons
The earlier approach assumed that the electrons belonging to both the atoms are distinguishable from each other, which is why they were represented differently as e1and e2. But in reality, these electrons are indistinguishable from each other, hence there will be an exchange of electrons between the nucleus of both atoms HA and HB.
This naturally results in the formation of two states such as HA(e1)HB(e2 ) and HA(e2)HB(e1 ). Therefore these states will eventually have two wavefunctions as well which
are and .
So as to find the total energy linear combination of these two wavefunctions must occur and there are two ways in which these two wavefunctions can combine linearly which are additive and subtractive combination.
Additive combination can be represented as Ψ+.
Similarly, subtractive combination can be represented as Ψ-.
Though the two states are possible for hydrogen molecules, Ψ+the state is known as the bonding state. Only when it is Ψ+, there is a covalent bond formation between the hydrogen atoms. Whereas the Ψ- gives the repulsive state, where bonding does not take place between hydrogen molecules due to high energy and less stability, therefore hydrogen molecule does not get formed.
Exchange energy contributes up to a total of 279kJ/mol in hydrogen molecule in addition to the bonding energy already calculated from the Hamiltonian equation mentioned above.
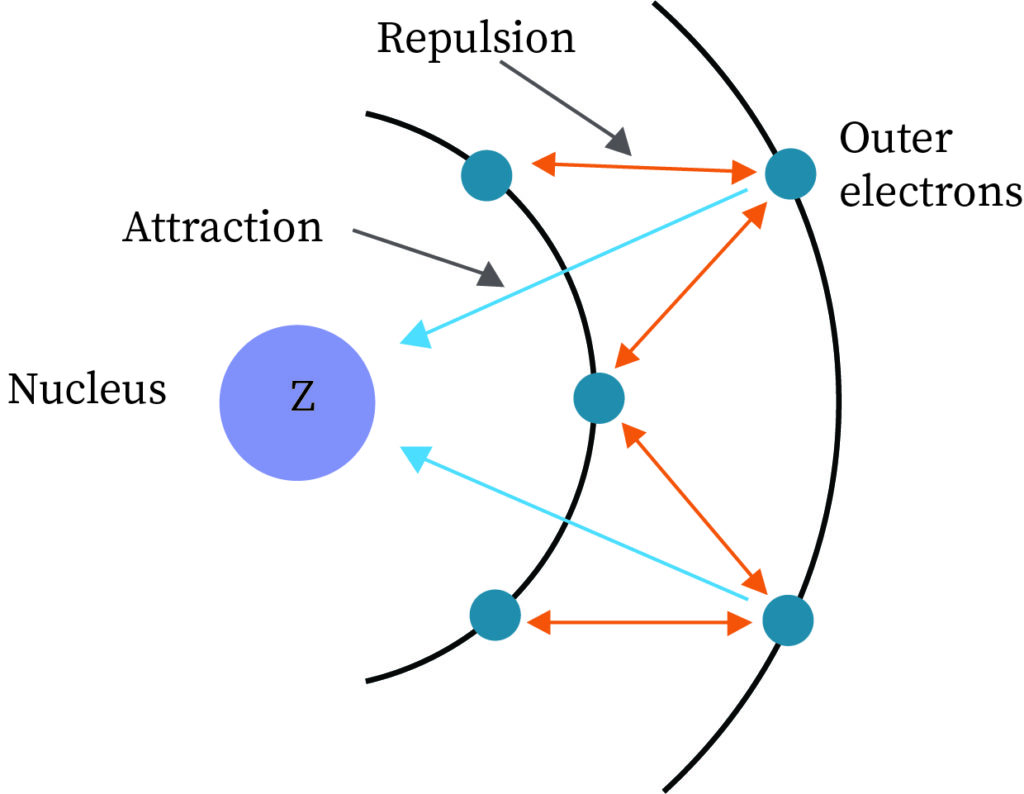
Screening effect of electrons
When two atoms approach close to each other the electron of one atom tends to shield the electron of another atom. This disables the electron from another atom to experience the full charge exerted by the nucleus of the other atom. This resultant charge experienced by the other electron is termed as an effective nuclear charge which is less than the actual charge that the nucleus exerts. This contributes to some energy in the bond formation of H2 in addition to that obtained theoretically.
Ionic character of hydrogen bond
There could be a possibility that both the electrons are close to one nucleus or the other simultaneously at one point during the bond formation. This may lead to the formation of ionic states.
Possibilities such as ( )and () , can be represented as and ionic states respectively. These will in return have separate wavefunctions () and their linear combination results in the total wavefunction corresponding to the ionic part of hydrogen bond.
This does not mean that the bond is fully ionic, that is a very wrong concept to say, as hydrogen bond is evidently covalently bonded, because there is very little contribution from the ionic nature in comparison to that of covalent nature. Thus, the overall wavefunction can be expressed as
Where λ is mixing coefficient, which gives information about the extent to which ionic nature occurs in the H-H bond. This contribution to energy is also added along the bonding energy of 24kJ/mol found theoretically.
Valence Bond Theory and Molecular Orbital Theory
In valence bond theory chemical bonds between two atoms have been accomplished by the combination of two orbitals. According to molecular orbital theory (MOT), atomic orbitals of the atoms in a molecule will combine to form molecular orbitals. In valence bond theory only bonding interactions were considered. Molecular orbital theory considered both bonding and anti-bonding orbitals. Valence bond theory explains the hybridization concept which involves the s-orbitals p-orbitals and d-orbitals.
Common Mistakes
Always remember VB Theory is a quantum mechanical approach to chemical bonding not classic as it explains the wave nature of electrons.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for Chemistry.
Want more help with your chemistry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Valence Bond Theory Vbt Homework Questions from Fellow Students
Browse our recently answered Valence Bond Theory Vbt homework questions.