What is Angular Momentum? 

The momentum of an object is given by multiplying its mass and velocity. Momentum is a property of any object that moves with mass. The only difference between angular momentum and linear momentum is that angular momentum deals with moving or spinning objects. A moving particle's linear momentum can be thought of as a measure of its linear motion. The force is proportional to the rate of change of linear momentum. Angular momentum is always directly proportional to mass. In rotational motion, the concept of angular momentum is often used. Since it is a conserved quantity—the total angular momentum of a closed system remains constant—it is a significant quantity in physics. To understand the concept of angular momentum first we need to understand a rigid body and its movement, a position vector that is used to specify the position of particles in space. A rigid body possesses motion it may be linear or rotational. Rotational motion plays important role in angular momentum. 

Rigid Body 

Any real body that we come into contact with, on a daily basis has a finite size. Any material or body made up of a large number of point size particles is said to be rigid if its shape or size does not change over time, during motion, or when subjected to an external force. A rigid body is typically thought of as a continuous mass distribution. A rigid body's location is the position of all the particles that make it up. 

A rigid body's location has two components: linear and angular. When a rigid body moves, the location of the body change over time. It possesses velocity as the body is displaced through some distance. Under the impact of external forces, the relative locations of the particles of the body remain unchanged. 

The concept of angular momentum of a rigid body can be explained with the help of examples like, planets that have angular momentum as a product of their rotation and orbits around stars. In engineering, something that rotates around an axis, such as flywheels, propellers, and revolving parts in engines, has angular momentum. 

Position Vector 

A position vector is a straight line with one end attached to a body and the other to a moving point that is used to define the position of the point in relation to the body. Let us consider a position vector r in following figure. A body of mass m is located at point A (x, y, z). 

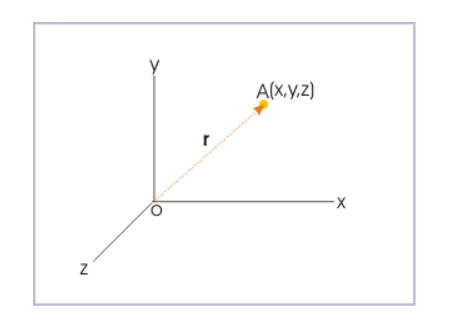
Rotational Motion 

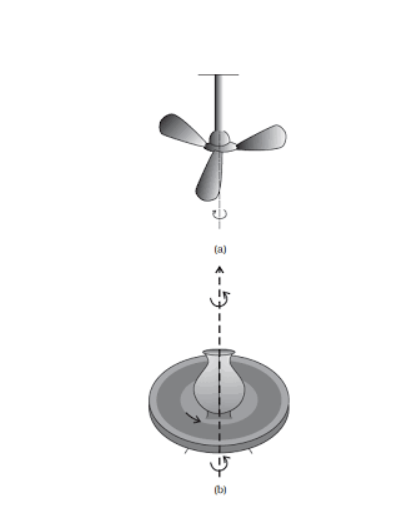
If any particle in the body moves in a circle around a single line, this is known as pure rotational motion. The axis of rotation is the name given to this line. The general motion of a rigid body tumbling through space can be defined as a combination of translation and rotation around an axis through the body's Centre of mass. Many examples of rotation around an axis can be found around you, such as a ceiling fan (shown in the figure below), a potter's wheel, a giant wheel at a fair, and so on. 

Linear Momentum

Linear Momentum is given by the product of velocity of a body and its mass. 

The linear momentum of a mass m body and velocity v is equal to p=mv 

When the mass is measured in kilograms and the velocity is measured in meters per second, the momentum is measured in kilogram meter per second (kgm/s). Momentum has magnitude and direction since it is a vector. 

The number, angular momentum, is the rotational equivalent of linear momentum, just as the moment of a force is the rotational analog of force. Angular momentum, like the moment of a force, is represented by a vector product. It is also called the moment of (linear) momentum. 

Angular Momentum 

Angular Momentum (represented by L) of an object is the moment of linear momentum. It is also the product of angular velocity and moment of inertia of any object. 

The angular momentum of a particle is defined as the cross-product of $\overrightarrow{r}$ and $\overrightarrow{p}$

is perpendicular to the plane containing $\overrightarrow{r}$ and $\overrightarrow{p}$

$L=\overrightarrow{r}\times \overrightarrow{p}$

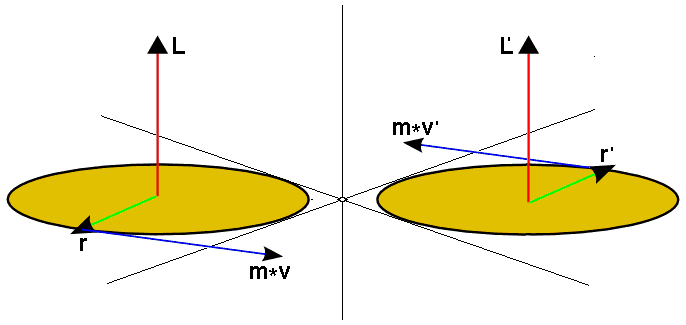
Angular Momentum for a Single Particle 

Figure shows a particle with linear momentum $\overrightarrow{p}=m\overrightarrow{v}$ with respect to the origin at a position $\overrightarrow{r}$. We may describe an angular momentum in terms of the position vector and the linear momentum even if the particle is not rotating around the origin.

Right-Hand Rule 

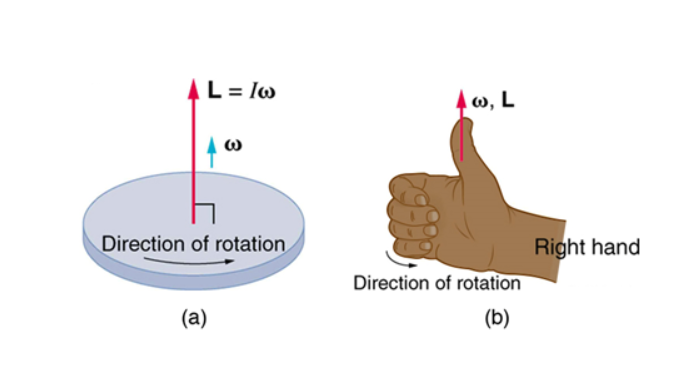
The right-hand rule defines the direction of angular momentum as follows: 

If you place your right hand in such a way that the fingers are pointing in the direction of r. Then, with them curled around your hand, point in the direction of linear momentum (p). The direction of angular momentum is indicated by the outstretched thumb (L). 

It implies that, based on the equation, the magnitude of angular momentum can be determined using the cross-product concept.  

$L=rpsin\theta$

where the angle between $\overrightarrow{r}$ and p is θ. The units of angular momentum are kg⋅m2/s

Angular Momentum of a System of Particles 

Many scientific disciplines, including astronomy, depend on the angular momentum of a system of particles. We discussed the angular momentum of a single particle around a given origin in the previous section. 

This angular momentum is expressed as $L=\overrightarrow{r}\times \overrightarrow{p}$ where the vector $\overrightarrow{r}$ is from the origin to the particle and $\overrightarrow{p}$ is the particle’s linear momentum. If we have a system of N particles, each with position vector from the origin given by $\overrightarrow{r}$ and each having momentum $\overrightarrow{p}$ then the total angular momentum of the system of particles about the origin can be found by the vector sum of the single angular moments. That is.

$\overrightarrow{L}=\overrightarrow{l_1}+\overrightarrow{l_2}+\mathrm{....}+\overrightarrow{l_N}$

Angular Momentum & Torque 

Torque, like force, is known as the rate of change of angular momentum. The total torque on any device is always equal to the total external torque. 

Given, the linear momentum of a particle is $\overrightarrow{p}=m\overrightarrow{v}$and its position vector is $\overrightarrow{r}$, then

angular momentum can be written as  
L = r×p = m(r×v)   (1) 

Angular momentum is a vector quantity, and its direction is perpendicular to the direction of r and p and could be found out by right hand screw rule. 

From equation 1 angular momentum magnitude can be written as 
|L|=rpsinθ                  (2) 

Differentiating equation L w.r.t. t we get 

$\begin{array}{c}\frac{dL}{dt}=\frac{d\left(r\times p\right)}{dt}=\left(\frac{dr}{dt}\times p\right)+\left(r\times \frac{dp}{dt}\right)\\ \text{but }\frac{dr}{dt}=v\text{ and }p=mv\\ \left(\frac{dr}{dt}\times p\right)=v\times mv\\ =m\left(v\times v\right)\\ =0\\ \text{So,}\frac{dL}{dt}=\left(r\times \frac{dp}{dt}\right)\end{array}$

But from newton's second law of motion, we have 

$\begin{array}{c}\frac{dp}{dt}=F\\ \frac{dL}{dt}=\left(r\times F\right)\\ r\times F=\tau \text{ (torque)}\\ \frac{dL}{dt}=\tau \end{array}$

Hence rate of change of angular momentum with time is equal to the torque of the force. 

_{Angular Momentum & Moment of Inertia} 

To find the angular momentum of an object, consider the rigid object rotating about z axis, (as shown in the Figure).  The individual particles of the object are considered to be rotating about z axis with angular ω.  

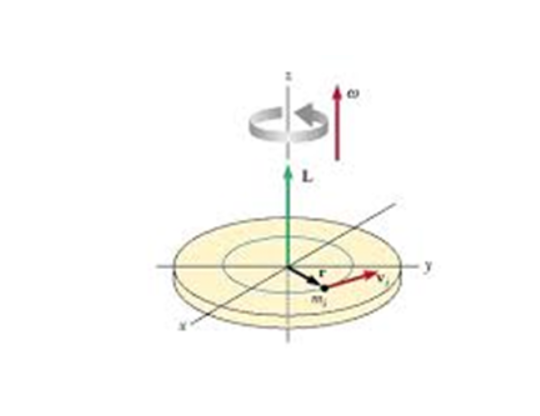
The magnitude of the angular momentum, of a particle of mass m_i about the z axis is 

l_i = m_i v_ir_i. Now we have v_i = r_iω, thus angular momentum can be re-written as 

l_i = m_ir_i²ω 

This angular momentum for the i^th particle is also along the z-axis. Thus the angular momentum of the entire object is found by summing up each term, 

$$\begin{array}{l}{L}_{net}=\omega {\displaystyle \sum _{i=1}^n\begin{array}{l}\\ \end{array}}{m}_i{r}_i{}^2\\ =I\omega \end{array}$$

Here, I= ∑ m_ir_i², is the moment of inertia of the object about the z axis.

Example of Angular Momentum 

Ice-skater 

As an ice skater begins a spin, she holds her hands and legs far away from her body's middle. When she wants more angular momentum to spin, on the other hand, she brings her hands and legs closer to her body. As a result, she conserves angular momentum and spins faster. 

Common Mistakes 

• Many people believe that any external force acting on a device can cause angular momentum to change. A net external torque changes angular momentum, but not all forces produce a torque. 
• Another common misunderstanding is that the torques at the fulcrum only add up to zero. The torques on an object in equilibrium sum to zero around either axis. 

Context & Applications 

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for 

• 10th,11th,12th Standard. 
• Engineering Students. 
• Angular momentum is useful in motorcycle and bicycle dynamics, 
• Aircraft flight stability control 
• Mobile electronic system gravity sensing. 

Related Concepts

• Conservation of angular momentum 
• Rigid body & circular motion 
• Centre of mass 
• Kinematics of rotational motion 
• Conservation of angular momentum 
• Dynamics of rotational motion