What is Angular Position?
Before diving into angular position, one should understand the basics of position and its importance along with usage in day-to-day life. When one talks of position, it’s always relative with respect to some other object. For example, position of earth with respect to sun, position of school with respect to house, etc. Angular position is the rotational analogue of linear position.
In straight line motion, the position is with respect to a fixed point, and distance displacement is given with respect to that position. In terms of the X-Y plane, the position is defined as change in either X or Y or both, and change of position with respect to time is called speed.
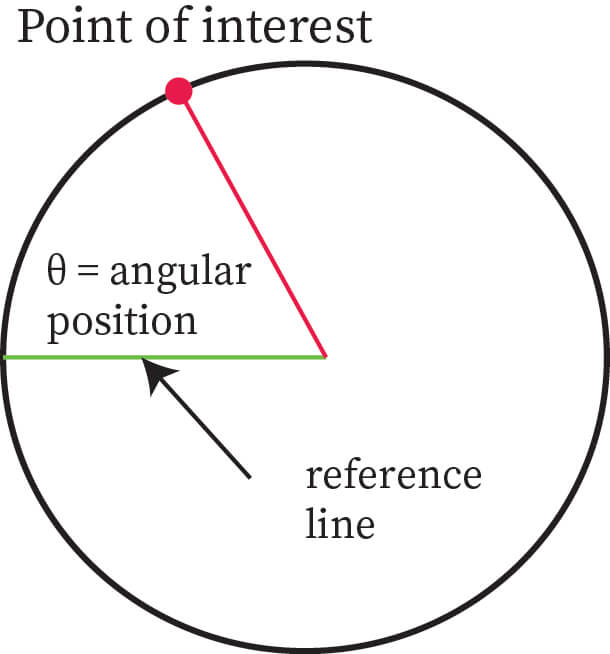
When a body moves in a circle, the position of the body at any point of time is given in terms of angle it has moved with respect to reference or start point. From figure 2, the point can be seen at an angle of θ with a reference line. This is known as angular position.
Concept
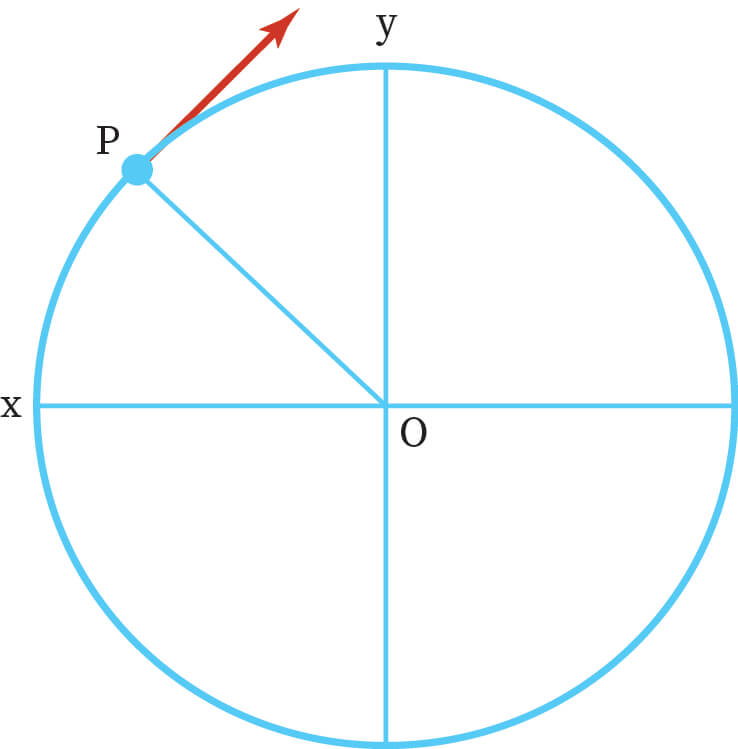
In angular motion, motion of particles is considered about the circle, and the X-Y plane is super positioned over it as shown in figure 3. One diameter of the circle is measured along the x-axis, and another is measured along the y-axis, such that both the diameters are perpendicular to each other, as seen in Figure 3. At point P, an object of mass ‘m’ travelling with velocity v is considered. Before we get into the details of angular motion, it's essential to know the difference regarding positive and negative rotation. The clockwise motion is assumed as negative and anti-clockwise is considered to be positive.
It may very well have been observed that the particle's positioning is determined by the angle formed by the line between the particle and the origin, which is referred to as angular position or angular displacement. When we talk about angular displacement, the angle can be either clockwise or anticlockwise, but when we talk about angular distance, we ignore the angular direction and instead reflect on the magnitude. Needless to say, angular displacement is a vector quantity. Angular displacement further is used to get various parameters such as angular velocity, angular acceleration. The angular displacement is defined as the shortest angle between the initial and final positions for a given particle undergoing circular motion around a fixed point. The unit is radians.
Formula for angular displacement
Angular displacement=
We know that,
Where= the angular displacement of the particle
= distance moved on the circle by the particle
= radius of the circle.
Problem:
Question: Racer runs around a circular track of 49 m radius. He covers a distance of 312 m. Calculate the angular displacement of the runner.
Answer:
The distance covered by the racer is, = 312 m
Radius of the track is, = 49 m.
Using formula for angular displacement,
Application
Angular Velocity
It has a similar linear velocity. Linear velocity is defined as the rate of change of linear displacement. Similarly angular displacement can be defined as rate of change of angular displacement with respect to time. It is denoted by (Omega). It is given by the following expression.
Here, is the final angular position,
is the initial angular position and is the total time interval.
The above expression gives the average angular velocity. For finding the instantaneous angular velocity we can use the below expression.
When the time interval approaches zero, we get the instantaneous velocity.
Note
The right-hand rule defines the direction of angular velocity: curl your right hand's fingers in the direction of rotation, leaving the thumb straight along the axis here z-axis perpendicular to the plane of rotation (here XY-plane), and the thumb determines the direction. For example, When the particle is going in an anticlockwise direction, curl the right-hand fingers in an anticlockwise direction, leave the thumb straight (here along the z-axis), and the thumb gives the angular velocity direction.
Angular Acceleration
Similar to the case of linear acceleration, in circular motion we have angular acceleration. The rate of change of angular velocity with respect to time is angular acceleration. It is denoted by (alpha).
To get instantaneous angular velocity, time approaches to zero.
Note:
To get the direction of angular acceleration, if the angular velocity is increasing, it’s in the same direction that of angular velocity but if the angular velocity is decreasing then angular acceleration is in opposite to the direction of angular velocity.
Relation between Angular speed and linear speed
From definition of angular position, we know that,
On differentiating with respect to time we have
Where gives the linear speed, and gives the angular velocity.
∴ we have , it represents linear speed in terms of angular speed and vice versa.
Centripetal Acceleration in terms of angular velocity is given by the below expression.
Tangential Acceleration is given by the differentiation, with respect to time,
We get
Note
Acceleration can be there even if the velocity is constant, this is due to change in direction of velocity. Hence, we can conclude that acceleration can be there due to change in direction or magnitude or both.
The acceleration generated in a particle moving in uniform circular motion, as a result of total external force exerted on the particle is known as centripetal acceleration. Its direction is towards the center. For example, cars experience centripetal acceleration when it turns. Here the friction provides necessary force required.
Some other examples are, banking on roads, bending of cycle or bikes at steep turns.
Tangential acceleration is measured to get change in tangential velocity at a point with a given radius.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science in Physics
- Master of Science in Physics
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Angular Position Homework Questions from Fellow Students
Browse our recently answered Angular Position homework questions.