What are Atomic Spectra?
According to the Bohr model of an atom, the electron in an atom moves around a nucleus in fixed orbits with specific energies known as energy levels. The orbital energies are quantized. The electrons remain in these energy levels until they emit or absorb a photon of a particular wavelength, the quantum of energy. If the electron emits a photon, it then falls back to a lower energy level, and if it absorbs a photon, the electron rises to higher energy levels. The photons released or absorbed in these transitions of an electron are studied and analyzed on a screen as atomic spectra.
Types of spectrum
The atomic spectra can be categorized into two categories, Emission spectrum, and Absorption spectrum.
Emission spectra
The emission spectra of a chemical compound or element are the frequency spectra emitted when an atom transitions from a high energy state to a low energy state. In this process, a photon is emitted. According to the conservation of energy, the energy of an emitted photon is equal to the energy difference between the energies of two states. There are several possible transitions for each atom, with each transition, having a specific energy difference. For such transitions, these atoms and molecules emit radiations at different wavelengths of corresponding photons. The emission spectra of each atom are unique. This quality can be used to identify elements in a matter whose composition is unknown. If the material emits dense wavelengths in a broad range then it is known as a continuous spectrum. In few cases, atoms emit light of a certain wavelength like a line which is known as a discrete emission spectrum.

Absorption spectra
The absorption atomic spectra of an atom are the fraction of incident radiation that is absorbed by it over a range of frequencies or equivalently wavelengths. When a photon with specific energies that match the energy difference between any two allowed energy levels (frequency/wavelength) is incident on an atom, the electrons in that atom can absorb and get promoted to higher energy levels. The direction of re-emitted light and that of the absorbed photon is unlikely to be the same. The missing wavelength in these spectrum appears as darker lines or bands.
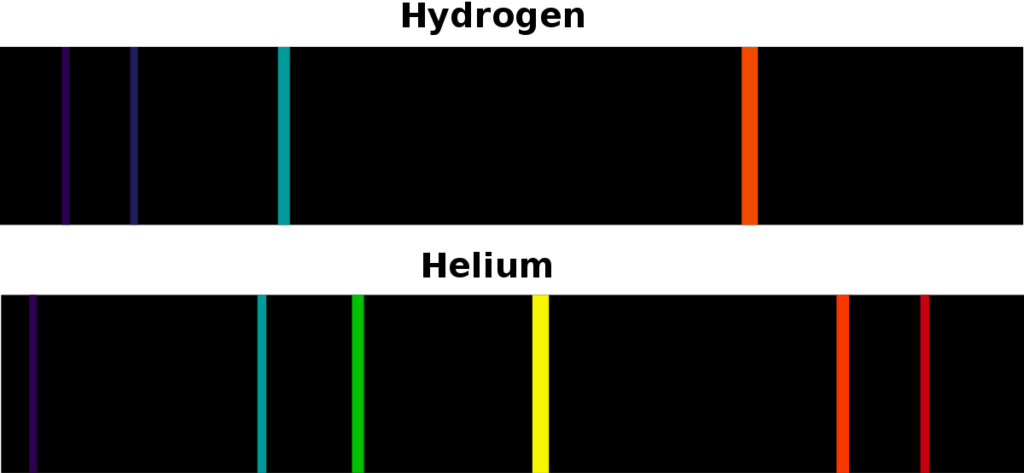
Spectral lines in the Hydrogen atom
The solution to Schrodinger's equation in the case of the Hydrogen atom can be separated into radial and angular parts, as,
Where,
is the total hydrogen wavefunction,
R is the radial part of the hydrogen wavefunction, it is characterized by principal quantum number n which goes from n=0, 1, 2, ........
is the polar part of the hydrogen wavefunction, it is characterized by orbital quantum number l, it varies from l=0, 1, 2 ....... n-1,
is the azimuthal part of the hydrogen wavefunction, it is characterized by the magnetic quantum number m and it m=0, ±1, ±2 ........ ±l
If we ignore the spin-orbit interaction and relativistic corrections to the energy of the hydrogen atom. Its energy depends only upon the principal quantum number. The magnitude of orbital angular momentum depends upon orbital quantum number l and the orientation of angular momentum is determined by magnetic quantum number m.
Any change in these quantum numbers brought about in the hydrogen due to electromagnetic interaction leads to the hydrogen spectrum. The wavelength of emitted spectral lines, when electron transitions from one principal quantum number to other is given by Rydberg's formula, that is,
Where,
λ is the wavelength of the emitted photon.
R=1.0967×107 m-1 is the Rydberg's constant.
is the principal quantum number of the initial state.
is the principal quantum number of the final state.
This process of de-excitation of an electron is schematically represented below. It shows electron transitioning from some initial higher energy state to some final state and a photon is released in the process.
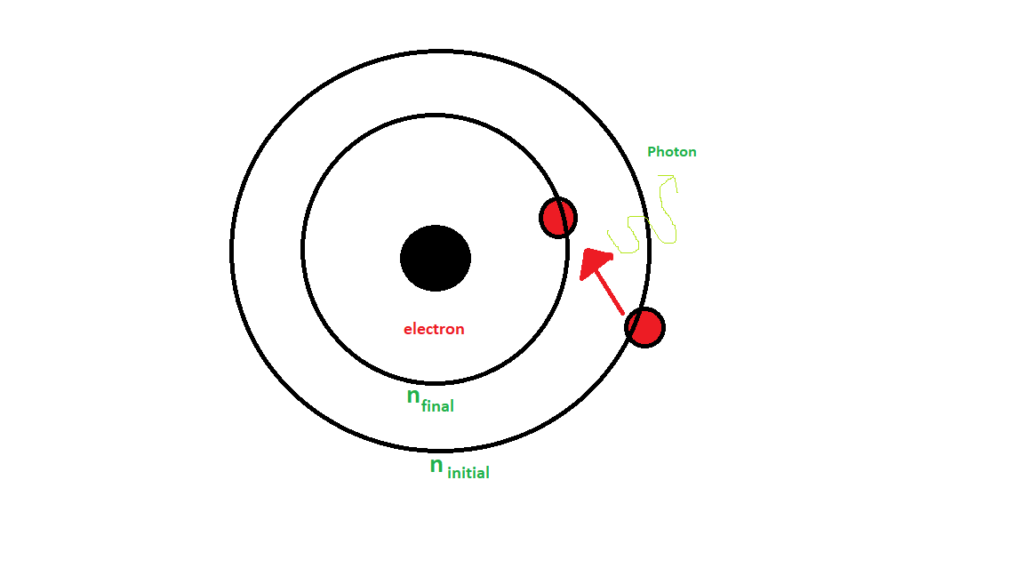
Depending upon the final state nfinal the electron falls in, the spectral lines can be categorized in series, as tabulated below,
| serial | transition | Series Name | Converging Wavelength |
| 1 | ∞ to 2 | Lyman series | 91.13 nm (Ultra Violet) |
| 2 | ∞ to 3 | Balmer series | 364.51 nm (Visible) |
| 3 | ∞ to 4 | Paschen series | 820.14 nm (Infa-Red) |
| 4 | ∞ to 5 | Brackett series | 1458.13 nm (Far Infra-Red) |
| 5 | ∞ to 6 | Pfund series | 2278.17 nm (Far Infra-Red) |
| 6 | ∞ to 8 | Humphreys series | 3280.56 nm (Far Infra-Red) |
Rydberg's formula is valid only for atoms that are atomically identical to the atomic hydrogen. Such an atom is also called a hydrogenic atom. It has only one electron under the influence of an effective nuclear charge +e. Such atoms include He+, Li2+, Be3+ and atoms where the electron is distant enough in such a way that all but one nuclear charge is effectively screened by other electrons. In such atoms, the outer electron feels a nuclear charge equivalent to +e.
Selection rules
Selection rules are the set of restrictions on the probability of transition of an electron from one state to another state. It specifies the allowed transitions that have a high probability of occurring or the transitions with very low or no probability of happening known as forbidden transitions. The allowed transitions are those in which the orbital quantum number of the electron changes by 1 and its magnetic number either remains constant or changes by one. Other transitions are rare.
Absorption spectra of sodium
The absorption of sodium is obtained when light from a continuous light source is made to pass through sodium vapor. The optically active electron in an atom absorbs quantized energy from the photons is the incident light, as it moves to a higher state under the selection rule, which states
where is the change in orbital quantum number, so when the pattern is observed on some screen, the wavelength corresponding to the absorbed photon is absent from it.
At room temperature nearly all atoms in vapor are in the ground state, the only possible absorption transition is where n>2.
When the electron in sodium absorbs a photon and goes from 3s to 3p then, the only possible transition is back to the 3s state. Whereas, if the absorbed photon promotes the electron to a 4s state then there are three possibilities for transition, as mentioned below.
Hyperfine structure
When the spectral line is examined under an instrument with a high resolution, it is pinpointed that the spectral lines further split into components with separation being of the order 1 cm-1. It is called hyperfine structure. It is due to nuclear structures such as the presence of different isotopic species in the sample under investigation. Since the energy level of isotopes is slightly displaced, relative to each other therefore it produces spectral transitions at slightly different wavenumbers. An interaction between the magnetic field due to the nucleus and the electron may shift the energy levels leading to a hyperfine structure.
Width of spectral lines
The spectral lines are not infinitely narrow. They do have a finite width as slits in the spectrometer. They have a width due to which a range of frequencies falls on the detector. The factors that contribute to the broadening of spectral lines are:
Collision broadening
Since atoms and molecules in the liquid or gaseous phase are always in motion, they keep colliding with each other. These collisions perturb the energies of the outermost energy state. It broadens the width of ultraviolet and visible spectra. This broadening is much more pronounced in liquid compared to gases.
Doppler broadening
The Doppler broadening of spectra lines is due to the doppler shift in the wavelength of light as the atoms emitting those radiations are always in motion.
Heisenberg uncertainty principle
Heisenberg's energy-time uncertainty relation
Smaller the uncertainty in the energy lesser the width of the spectral line. So, ground states are infinitely sharp as they are very long-lived states as compared to the excited states.
Common Mistakes
As discussed in the selection rule that the allowed transitions are those in which the orbital angular momentum changes by +1 or -1, all the transitions to the same orbital states are forbidden, whereas the spin quantum number m can either change by a unit or remains the same. However, there is no such restriction on the principal quantum number.
Related concepts
- Isometric shift
- Isotopic shift
- Plasma physics
- Spectral theory
- Thermionic emission
Practice Problems
Q1: Determine the wavelength of the photon emitted when an electron in a hydrogen atom undergoes a transition from n=5 to n=2.
- 456nm
- 865nm
- 750nm
- 434nm
Correct Answer : d) 434 nm
Explanation: Plugging the values in Rydberg's formula gives the correct answer.
Q2: What is the final state of an electron in the ground state of hydrogen atom absorbs a photon of wavelength 656nm.
- n=2
- n=3
- n=4
- n=5
Correct Answer : d) n=5
Explanation: Plugging the values in Rydberg's formula gives the correct answer.
Q3: What is the range of allowed orbital quantum numbers for principal quantum number n.
- I=0 to I=n
- I=1 to I=n
- I=0 to I=n-1
- I=n to I=n-1
Correct Answer : c) l=0 to l=n-1
Explanation: From selection rule we know that the angular momentum must change by unity for allowed transition.
Q4: Which of the following transition is forbidden?
- ∆l=1
- ∆l=-1
- ∆l=0
- ∆m=0
Correct Answer : c) ∆l=0
Explanation: From the selection rule, in allowed transition the angular momentum number changes by +1 or -1.
Q5: Identify the transitions from the list below which do not satisfy the selection rule.
Correct Answer : d.
Explanation: According to selection rules the transitions for which angular momentum remains constant are forbidden.
Context and Application
This topic is significant in the professional exams, especially for
- Bachelors of Science (Chemistry)
- Bachelors of Science (Astrophysics)
- Bachelors in Technology (Chemical Engineering)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Atomic Spectra Homework Questions from Fellow Students
Browse our recently answered Atomic Spectra homework questions.