What is the Balmer Series?
The spectrum of frequency observed when electromagnetic radiation is emitted from an atom when it goes from higher energy state to lower state, is known as emission spectrum. This transition occurs when an excited electron moves from higher to lower state. It has many possible electron transitions and each transition has a specific energy difference.
An emission spectrum is a series of various transitions that result in different radiated wavelengths. The emission spectrum of each element is distinct. As a result, spectroscopy will be used to distinguish elements in unknown matter. Likewise, molecule emission spectra could be used in chemical study of compounds. An emission spectrum is a series of various transitions that result in different radiated wavelengths. The emission spectrum of each element is distinct. As a result, spectroscopy will be used to distinguish elements in unknown matter. Likewise, molecule emission spectra could be used in chemical study of compounds.
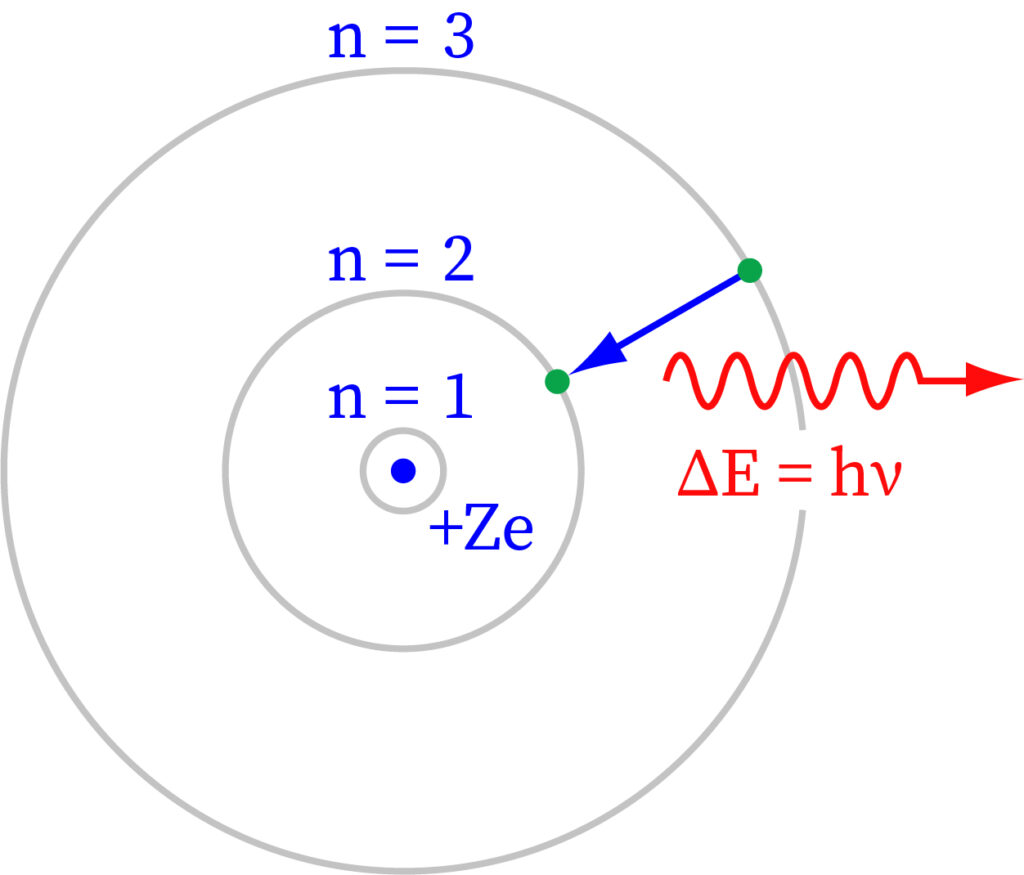
An electron orbits the nucleus of a hydrogen atom. The electromagnetic force between the electron and the nuclear proton causes the electron to enter a series of quantum states, each with its own charge. The Bohr model of the hydrogen atom depicted these states as separate orbits around the nucleus. As seen in the diagram, each energy state or orbit is denoted by an integer, n. The Bohr theory was successfully replaced by quantum mechanics, wherein the electron assumes an atomic orbital instead of an orbit, however the hydrogen atom's allowed energy levels persisted the same as in the earlier principle.
Concept
The spectral lines are organized into series based on ‘n’. Lines are numbered sequentially, beginning with the longest wavelength/lowest frequency of the series and progressing to the shortest wavelength/highest frequency of the series. The spectral series are very useful in the study of astronomical spectroscopy for detecting the presence of hydrogen and calculating red shifts.
We see series like Lyman series, Balmer series, Paschen series, Brackett series, Pfund series, Humphrey’s series. This comes from the Bohr model, when electrons shift from outer orbital to inner orbital.
The Balmer series contains transformation lines from an outer orbit n > 2 to an orbit n = 2.
Definition: Balmer series is nothing but series of spectral emission lines of hydrogen atom that are observed due to electron transition from higher levels down to the energy level with principal quantum number 2 (n =2).The Balmer formula empirically gives four transitions that are observable in the optical waveband. The Rydberg formula generalizes this and gives the other lines of hydrogen outside the optical field of the electromagnetic spectrum.
Here, is the wavelength, RH is the Rydberg constant for hydrogen and n1 and n2 are integers corresponding to principal quantum numbers involved in the transfer of electrons, here note that n2 > n1.
As hydrogen is readily available in the atmosphere and in universe, the Balmer lines are common feature in optical astronomy and it has various line corresponding to it, like for transition from 3 to 2 has wavelength of 6563 angstrom, and it gives pinkish or reddish color when images of ionized regions in planetary nebulae, supernova remnants and stellar nurseries.

Significance of Bohr Model
More specifically, the Balmer series correspond to transitions from the d, e, f,... energy levels (n3), where n is the principal quantum number) to the p energy levels (n=2). Just four of these spectral lines are visible; the others are in the ultraviolet range. Invisible ultraviolet photons accompany transitions to s energy levels (n=1). Invisible infrared photons accompany transitions to orbits d and beyond (n3). sharp spectral lines in the excited emission spectrum Hydrogen atoms imply that as time passes, the electron is in a configuration similar to one of the Bohr orbits, rather than a superposition of those states.
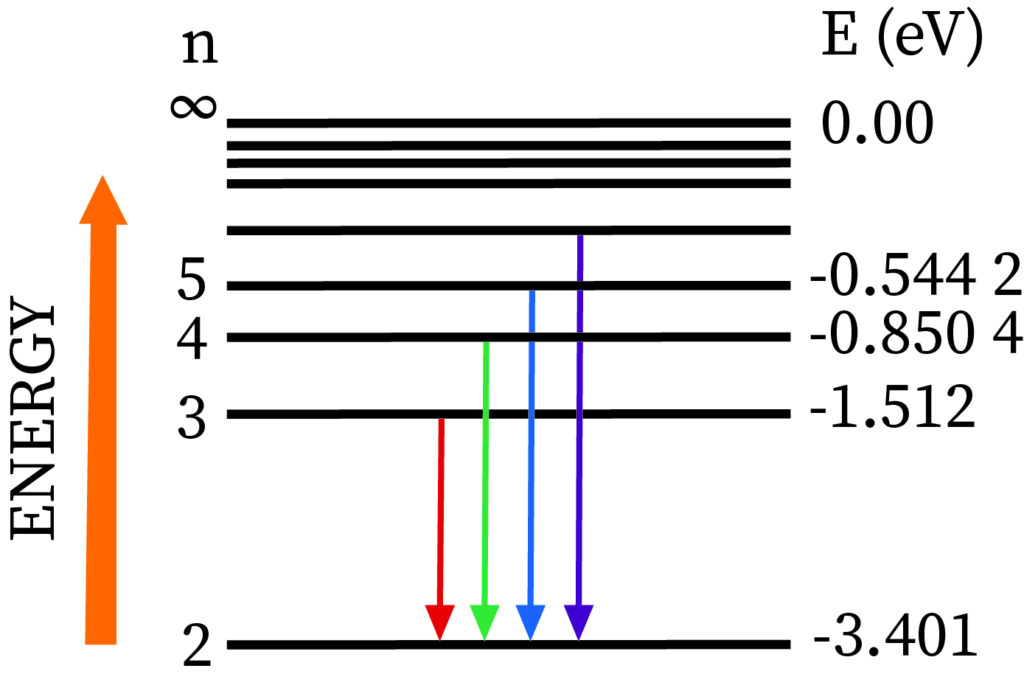
The quantum mechanical explanation is that electrons exist on Bohr orbits and leap from one orbit to the next. A more sophisticated interpretation is that detecting spectral lines leads to calculating energy, and hence the system ends up in an energy operator eigenstate (not in a superposition of such states). Mathematically, this theory makes no sense.
In particular, the lack of such superposition in long-time asymptotic conditions can still be understood in the form of a linear Schrödinger (or Dirac) equation with Coulomb potential, or any linear model for that matter. As a result, an accurate explanation of electron dynamics must account for nonlinear self-interaction of an electron with its own electromagnetic field.
The Schrödinger eigenstates are the extrapolations of such nonlinear eigenfunctions which need to be viewed as the system's attractor points in this dynamical context.
Application
The Bunsen-Kirchoff spectroscope is excellent for observing and measuring emission and absorption spectra. This spectroscope will be used to study the Balmer sequence of hydrogen and wavelengths of unknown gases in the current configuration. The spectrometer's scale tube is originally measured with a mercury light source so that the labelled numbers on the scale tube correspond to specific wavelengths of light. Following that, the absorption spectrums of hydrogen and nitrogen can be studied with the Balmer series.
The Balmer sequence is extremely effective in astronomy because the Balmer lines occur in a large number of stellar objects due to the excess of hydrogen in the universe, and hence are easily seen and comparatively solid opposed to lines from other elements.
Since the Balmer lines can be used in the spectra of several different objects, they are often used to calculate radial velocities due to doppler movement. This has many applications in astronomy, including the detection of binary stars, exoplanets, and compact objects such as neutron stars and black holes (by the motion of hydrogen in accretion discs around them), recognizing objects into groups with identical motions and probably sources (shifting groups, star clusters, galaxy clusters, and impact debris), defining distances (actually redshifts) of galaxies or quasars, and recognizing uncertainties related by spectrum analysis.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science in Physics
- Master of Science in Physics
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Balmer Series Homework Questions from Fellow Students
Browse our recently answered Balmer Series homework questions.