What do you mean by center of gravity?
The centre of gravity is a property that is based on the geometry of a rigid body or any particle. It is described as an equilibrium point or a hypothetical location where the total weight of the body is concentrated.
How to find the center of gravity of a system of particles?
Gravity is a natural force exerted by the earth on an object in the downward direction. In some situations, gravity causes the tumbling or overturning of unbalanced things. This can be better understood by considering the example of tightrope walkers who walk on their toes on a high rope. They wobble from one side to another but rarely fall down from the rope keeping their balance intact.
The center of gravity (COG) is an exact theoretical center about which the object would balance itself without undergoing any rotation. The motion of an object in space can be described as the translation of its center of gravity and the rotation (if allowed) about the COG.
At the COG, the total gravitational torque acting on the object is zero. The two necessary conditions for equilibrium or to locate the centre of gravity are:
- Summation of all the linear forces acting on a body should be zero.
- Sum of all the external rotary forces (torque) should be zero.
A symmetrical object composed of homogeneous material has a center of gravity that coincides with its geometric center. On the contrary, in an asymmetrical object consisting of heterogeneous parts of different masses, the center of gravity does not coincide with the geometric center.
Centre of gravity of an irregular shaped object
In order to find out the center of gravity of an irregular shaped body, such as a cardboard, we take a tipped object like a sharp pencil. By the trial method, mark a point on the surface of the cardboard where it attains balance on the tip of the pencil. This point is named as the centre of gravity of the cardboard.
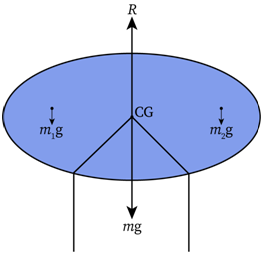
Suppose the total mass of the cardboard is m and the acceleration due to gravity is g. The total weight of the cardboard acting downwards will be mg. This force is counter balanced by the normal reaction R provided by surface in contact with the tip of the pencil in the upward direction. For translational equilibrium,
Hypothetically, assume that the cardboard is broken down into n particles of masses . The gravitational force acting on them will be , , ....
Thus, the mass of the ith particle is mi and the force of gravity is mig. If is the position vector of the ith particle from the centre of gravity of the cardboard, the torque acting about the COG will be given as,
... (1)
For equilibrium, the sum of external torques acting on all the particles should be zero. Thus,
... (2)
As the acceleration due to gravity g is a universal and a non-zero value, we can write equation (2) as:
... (3)
Equation (3) represents the condition where the COM of an object is located at the origin. The position vectors of all the particles of the cardboard are measured with reference to the center of gravity, i.e., from the origin. Hence, the center of gravity of the body coincides with its center of mass. In case of a solid sphere, both centre of gravity and centre of mass lie at its center.
Let the x and y co-ordinates of the ith particle be respectively.
From equation (3), solving for the x-coordinate of the COG, we get:
... (4)
Similarly, the y-coordinate of the COG will be:
... (5)
Relation between stability and center of gravity
The gravitational line of force is directed towards the earth’s center, such that it passes through the center of gravity. This line of gravity helps in understanding and determining an object’s ability to maintain balance. When the line of gravity falls from the base of the support, a reaction is required to maintain the balance of the body.
When the line of gravity is along the base of support, the object is said to be stable. When centre of gravity is less the body will be more stable. When centre of gravity is high then the object will topple over if it is pushed.
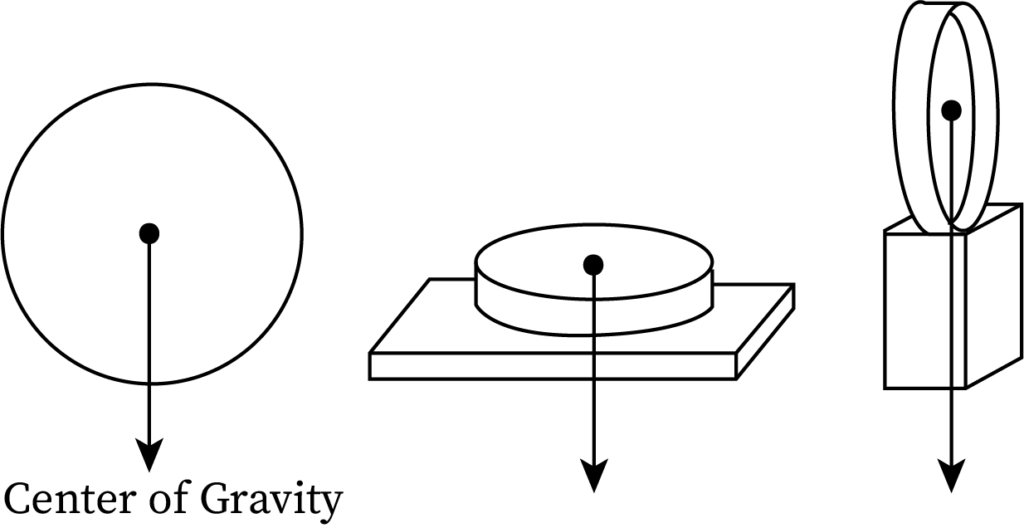
Center of gravity of a uniform ring and disc
The centre of gravity of a uniform circular ring lies on its exact center. It is directed outside the mass of the ring. When we place the ring on a supporting object the gravitational force acts through that object. This is the only way we can balance the ring.
In case of disk the centre of body and geometric centre will be same. Thus we did not need supporting objects to balance a disk of mass.
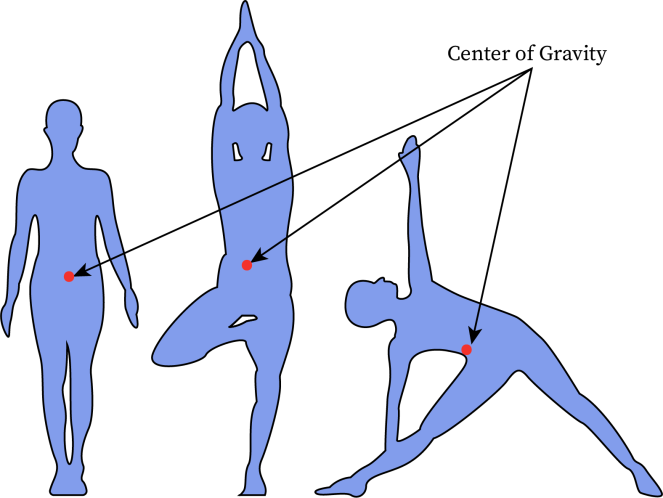
Where is the center of gravity of human body situated?
According to anatomical position, centre of gravity of human body lies just above the second sacral vertebra. But our body is not meant to remain fixed in the same anatomical position. The location of the centre of gravity changes whenever the position of human body shifts.
The overall position of our body parts will be different according to our actions, like running, standing, sitting etc. Also when we are carrying a weight, then that weight will affect the net weight of our body. Thus, the quantity of weight and the way we carry it also affect the location of our center of gravity. Thus the position of centre of gravity varies depending up on the position you take, the movement you make, what you carry and how you carry it.
Common Mistakes
Students often get confused between centre of mass and centre of gravity. Both these values coincide when there is uniform gravitational field. However, it will vary when gravitational field is not uniform.
The point at which distribution of mass is same in all directions is called the centre of mass of a body and it is independent of gravitational field. whereas the point at which the weight distribution of the body is equal in all directions is called the center of gravity.
Context and Application
This topic is significant for professional exams for undergraduate and postgraduate courses such as:
Bachelor of Science in Physics
Bachelor of Technology in Civil engineering
Bachelor of Technology in Mechanical engineering
Bachelor of Architecture
Master of Science in Physics
Related Concepts
Newton’s law of gravity
Law of conservation of mass
Law of mass action
Weight
Acceleration due to gravity
Practice problems
Q1: The method to calculate the centre of gravity of a body is:
(a) Taking the sum of moments of body divided by total weight of body.
(b) Taking the average mass of body divided by number of particles.
(c) Taking the area of body divided by average weight.
(d) Taking the volume of body divided by average mass.
Correct option: (a)
Q2: What is the position of center of gravity in a human body according to its anatomy?
(a) At the centre of diaphragm
(b) Anterior to second sacral vertebra
(c) Near the thyroid gland
(d) Above external oblique
Correct option: (b)
Q3: The two necessary conditions for the equilibrium position of any object/body are:
(a) Summation of all the linear forces should be constant and of all torques acting on a body should be zero.
(b) Summation of all the external linear forces acting on a body should be zero and of all torques should be non-zero.
(c) Summation of all the linear forces and of all torques acting on a body should be greater than zero.
(d) Summation of all the linear forces and of all torques acting on a body should be zero.
Correct option: (d)
Q4. Where is the centre of mass of an equilateral triangle locates?
(a) At the point of intersection of medians.
(b) At point having distance equal to half of height from the base.
(c) At a distance double that of height of length side.
(d) At the midpoint of line connecting midpoints of adjacent sides.
Correct option: (a)
Q5. Which of the following statement is wrong regarding centre of mass and centre of gravity?
(a) The center of mass of a body is a theoretical point at which the mass distribution is equal in all directions.
(b) The center of mass and center of gravity are at the same position when the gravitational field is uniform.
(c) The center of gravity is a point at which the weight distribution is equal in all directions.
(d) Both centre of mass and centre of gravity depends on the gravitational force.
Correct option: (d)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Center of Gravity of a system Homework Questions from Fellow Students
Browse our recently answered Center of Gravity of a system homework questions.