What do we mean by Circular Motion?
We can simply define a circular motion as a motion that is carried out by a body that happens along a path that is shaped like a circle. We generally have two types of circular motions. They are uniform and non-uniform circular motion. We determine whether a particle is moving in a circular motion or not by checking its movement. If it moves in a path which is along the circumference of a circle, then the particle is undergoing circular motion. Else, it is not.
Concept of Circular Motion
We observe a lot of objects in our daily life in which some of them are in a moving state; some of them are in resting state. We can say a particular body is at rest when it shows no positional change as compared to its surroundings. For instance, a bottle kept on a table, or a bench fixed under a tree are bodies at rest. On the contrary, when an object shows significant positional change as compared to its surroundings with respect to time, then the body can be defined as a body in motion. For instance, a moving train, a rotating fan, a man walking, and so on.
There are different types of motion such as translation motion, rotatory motion, oscillatory motion, and so on. In this article, we will discuss circular motion only.
As stated before, if a body moves in such a manner that its movement goes along a path shaped like a circle, then the undergone motion can be termed as circular motion. This type of motion can be treated as a case that falls under the category of curvilinear motion. In such a motion, the distance between the center and the object which is moving will remain constant. We see simple examples of circular motion in our everyday life. For example, the movement of a ceiling fan, movement of the planets, the rotation of a wheel, and so on are all examples of circular motion. The distance between the center and these moving objects always remains the same, irrespective of their position with respect to time.
What is Acceleration?
Acceleration is the phase where an object’s velocity transforms rapidly at a single point. Usually, when there is a change in the direction in which the motion takes place, or there is a change in the magnitude of the force, in both cases, the velocity can change.
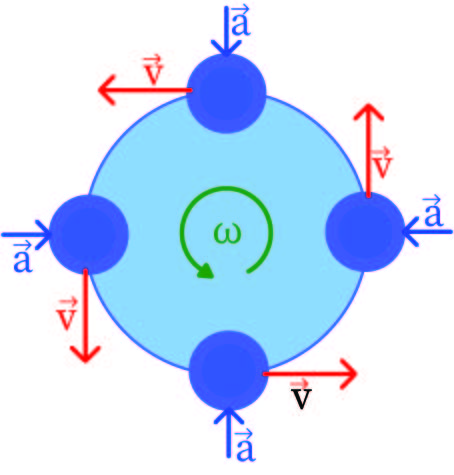
In a circular motion, a major contrast that exists with linear motion is that the direction in which the motion is taking place is constantly changing in the case of circular motion. As a result, angular variables are used for describing circular motion.
What are Angular Velocity and Angular Displacement?
We can define the term angular displacement as the change in angle that is carried out by an object in rotation per unit time. In a circular motion of a particle, the angular displacement’s changing rate can be defined as angular velocity.
Similarly, for a rotating object, the angular velocity’s changing rate can be described as the angular acceleration. Usually, we can find two different components when a particle undergoing circular motion is accelerated. These are radial and tangential acceleration. Tangential acceleration acts in the same direction as the velocity of the said particle.
The radial component acts in the direction that goes toward the circle’s center. In a circular motion, the direction in which the particle’s velocity moves is changed by the radial acceleration. The velocity’s direction is changed at every point in a circular motion. Thus, we can say that there is a non-zero value for the radial component. On the other hand, depending on the type of circular motion, the value of the tangential component can change. It will be zero when the circular motion is uniform, and it will be either negative or positive when the circular motion is non-uniform.

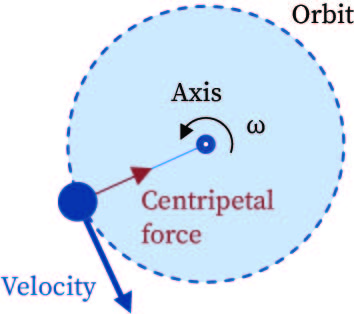
What is Centripetal Force?
In a circular path, the center always experiences a force directed towards it. This is known as the centripetal force. It can be expressed as-
Here, the particle’s mass is denoted by ‘m’. The term ‘v’ stands for the velocity of the particle, and ‘r’ stands for the circle’s radius in which the particle is undergoing a circular motion.
What is Uniform Circular Motion?
An object can be said to be in a phase of acceleration when there is a change in the velocity of the object. Usually, with the change in the magnitude, or with a change in the direction in which the motion takes place, the velocity of an object can be changed.
Consider a body moving in a rectangular closed path. Assume that a man walks at uniform speed on the straight parts of the rectangle. To keep on track, speed has to be quickly changed at the corners of the rectangle. In the above case, to move in a rectangular track, the direction of motion has changed four times.
Suppose we are taking a hexagonal track instead of the rectangular path. When the object is moved down the hexagonal path, the direction will be changed 6 times in one complete rotation.
It is observed that as the number of sides increases, the more we have to take turns. A circle has an infinite number of sides. Thus, the direction is changed at each point. If an object is moved in a circle while keeping a constant magnitude in velocity, then the only reason why the velocity is changing is that the direction of motion is changing at every point in the circle. Hence, an object going in a path of a circular shape will still undergo acceleration.
If we consider a circle that has a radius equal to ‘r’, then we denote the circumference by 2πr. If we denote the speed by ‘v’, and the time taken to cover the circumference is given by time = t, then we denote the speed as-
We define uniform circular motion as the motion undergone by an object moving with a uniform speed along a path of circular shape.
To show that the direction of motion changes in a circular motion, we can conduct the following experiments. If we rotate a stone tied with a thread on its end, we will see a circular motion of the stone. If we let the thread go at any moment, we will see that the stone will fly away in a direction that is tangent to the circular path, and it is a straight line. This proves that in a circular path, the direction of motion changes at every point.
As for other real-life examples, we find athletes competing in discus throw or hammer throw use the same method. They move in a circular motion and let go of the object at the desired point, such that it can fly away in a straight line to cover as much distance as possible.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate
- Bachelors in Science (Physics)
- Masters in Science (Physics)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Circular Motion Homework Questions from Fellow Students
Browse our recently answered Circular Motion homework questions.