What do you Mean by Collision?
Collision, also known as impact in physics, is the unexpected, forceful coming together of two bodies in direct contact. Two objects collide as they come into close contact with each other. During collision the bodies exert momentary forces on each other. For example, two billiard balls, a golf club and a ball, a hammer and a nail head, or a falling object and a floor. The properties of the materials with which the objects are made, the force of collision as well as the time duration of contact influence the outcome. If a hard steel ball is made to drop on a steel plate, it bounces to nearly the same initial level, while a lead ball, if made to fall will not bounce back. The effect of a steel ball on a plate is said to be elastic, while the effect of putty or lead balls on a plate is said to be inelastic.
There are three types of collisions, namely:
Elastic Collision
An elastic collision is one in which the system suffers no net kinetic energy loss as a result of the collision.
Real-Life Examples of Elastic Collision
- When a ball at a billiard table hits another ball, it is an example of elastic collision.
- When you throw a ball on the ground, and it bounces back to your hand, there is no net change in the kinetic energy, and hence, it is an elastic collision.
Inelastic Collision
An inelastic collision is a type of collision where there is a loss of kinetic energy but momentum is conserved. Thermal energy, sound energy, and material deformation are all results of the lost kinetic energy.
Real-Life Examples of Inelastic Collision
- The ball is dropped from a certain height, and it is unable to rise to its original height.
- When a soft mudball is thrown against the wall, it will stick to the wall.
Perfectly Inelastic Collision
This is a special case of inelastic collision. Here, the outcome after collision is that the two objects stick together.
Collision of One Dimensional (1D) bodies
One sudden dimensional interaction of masses is that collision in which both the initial and final velocities of the masses lie in one line. In a single dimension, all motion variables are found.
Elastic One-Dimensional Collision
Internal kinetic energy and momentum are also conserved, as we saw in the elastic collisions. Elastic collisions can only be accomplished with microscopic particles such as electrons, protons, and neutrons.
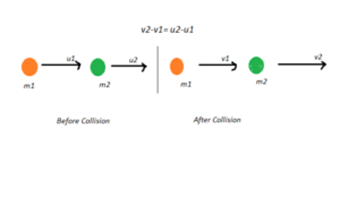
By kinetic energy conservation, we have:
Using the conservation of momentum equation:
Now dividing the two equations:
We get:
Now,
When we use this value of v1 in equation of conservation momentum we get
Now using the value of v2 in equation v1 = v2 + u2– u1
We finally get:
When masses of both the bodies are equal, then generally after the collision, these masses exchange their velocities.
and
This means that in the course of a collision between objects of the same masses, if the second mass is at rest and the first mass collides with it, then after the collision, the first mass comes to rest and the second mass moves with speed equal to first mass. Therefore, in such a case, and.
In case if then, and
This means that the lighter body will bombard back with its own velocity, while the heavier mass will remain static. However, if m1 > m2, then v1 = u1 and v2 = 2u1
Inelastic Collisions
The objects in an inelastic collision stick to each other or travel in the same direction. The total kinetic energy in this form of collision is not conserved, but the total momentum is conserved. The energy is converted into other energy sources such as heat and light during this type of collision. Since the two masses obey the law of conservation of momentum and travel in the same direction at the same speed v during the phenomenon, we have
Where,
- V= Final velocity
- M1= Mass of the first object in kgs
- M2= mas of the second object in kgs
- V1= initial velocity of the first object in m/s
- V2= initial velocity of the second object in m/s
Inelastic One-Dimensional Collision
In inelastic one-dimensional collision, the colliding masses stick together and move in the same direction at the same speeds. Law of conservation of momentum:
Final velocity is same for both, so taken as v (as they stick together). Now v shall be:
The kinetic energy lost during the phenomenon shall be:
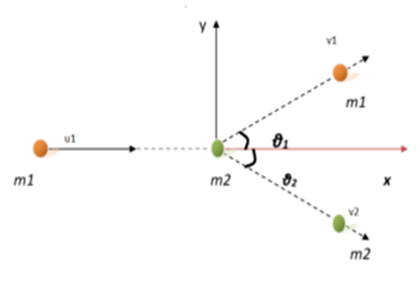
Collision of Two Dimensional (2D) Bodies
The collision involves two masses m1 and m2. The v1 is the speed of particle m1. The particle with mass m2 is at rest. The stationary object of mass m2 collides with the object of mass m1 in this situation. The masses m1 and m2 move in opposite directions as a consequence of the interaction.
Billiards is a game played on a felt-covered table with a cue stick and several balls. A game called pool is one of the most common variations of billiards. In a pool, players use the cue stick to strike a white ball called the cue ball to hit other similar balls into semi-circular holes called pockets along the inner edge of the table. The pool involves 15 coloured balls, a cue ball, and a pocketed table.
The velocity of the balls will change when they collide with each other or the table walls. A change in velocity may occur as a result of a change in speed, direction, or both. If the ball’s velocity changes, so do its momentum. Impulse is the term for this change in momentum over time.
The stick is moving towards the ball at high speed. After the collision, the stick stops moving. It transfers some of its kinetic energy to the forward-rolling cue ball. However, friction between the ball and the table loses some of the kinetic energy, allowing the ball to roll.

- Collisions can be used as an experimental technique to study the material properties of objects and other physical phenomena.
- Collision in two dimensions follows all the rules of collision in one dimension.
- The momentum of the system is conserved in elastic and inelastic collision in two dimensions.
- The kinetic energy of the interacting particles is conserved inelastic collision.
- Real-life collision may take place in two or three dimensions.
- The velocity of interacting particles can be found by considering the collision in each of the dimensions by selecting suitable components of the velocity vector.
Elastic Collisions

In the elastic collision, total momentum, total energy and total kinetic energy are conserved. Even then, the overall mechanical energy is not transformed into any other energy source as the forces concerned in the short interaction are conserved in nature. The above figure shows two balls, out of which one was at rest, colliding. After collision, they move in different X and Y directions. The components of the velocity is resolved and law of momentum conservation is written as
Where,
- m1 = Mass of 1st body
- m2 = Mass of 2nd body
- u1 =Initial velocity of 1st body
- u2 = Initial velocity of the second body
- v1 = Final velocity of the first body
- v2 = Final velocity of the second body
Common Mistakes
- People sometimes think that objects must stick together in an inelastic collision. People sometimes think that objects must stick together in an inelastic collision but they do so only in perfect inelastic. Objects may also bounce off each other or explode apart, and the collision is still considered inelastic as long as kinetic energy is not conserved.
- Sometimes people think kinetic energy is only lost during inelastic collisions. Collisions are considered inelastic when kinetic energy is not conserved, but this could be from either a loss or gain of kinetic energy. For example, in an explosion-type collision, the kinetic energy increases.
Context & Applications
- Engineering Students.
- Bachelors in Science (Physics)
- Masters in Science (Physics)
Related Concepts
- Momentum& Kinetic Energy
- Coefficient of restitution
- Force
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Collision Theory Homework Questions from Fellow Students
Browse our recently answered Collision Theory homework questions.