What is a combination of capacitors?
Capacitors are electric devices that store energy. They store this energy as an electric charge. Capacitors are devices that oppose changing voltage. S.I. unit of capacitance is Farad (F). One Farad is described as one coulomb per volt. The capacitor consists of two electrical conductors, called plates, which are some distance apart from each other. Space between these capacitor plates can be either vacuum or be filled with an insulating material called a dielectric. A dielectric is a bad conductor of heat and electricity which has no free electrons, which could lead to current path formation or device heating up. Practically, no current can pass through a dielectric. Examples of dielectric materials are glass, paper, transformer oil, etc.
Factors that determine the capacitance
Some factors largely determine the capacitance. These factors are -
- The surface area of capacitor plates - Greater will be the surface area, more will be the value of capacitance.
- The types of dielectric used between the plates - dielectrics are bad conductors of heat and electricity.
- Distance between the capacitor plates
Capacitors are widely used as energy storage devices and also for power factor correction. They are used where we only want alternating current to pass and block the direct current. Capacitors are connected in many of our daily use devices and equipment. They are present in our smartphones, electric vehicles, electric ceiling fans. Capacitors help to start a fan and also help it move. A very important point that we need to keep in mind regarding the capacitors is that capacitors allow current to pass only when it is charging or discharging.
In an electric circuit, more than one capacitor can also be installed depending upon the requirement. When one capacitor is connected to the circuit, calculations are easy. But when more than one capacitor is connected, first of all, we need to find the equivalent capacitance or total capacitance, and then only we can proceed further with our calculations. For any capacitor, capacitance is related to the charge and voltage.
When the second plate of the first capacitor is connected to the first plate of the second capacitor, those two capacitors are said to be connected in a series arrangement. In this type of connection, the voltage developed across each capacitor is different but the charge distribution is the same. More than two capacitors can also be arranged in this manner. When these capacitors are connected to a battery source, they exhibit identical charges.
Many capacitors connected in series are solved such that they are equivalent to one capacitor whose capacitance is always smaller than the smallest capacitor in the series network. The charge developed on the equivalent capacitor will be the same as the charge on each capacitor in the series arrangement. Connecting capacitors in a series are similar to increasing the distance between the capacitor plates. They both have the same effect.
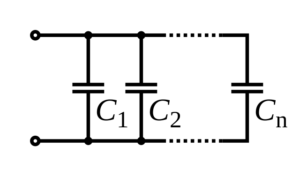
There is a second case when the capacitors are in parallel combination. In that case, the total capacitance is the sum of the individual capacitance of the capacitors connected in parallel. Connecting capacitors in parallel combination are similar to increasing the area of capacitor plates. They both have the same effect.
Connection of capacitors
The connection of capacitors can be established in a circuit in two ways.
- Series
- Parallel
- Combination of series and parallel
In a series connection, capacitors are connected such that the total charge distribution across each capacitor will be equal whereas the voltage drop across each capacitor will be different.
In a parallel connection, individual capacitors are connected such that the voltage drop across each capacitor is equal whereas the total charge distribution across each capacitor is different.
In the combination circuit wherein capacitors are connected in series as well as parallel combination, firstly we need to identify which all capacitors are in series and which ones are in parallel and then compute their equivalent capacitance. We find the equivalent capacitance for series and parallel connected capacitors separately and then solve further such that only one capacitor remains in the circuit whose value is equivalent to all the capacitors connected in that very circuit.
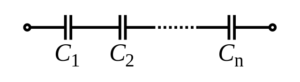
Solving for equivalent capacitance
When more than one capacitor is connected in an electric circuit, equivalent capacitance or total capacitance is calculated. Equivalent or total capacitance means the overall value of all the capacitors connected in series combination or parallel combination. All the capacitors in a circuit can be replaced with just one equivalent capacitor for further calculations and circuit simplification.
For equivalent capacitance in case of a series combination
...................(1)
where n is the total number of capacitors connected in series.
For equivalent capacitance in case of a parallel combination
...................(2)
where n is the total number of capacitors connected.
In the case of the parallel combination of capacitors, individual capacitance is added together to get total capacitance or equivalent capacitance. Here, the voltage across each capacitor is equal but the charge distribution across each capacitor is different.
When one capacitor is present in an electrical circuit, individual capacitance is taken into account. When more than one capacitor is present, we take total capacitance or equivalent capacitance into account.
Solving a combination of capacitors
When one capacitor is present in an electric circuit, it is easy to solve the circuit. We can solve for charge or voltage using the formula Q=CV where Q is the charge, C is the capacitance and V is the voltage.
But when more than one capacitor is present in a circuit, the first step towards solving that circuit is to find the overall capacitance or equivalent capacitance and then solve for Q or V or I.
Equivalent capacitance can be computed using the formula given above. Let us understand how to solve the combination of capacitors with the help of an example.
Uses of capacitors
There are several applications of a combination of capacitors. Mostly, the combination of capacitors is done where multiple capacitors are connected and we need to do the circuit study to find voltage or current or charge.
It is very helpful to find the values quickly and more accurately. When we want to compute the energy stored by the capacitors, we need to find the equivalent capacitance.
To simplify a bulky circuit wherein multiple capacitors are connected in series as well as in parallel, this method comes in really handy where we simplify the circuit and calculations then become so much easier.
Practice Problems
Q1: If five different capacitors are connected in parallel combination, what will be their voltage drop?
- Same
- different
- no relation to capacitors
- inversely proportional to the capacitance
Answer: (a) If four different capacitors are connected in parallel, the voltage drop across each capacitor will be the same.
Q2: If three capacitors are connected in series combination, what will be their charge?
- different
- same
- no relation to capacitance
- infinite charge accumulation
Answer: (b) If three different capacitors are connected in a series combination, the charge accumulated on each capacitor will be equal. All the capacitors will have equal charge distribution.
Q3: If two capacitors of capacitance 5 F and 2 F are connected in parallel combination, what will be the equivalent capacitance?
- 107 F
- 7 F
- 10 F
- 5 F
Answer: (b) The formula for equivalent capacitance in case of a parallel combination of two capacitors, let us say C1 and C2, will be:
Hence our correct answer will be 7 F.
Q4: Two capacitors with capacitance values 2 F and 6 F are connected in a series arrangement. What will be the equivalent capacitance?
- 1.5 F
- 2.3 F
- 3.2 F
- 6 F
Answer: (c) When two capacitors, say C1 and C2 are connected in a series arrangement, the formula for equivalent capacitance will be , hence
Q5: How does the effective capacitance of two or more identical capacitors behave in a series combination?
- remains same
- increases
- decreases
- can't say anything
Answer: (c) In series combination of identical capacitors, the effective capacitance decreases. This can be seen by the formula . Hence the correct option is (c).
Formulae
- The equivalent capacitance in a series connection is given by,
The equivalent capacitance in the case of a parallel connection is given by
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Combination of Capacitors Homework Questions from Fellow Students
Browse our recently answered Combination of Capacitors homework questions.