What is the de Broglie Equation?
The de Broglie equation was given by French scientist L. de Broglie in 1924. This equation describes the wave-particle duality. It also describes the type of electron wave. The de Broglie equation relates the symmetry between electromagnetic radiation and microscopic particles like electrons. According to the de-Broglie hypothesis, all moving particles, whether microscopic or macroscopic, will show a wave nature. The waves associated with the moving particle are called matter waves. The mathematical expression for the de-Broglie equation is
What is the Derivation of the de Broglie Equation?
According to De Broglie, the wavelength of the matter wave associated with the particle is:
...(1)
Here,
h = Planck’s constant
λ = wavelength of the matter wave associated with the particle
The momentum of the particle is given by
...(2)
On substituting (2) in (1), the wavelength of the matter wave associated with the particle is:
...(3)
Graph Between the de Broglie Wavelength and Velocity
From equation (4), the de Broglie wavelength (denoted by λ) is inversely proportional to its velocity. The nature of the graph drawn between them is hyperbolic as shown below:
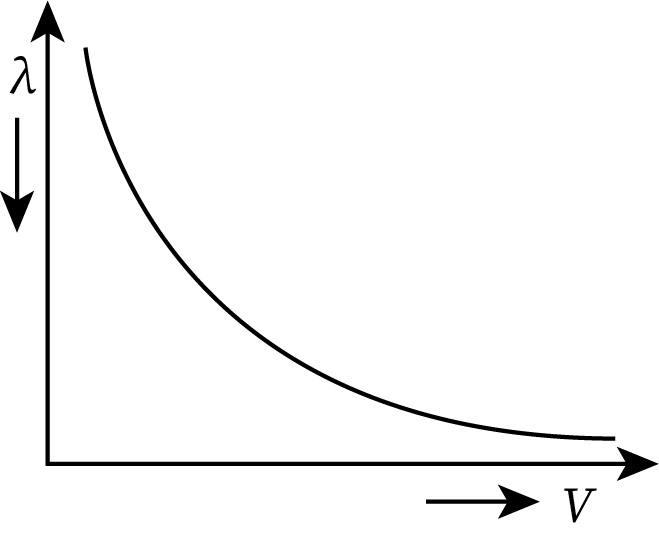
- For the lighter particles, the de-Broglie wavelength is larger as compared to the heavier particles.
- If the velocity of a particle increases, then its de-Broglie wavelength decreases.
- The de-Broglie wavelength has no dependence on the nature of the particle.
Why is the de-Broglie Wavelength Applicable Only to Microscopic Particles?
Microscopic particles like electron, proton, hydrogen atom, etc. have very small masses as compared to the macroscopic particles which are quite heavy.
The de-Broglie wavelength is inversely proportional to the mass of a particle. Therefore, for heavy particles, the wavelength becomes too small such that it is not easy to measure.
Consider a comparison between an electron and a ball of mass 2 kg, both moving with a velocity of .
From equation (4), we get:
The de-Broglie wavelength for the electron is:
The de-Broglie wavelength of the ball is:
From the above calculations, it is clear that for macroscopic particles, the de-Broglie wavelength is very small to be measured. That is why this equation is applicable to only microscopic particles.
Relation between the de-Broglie Wavelength and Kinetic Energy
The expression for the kinetic energy of a moving body is:
...(4)
Multiplying mass m on both sides of equation (4), we get:
The momentum of the particle is:
...(5)
From equations (4) and (5), the de-Broglie wavelength is:
...(6)
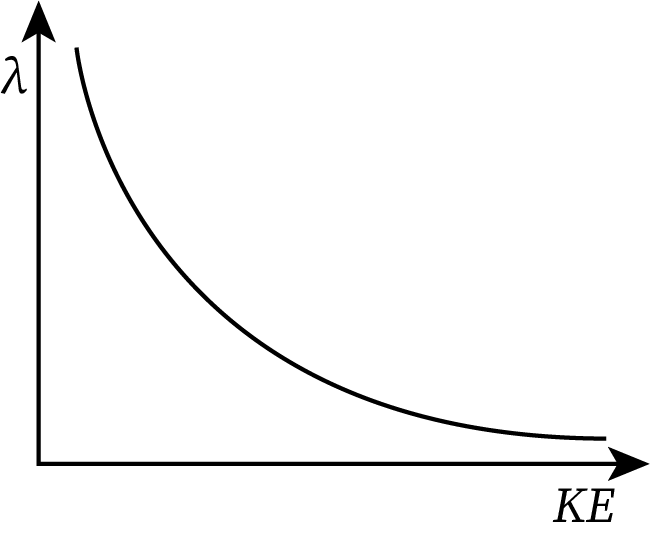
Graph Between the de-Broglie Wavelength and Kinetic Energy
From equation (6), the de-Broglie wavelength (denoted by lambda) is inversely proportional to the square root of the kinetic energy of the moving particle.
Relationship between the de-Broglie Wavelength and Potential Difference of an Accelerated Electron
The kinetic energy of a particle-like electron is equal to the energy acquired from accelerating through potential difference.
...(7)
Here,
V = potential difference applied
e = charge on electron
From equations (6) and (7):
...(8)
Calculation of the de-Broglie Wavelength for an Electron
The mass of an electron,
The charge on electron,
The value of Planck’s constant,
Substituting the values in equation (9), we get:
The wavelength of an electron is:
...(8)
Derivation of Bohr's Theory from the de-Broglie Equation
According to Neil Bohr’s postulate, the angular momentum of electron in an electron in the orbit is quantized and is an integral multiple of .
Consider an electron revolving in its orbit of radius r. The wave function associated with the electron forms a series of crests and troughs.
The wavelength of the electron wave is equal to the circumference of Bohr's orbit.
...(11)
Here, n =number of waves
The wavelength is:
...(12)
From equations (12) and (7):
...(13)
On solving equation (13), we get:
...(14)
Here, v = velocity of electron
From equation (14), the angular momentum of electron =
Therefore, the de-Broglie theory explains Bohr's quantization of angular momentum.
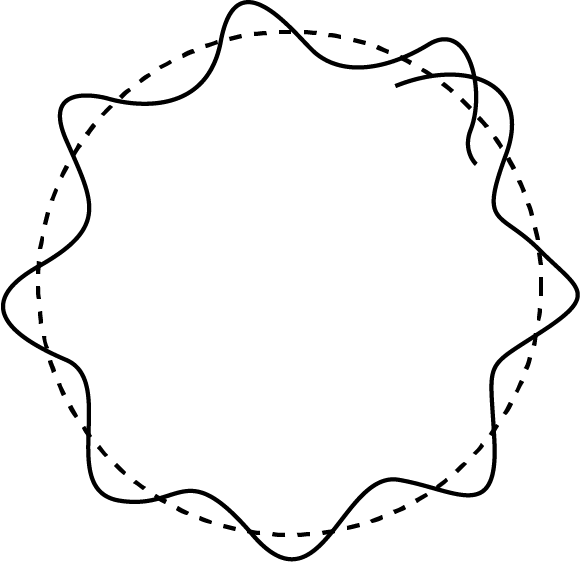
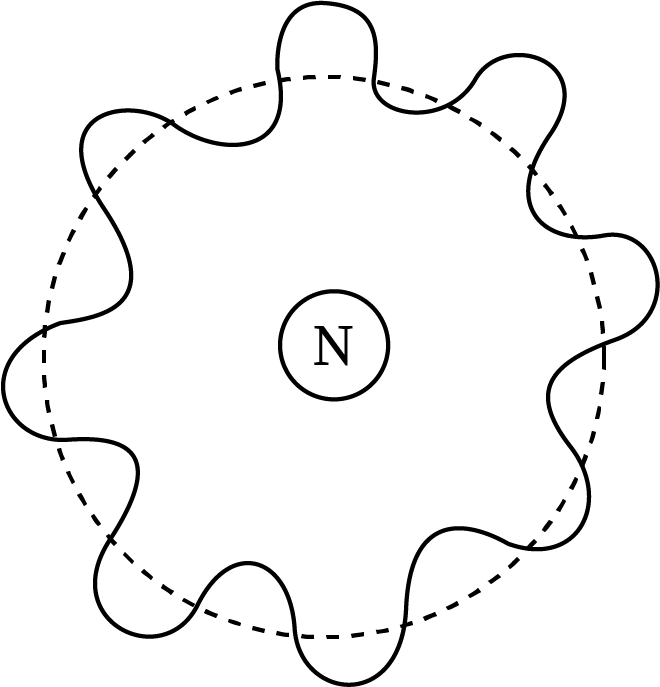
Sketch Showing the de-Broglie Wavelength Associated with Bohr's Model
The electron waves form crest and troughs on the Bohr's atom, which contains both waves in phase and waves out of phase.
How is the Davisson-Germer Experiment Related to the de-Broglie Equation?
In 1927, Davisson-Germer proved the similarity in the diffraction pattern between electrons and X-rays. They calculated the wavelength of matter waves due to diffracted electrons as 0.165 nm.
From equation (13), the wavelength of the electron at 54 V is:
Therefore, Davisson-Germer confirmed the de-Broglie hypothesis and wave nature of electrons.
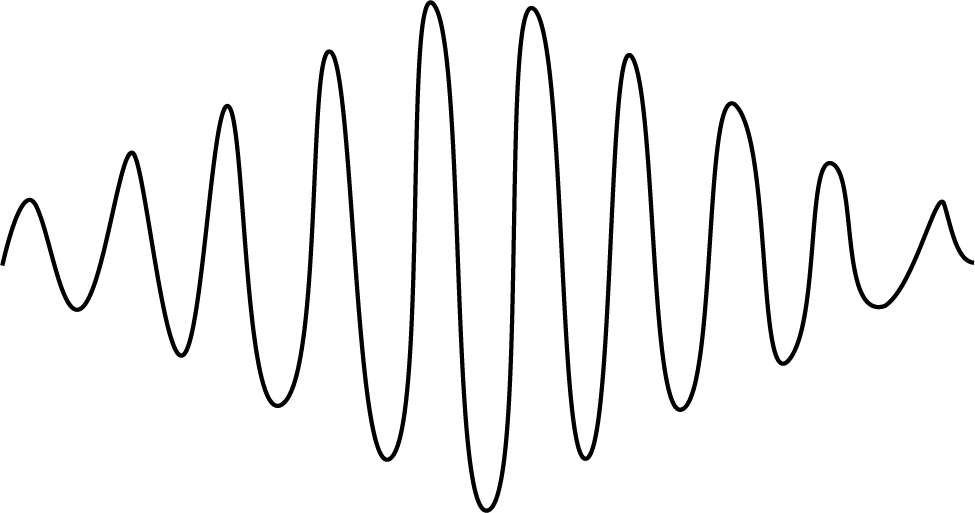
Pictorial Difference Between Matter Waves and Electromagnetic Waves
The sketch of EM waves containing a perpendicular electric field and a magnetic field is drawn below:
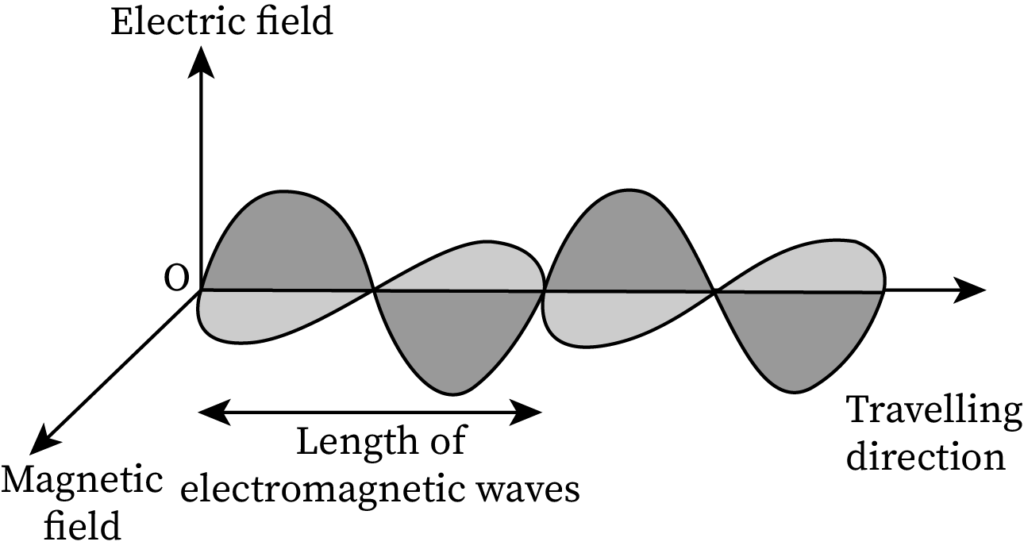
The sketch of matter waves is drawn below:
Common Mistakes
Students often get confused with electromagnetic waves (EM Waves) and de Broglie matter waves. They interpret the nature of both the waves to be the same, which is incorrect.
Electromagnetic waves differ from matter waves in the following ways:
- EM waves contain both an electric field and a magnetic field, whereas de-Broglie matter waves do not contain any field.
- EM waves can even propagate in vacuum, whereas matter waves find it hard to propagate in vacuum.
- EM waves are created through accelerated charged particles, whereas matter waves are associated with moving particles.
- EM waves propagate with the velocity of light in vacuum while the speed of matter waves is less than the velocity of light in vacuum.
- EM waves include radio waves and ultraviolet light while matter waves include the electron beam.
- The formula for electromagnetic wavelength is λ=cv and that of the de-Broglie wavelength is
- The energy of EM waves is quantized but the energy of matter waves is not quantized.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
Bachelor of Engineering in Mechanical Engineering
Bachelor of Engineering in Chemical Engineering
Bachelor of Science in Physics
Master of Science in Chemistry
Quantum Mechanics
Related Concepts
Photoelectric Effect
Bohr's Quantization of Angular Momentum
Schrodinger's Wave Equation
Quantum Mechanics
Planck's Quantum Theory
Heisenberg's Uncertainty Principle
Practice Problems
Q.1 Which of the following represents the de-Broglie equation?
(a)
(b)
(c)
(d)
Correct option: (a)
Q.2 Which of the following indicates the use of the de-Broglie equation?
(a) The de-Broglie equation is used for determining the number of spectrums associated with any particle.
(b) The de-Broglie equation is used for the calculation of the wavelength associated with any microscopic particle in motion.
(c) The de-Broglie equation is used for measuring an emission from the surface.
(d) There is no such use of the de-Broglie equation in real life.
Correct option: (b)
Q.3 Which of the following is the correct reason for the de-Broglie equation to be applicable to only microscopic objects?
(a) In the case of macroscopic objects, the de-Broglie wavelength is very small; hence, it is difficult to measure. That's why the de-Broglie equation is applicable to only microscopic objects.
(b) Microscopic objects do not show wave-particle duality.
(c) For microscopic objects, it is easy to identify the emission rate.
(d) In the case of microscopic objects, the spectrum is clear in comparison to macroscopic objects.
Correct option: (a)
Q.4 Which of the following represents the correct de-Broglie hypothesis?
(a) According to the de-Broglie hypothesis, all macroscopic particles show wave-particle duality.
(b) According to the de-Broglie hypothesis, all microscopic particles in motion show wave-particle duality.
(c) According to the de-Broglie hypothesis, no particle shows the wave-particle duality.
(d) According to the de-Broglie hypothesis, the emission of the spectrum from microscopic particles has a wave nature.
Correct option: (b)
Q.5 Which of the following represents the ratio of the kinetic energy of electrons if the de-Broglie wavelength of the electron waves in two orbits is 3:5?
(a) 25:9
(b) 125:27
(c) 5:3
(d) 10:6
Correct option: (a)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
de Broglie Equation Homework Questions from Fellow Students
Browse our recently answered de Broglie Equation homework questions.