What is Debye model theory?
In solid-state physics, debye theory is used to estimate the phonons contributing to the specific heat capacity in a solid. It explains that the specific heat is a consequence of the vibrations of the atomic lattice of the solid, which is in contrast to the Einstein model. In the Einstein model, solids are treated as independent, non-interacting quantum harmonic oscillators. This model clearly explains the low-temperature dependence of the heat capacity, which is proportional to T3. This is known as Debye T3 law.
Introduction to Debye’s theory
In 1912, Peter Debye found the debye model of specific heat capacity. The Einstein model of specific heat of solid consider each atom as an individual atom and gave only the correct high temperatures limit. But debye model explains that there are a maximum number of modes of vibrations in solid and framed the vibrations as standing wave modes.
This model is similar to black body radiation, where electromagnetic radiation acts as a photon gas. The density of states of modes is called phonons–quanta of sound waves.
Debye found that the harmonic oscillation of atoms is the same as sound. As sound is also a wave, it should be quantized the same way as Planck quantized light. There is only one difference between the light and sound wave: for light, there are two polarizations for each wave vector k, whereas sound has three modes for each wave vector. One in longitudinal mode, atomic motion is in the same direction as, k, and the other two are transverse mode, where the wave motion is perpendicular to the wave vector k. Light has only transverse mode.
Derivation of Debye's specific heat capacity
To determine the low-temperatures capacity of the heat, it is important to go beyond the assumption of the Einstein model which states that all the modes have the same frequency. As an alternate, we have to find and count the number of modes present in the crystal structure based on its model. In the crystal, the modes are standing waves.
The number of possible wave numbers (k) for a significant crystallographic orientation is,
Here, L is the size of the grain and N is the number of atoms along with the orientation of the crystal, respectively.
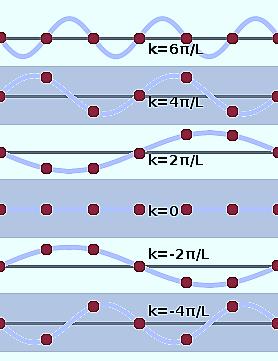
Oscillation with wave vectors falls outside the brillouin zone boundary. By counting the different wave numbers, we understand that for one dimension, one k value per and in 3- dimension, one k value per .
The total number of modes in the crystal is calculated by multiplying the numbers of the density of modes by the reciprocal space value, which is taken by all wave vectors within the sphere whose radius is k. Therefore, the total number of modes N is,
Here, V is the macroscopic volume of the crystal, which is given by .
The debye model treats the crystal as an isotropic elastic medium, where the periodic pattern of atoms is the same. In this model, the wave vector is directly proportional to the frequency.
Where, is the velocity of sound acts as the proportionality constant here.This is similar to the dispersion relation in optics, where the speed of sounds takes the role of speed of light.
By using this relation, we can derive debye’s density of states. Substitute the value of k in (2),
The thermal vibrational energy is given by,
Where, is the Boltzmann distribution constant and h is the planck's constant.
Substitute the value of ,
The factor 3 represents the three different polarizations. One longitudinal and two transverse for each wave vector in the atomic lattice. The upper linmit is reduced from infinity to Debye frequency , the maximum frequency in the crystal lattice. This observation is given on the basis of one k per unit cell.
Therefore, the total numbr of modes becomes,
(6)
Hence, the cut off frequency is,
and
The corresponding wave vector is,
From the equation (5), substitute
Therefore, the vibrational energy is,
The Debye temperature in terms of Debye frequency is expressed as,
The Debye model of heat capacity is calculated easily by differentiating the vibrational energy with respect to the temperature.
In terms of Debye temperature,
Low temperature limit
The Debye temperature is said to be low, if the upper limit tends to infinity. This infinite integral is reduced to constant (convergent series).
which is the Debye approximation.
Therefore, the experimental observation of dependence of heat capacity at low temperatures is correctly proved.
High temperature limit
The Debye temperature is said to be high if, it is given by,
This is the Dulong-Petit law.
Einstein-Debye specific heat
At very low temperatures, the T dependence of specific heat agrees for nonmetals. And for metals, the specific heat of the atoms at high temperatures is defined by the Einstein model. The temperature dependence of the einstein model is just on T. Both Einstein model and debye model gives major contribution to the high temperature. To explain the low-temperatures specific heats of metals, they include electron contribution to the specific heat. The combined expression is given as,
Context and Applications
This is an important topic in solid-state physics and thermodynamics, for all the graduates and postgraduates, especially for
- Bachelors in science (physics and chemistry)
- Bachelors in technology (electrical engineering)
Practice Problems
Question 1: Phonons are ____.
a. Quanta of sound
b. Quanta of light
c. Quanta of energy
d. Quanta of heat
Answer: The correct option is a.
Explanation: Phonons are the quanta of sound waves. When energy is given to the atomic lattice, the lattice absorbs energy and gets excited to a higher energy level. While returning to the ground state, it emits radiation in the sound-wave region, which is known as phonons.
Question 2: The Debye temperature for silver is 225 K. Calculate the maximum frequency for lattice vibrations in silver.
Answer: The correct option is b.
Explanation:
Given data:
Debye temperature
Boltzmann constant
Planck's constant h=
The maximum debye frequency is derived from the debye temperature,
Substitute all the values,
Question 3: Find the specific heat capacity of sodium at 20K. The Debye temperature of sodium is 150K.
Answer: The correct option is c.
Explanation:
Given data:
Debye temperature of sodium .
The temperature of sodium T= 20K.
At low temperatures, Debye specific heat capacity is given by,
Question 4: The total number of polarizations in a sound wave in solid is______.
a. 1
b. 2
c. 3
d. 4
Answer: The correct option is c.
Explanation: There are 3 modes of polarisations in a sound wave. One is longitudinal mode and the other two are transverse mode.
Question 5: In the Debye model, the wave vector is proportional to______.
a. Frequency
b. Wavelength
c. Temperature
d. None of these
Answer: The correct option is a.
Explanation: In the debye model, the wave vector is directly proportional to frequency.
Where, is the frequency, k is the wave vector and is the proportionality constant (speed of sound).
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Debye Theory of Solids Homework Questions from Fellow Students
Browse our recently answered Debye Theory of Solids homework questions.