What is a wave?
Wave is an oscillation or disturbance traveling in a medium. It performs the transportation of energy but does not carry any matter. This motion of waves will transport fuel in a medium without permanent transfer of mass (particle).
Mechanical waves, electromagnetic waves, and matter waves are the three types of waves.
What is a mechanical wave?
A mechanical wave is a type of wave which needs a medium for propagation. It cannot travel through a vacuum. A mechanical wave is the outcome of the continuous periodic motion of particles in a medium. The disturbance occurring on one wave-particle transfers to the adjacent particle in that medium. Transverse waves and longitudinal waves are the two types of waves based on the direction of vibration of particles.
The daily life examples are the vibration of a string, oscillation of a spring, waves in slink, tsunami waves, etc.
Transverse wave
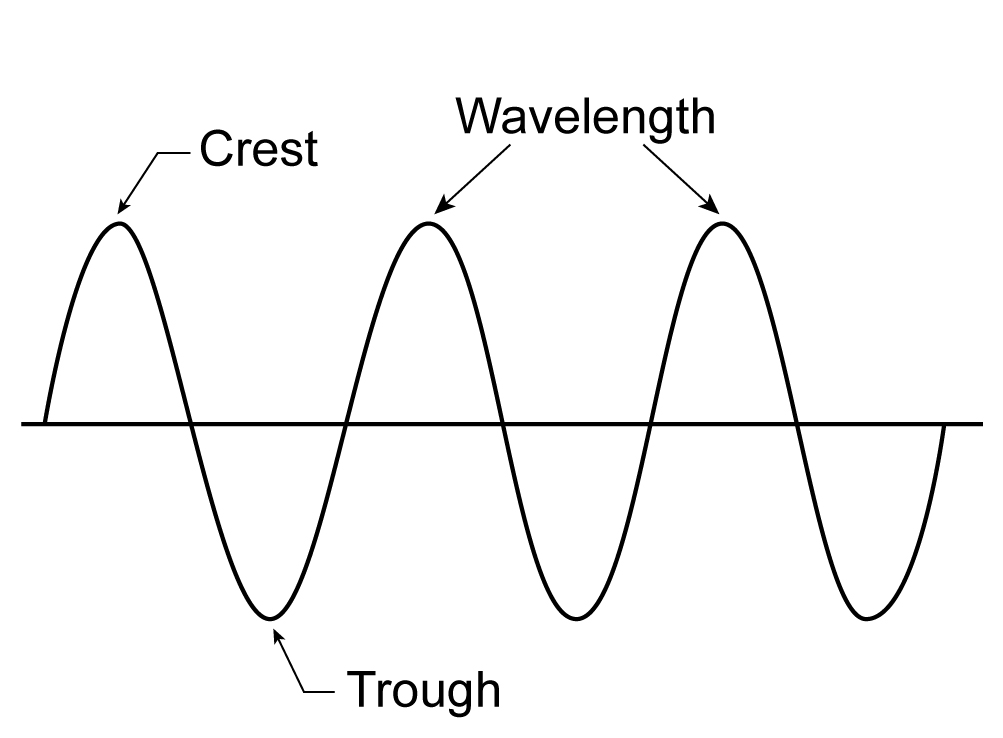
A transverse wave is the type of mechanical wave in which there is the vibration of the medium perpendicular to the direction of the propagating wave.
Examples of this kind of wave are water waves, radio waves, waves produced in strings, microwaves, etc.
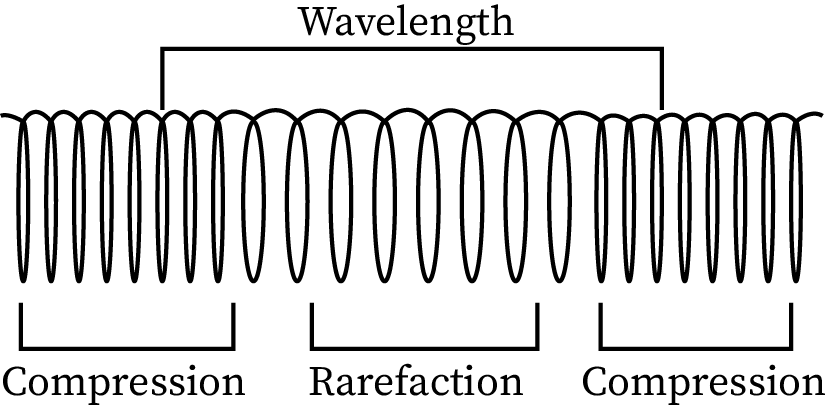
Longitudinal wave
A longitudinal wave is a mechanical wave in which medium particles' vibration is the same direction as the propagating wave. Here, the angle formed between the path of the wave-particle and the energy particle is zero. The portion of a longitudinal wave in which the particles are close together is called the compression region. The part in which the particles are apart is called the rarefaction region.
The two main examples of this kind of wave are sound waves and pressure waves.
Electromagnetic wave
An electromagnetic wave or EM wave is the type of wave that does not need a medium for transportation. It travels through a vacuum at the speed of light. Electromagnetic waves are due to electric and magnetic fields, and these waves show transverse nature. Examples of these waves are X-rays, ultraviolet waves, light waves, thermal radiations, etc.

The direction of an EM wave propagation is perpendicular to both the electric field vector and the magnetic field vector.
Matter wave
A matter-wave or Broglie wave is associated with any movement of an object. These waves are independent of the charge of the particles and they can travel through a vacuum. The properties of matter waves form the working principle of an electron microscope.
Properties of waves
The main properties of waves are amplitude, wavelength, frequency, time period, and velocity.
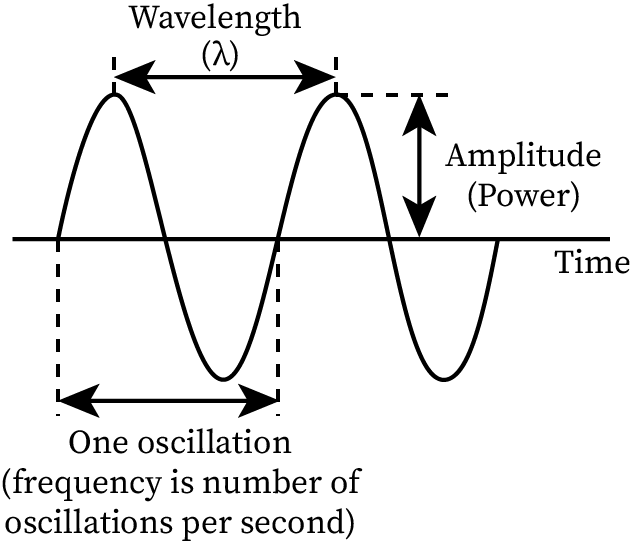
Amplitude
Amplitude refers to the maximum displacement of a particle. The energy carried by a wave is directly proportional to the amplitude of the wave.
Wavelength
The separation between two successive crests or troughs of a wave in a given medium is called its wavelength. The unit of wavelength is meter. It is denoted by λ. Wavelength is equal to the ratio of the velocity of the wave and its frequency. Its equation is as follows:
Frequency
The frequency of a wave is the number of waves produced per unit of time. Its S.I unit is Hertz (Hz).
Time period
Time taken by the wave to complete a single cycle is called its time period. The unit of the time period is in seconds and is the reciprocal of the wave's frequency.
Wave Speed/Velocity
Wave speed or velocity is the distance traveled by a wave in unit time. The wave equation for velocity is the multiplication of wavelength and frequency. The unit of both speed and velocity is m·s-1.
or
Wave equation for displacement
A traveling wave or a progressive wave travels continuously in a medium with the same direction and amplitude. The displacement of a wave along the Y-axis, at any time t and position x, is as follows:
Here, a denotes the wave's amplitude, ω refers to the angular velocity of the wave, k is the wave number, x is the displacement, and is the phase difference.
Phase of a wave
The phase of a wave is represented by . Phase signifies the position of the object under oscillation from the mean position. The waves traveling in the same direction are called in-phase waves, and those traveling in opposite directions are called anti-phase waves.
Wave number
The wavenumber of a wave represents its spatial frequency in terms of cycles per unit distance.
Angular frequency
The angular frequency of a wave is its angular displacement per unit time. The wave equation for angular frequency in terms of time period or frequency is:
Wave equation for standing waves
A standing wave or a stationary wave is the combination of two waves having the same frequency and amplitude, traveling in opposite directions. When these waves superimpose, their energies are either added or canceled.
Consider the equations of two waves; the first one moves in the positive X-direction and the other in the negative X-direction.
By the superposition principle, the combined wave equation is as follows:
Here, 2a sin(kx) is the amplitude of wave oscillation at the position corresponding to x. It will be zero when sin(kx) = 0 . (kx = nπ, where n = 1, 2, 3…)
The wave number is:
Then,
The displacement in the x-direction is:
The position of zero amplitude is called a node, and each node is separated by a length equal to half of its amplitude.
For the maximum amplitude of the wave, the value of 2a when sin(kx) = 1. This position is called an antinode.
Mathematical representation of electromagnetic waves
The wave equation of a plane electromagnetic wave traveling in the positive X-direction is as follows:
E(x,t)=cos (kx-ωt+ϕ)
B(x,t)=cos(kx-ωt+ϕ)
Here, E0 is the maximum amplitude of the electric field and B0 is the maximum amplitude of the magnetic field.
Wave speed in free space is:
Here, is the absolute permeability with the value and is the absolute permittivity.
What are one dimensional, two dimensional, and three dimensional wave equations?
In 1746, d’Alembert gave a one-dimensional wave equation. The conditions are mathematically represented as u(x,0)=f(x) and ut(x,0)=g(x), where x is the displacement along the X-direction having zero as the minimum value and the length of the string as the maximum value.
The mathematical equation for one-dimensional wave motion is:
Here, c is the wave speed with the value c=Tρ, ρ is the linear density, and T is the constant horizontal tension.
The two-dimensional wave equation also has the same initial conditions as the one-dimensional wave equation. The only difference is that they have an extra y-coordinate.
The two-dimensional wave equation is as follows:
Similarly, the represntation of a three-dimensional wave equation is:
Common Mistakes
Mostly, students get confused between transverse and longitudinal waves.
A transverse wave is the type of mechanical wave in which there is the vibration of the medium perpendicular to the direction of the propagating wave. A longitudinal wave is a mechanical wave in which medium particles' vibration is the same direction as the propagating wave. Here, the angle formed between the path of the wave.
Examples of transverse waves are water waves, radio waves, waves produced in strings, microwaves, etc., and examples of longitudinal waves are sound waves and pressure waves.
Context and Applications
This topic is significant for professional exams of undergraduate and postgraduate courses such as:
- Bachelor of Science in Physics
- Bachelor of Science in Chemistry
- Bachelor of Science in Atmospheric Science
- Bachelor of Science in Electronics
- Bachelor of Science in Disaster Management
- Bachelor of Technology in Electronics and Communication
- Master of Science in Physics
- Master of Science in Chemistry
- Master of Science in Atmospheric Science
- Master of Science in Disaster Management
Related Concepts
- Electromagnetic waves
- Schrodinger equations
- Dual nature of matter
- Electromagnetic spectrum
- Partial differential equations
- Oscillations
- Sinusoidal waves
Practice Problems
Q1. Which of the following mathematical equations represents an EM wave?
(a) E(x,t)=cos(kx-ωt+ϕ), B(x,t)=cos(kx-ωt+ϕ)
(b) E(x,t)=sin(kx-ωt+ϕ), B(x,t)=cos(kx-ωt+ϕ)
(c) E(x,t)=cos(kx-ωt+ϕ), B(x,t)=cos(kx+ωt+ϕ)
(d) E(x,t)=sin(kx-ωt+ϕ), B(x,t)=sin(kx-ωt+ϕ)
Correct option: (a)
Explanation: The correct mathematical equations represents an EM wave is E(x,t)=cos(kx-ωt+ϕ), B(x,t)=cos(kx-ωt+ϕ). Here E is the electric field vector and B is the magnetic field vector. Both vector includes cosine angles in their mathematical equations expression.
Q2. Which electromagnetic wave is responsible for maintaining the warmth of the Earth's atmosphere?
(a) Infrared waves
(b) Microwaves
(c) Ultrasonic waves
(d) Radio waves
Correct Option: (a)
Explanation: Infrared waves are responsible for maintaining the warmth of the Earth's atmosphere with the help of the greenhouse effect. When solar radiation comes on the surface of the Earth, some portion of the energy is being absorbed by the atmosphere and surface of our Earth, and therefore it hits the Earth's planet.
Q3. The highest point in the case of a transverse wave is called:
(a) Trough
(b) Crest
(c) Wave number
(d) Node
Correct option: (b)
Explanation: The highest point in the case of a transverse wave is known as crest. It is the highest point of a wave or hill. For example, the water will be achieving the highest point in the water stream. And the lowest point of any wave can be known as trough.
Q4. The distance between two adjacent crests or troughs of a wave is known as:
(a) Amplitude
(b) Frequency
(c) Wavelength
(d) Time period
Correct option: (c)
Explanation: Wavelength is the horizontal length between two adjacent points of a wave that is crest or troughs. The crest lies at the topmost point on the wave, while the trough is located at the bottom point of a wave.
Q5. Which of the following pairs has the same units?
(a) Wavelength, amplitude
(b) Velocity, amplitude
(c) Frequency, time period
(d) Amplitude, frequency
Correct option: (a)
Explanation: Wavelength and amplitude have the same units of measurement. Both can be measured in terms of meters as distance or length measurement. Velocity is measured in meters per second. Frequency is measured in hertz, and period/time is measured in seconds.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Equation of Waves Homework Questions from Fellow Students
Browse our recently answered Equation of Waves homework questions.