What is a frame of reference?
In physics, a frame of reference is a coordinate system used to specify either the position or the orientation or velocity of a body. The origin of the coordinate acts as a reference point for measuring the position or relative motion of a body. The coordinate system can be a cartesian coordinate, cylindrical coordinate, or a polar coordinate.
Importance of frames of reference
Consider an example where a person moves downwards in a lift. If the person throws an object towards the floor of the lift. What will be the velocity of the object? The velocity of the object differs as it is observed from a different point. The idea is that motion is relative, the description of motion depends upon the point of observation. For an observer outside the lift, the object will travel at a different speed. Hence it is important to assign a frame of reference before measuring the velocity or position or relative motion. There are two types of frames of reference. They are classified as inertial and non-inertial frames of reference.
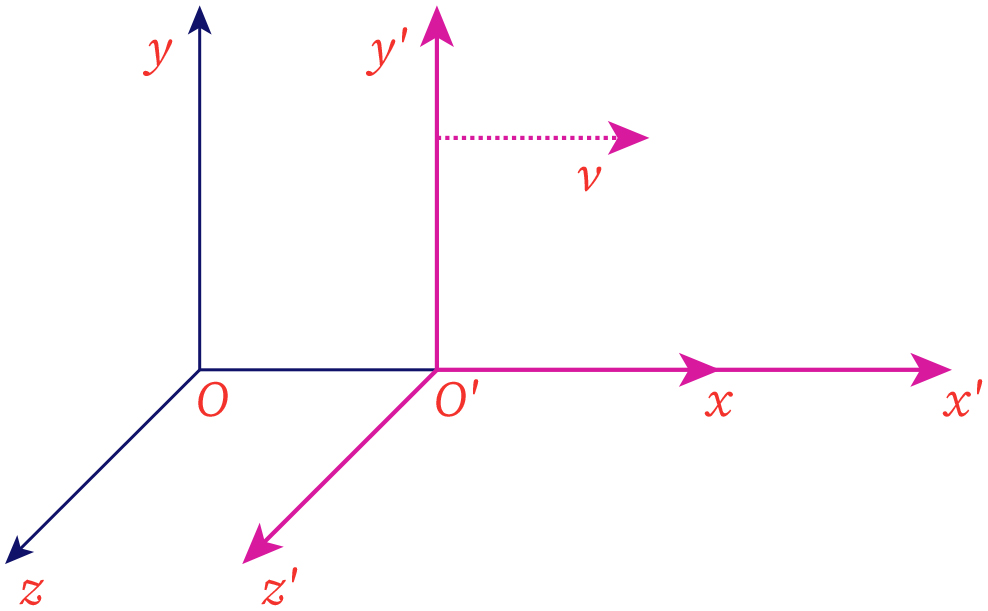
Inertial frame of reference
Inertial frames of reference obey Newton’s first law of motion. According to Newton’s first law, an object will be at rest or travel with constant velocity if there are no external forces acting on it. Therefore, in inertial frames, the net force exerted by the object is zero. In other words, the objects in inertial frames are not accelerated.
Hence, an inertial frame can either be at rest or travel with constant velocity with respect to another inertial frame of reference.
The non-inertial frame of reference
The non-inertial frame of reference is a frame that does not obey newton's first law. This means the in a non-inertial frame the object exerts a net force. Hence, the frame is accelerated with respect to an inertial frame of reference.
Now let us assume that the earth is an inertial frame. Since the moon travel with constant velocity with respect to earth; the moon cannot be an inertial frame. The motion of the moon is accelerated towards the earth with a force called centripetal force. The motion is accelerated if the direction of motion is changed. The direction of motion of the moon changes at every instant as it travels along an elliptical path as it exhibits uniform motion.
Transformation rules in classical mechanics
Say an object is studied with respect to a frame of reference. If we want to analyze the motion of the same object with a different reference frame, certain rules have to be followed. These rules are called transformation rules. In fact, the Galilean transformation rule is one of the important and fundamental rules in classical mechanics.
Galilean transformation rule for translation
Suppose consider a point particle that is traveling with a certain velocity. Let the P be the frame of reference with coordinates . Let us assume that the point particle is traveling along the x-axis with respect to the frame P. Consider a reference frame of reference P’ which is traveling along with the object relative to the rest frame. Let be the coordinates of frame P’. According to the galilean transformation rule, the frame P and P’ can be related using the following set of equations represents Galilean relativity.
Where,
v is the relative velocity of the object with respect to the frame P.
At time t=0, the coordinates of two frames coincide.
Transformation rules in modern physics
The classical Galilean transformations are not applied in modern mechanics. The important idea of classical mechanics is that time is absolute which means time is the same for every observer. But this is not the case in modern mechanics. The theory of relativity is based on the fact that time is not absolute or that time is relative. Time is different for observers moving at different speeds close to the speed of light. Hence classical transformation is not applicable to objects that are moving at a speed close to the speed of light. In this case, Lorentz transformation rules are used to transform from one reference frame to another.
Consider a point particle that is traveling with relativistic velocity v with respect to a rest frame P(x,y,z,t). If a dashed frame P’(x’,y’,z’,t’) is moving along x-axis with velocity v close to the velocity of light with respect to a rest frame. The frame P’ exhibits relative motion. The lorentz transformation rules are as follows:
where
Formulas
Galilean transformation rules are,
Lorentz transformation rules are,
where
v is the relative velocity of a point particle.
c is the velocity of light.
Context and Applications
This topic is significant in physics for both undergraduate and graduate courses, especially for Bachelors in physics, and Masters in physics.
Practice Problems
Question 1: Coordinate system is used in mechanics to determine _____.
(a) Position
(b) Velocity
(c) Momentum
(d) All of the above
Answer: Option (d) is the correct answer.
Explanation: In mechanics, the coordinate system is used to determine the base quantities like position, velocity, momentum, and energy. The coordinates are used to determine the magnitude of any physical quantity with respect to a reference point.
Question 2: A frame with ____ is not an inertial reference frame.
(a) Zero velocity
(b) Constant velocity
(c) Constant acceleration
(d) Net force is zero
Answer: Option (c) is the correct answer.
Explanation: The inertial reference frames obey newton’s first law of motion. Hence the net force exerted by the object at the inertial frame is zero. If the net force is zero then the object is either at rest or moving with constant velocity. If the velocity is constant then the acceleration is zero. Hence, constant acceleration is the correct answer.
Question 3: The classical transformation is not applicable for ____.
(a) Planets
(b) Rigid bodies
(c) Sound waves
(d) Photons
Answer: Option (d) is the correct answer.
Explanation: Classical mechanics is not applicable for particles or objects that travel with the velocity of light or close to the velocity of light. Since photons travel with relativistic velocity, the idea of classical transformation rules is not applied to photons.
Question 4: According to classical mechanics ____ is absolute.
(a) Time
(b) Position
(c) Velocity
(d) Energy
Answer: Option (a) is the correct answer.
Explanation: The base assumption of classical mechanics is that time is absolute. This means time is the same for all the observers irrespective of their motion. Hence, option (a) is the correct answer.
Question 5: The motion of the moon around the earth is a non-inertial reference frame because____.
(a) The velocity is constant
(b) The motion is accelerated
(c) The net force is zero
(d) None of the above
Answer: Option (b) is the correct answer.
Explanation: The moon revolves around the earth with constant velocity but the motion is non-inertial because the moon is accelerated towards the earth due to a force called centripetal force. Hence, based on the fact that the motion exerts force, the motion is accelerated. Option (b) is the correct answer.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Frame of reference Homework Questions from Fellow Students
Browse our recently answered Frame of reference homework questions.