What is Power?
Power is defined in physics as the amount of energy transmitted or transformed per unit time. The watt is the unit of electricity in the International System of Units, equivalent to one joule per second.
Power
Power is often referred to as movement in older books. Power is defined as a scalar quantity. A motor's output power is the product of the torque produced by the motor and the angular velocity of its output shaft. The power used to move a ground vehicle is the combination of the traction force on the wheels and the vehicle's velocity. In statistical physics, the motive power of an aircraft vehicle is calculated as the sum of engine thrust and vehicle velocity from a stationary frame of reference.
In classical mechanics, the motive power of a jet-propelled vehicle is calculated as the product of engine thrust and vehicle velocity from a stationary understanding of reality. Watts the amount of electrical energy consumed per unit of time are used to calculate the rate with which a light bulb transforms electrical energy into light and heat.
Concept of Power
Power is given by the time derivative of work.
Power,
The unit of power in the International System of Units (SI) is the watt (W), which is equal to one joule per second. Other popular and standard metrics include horsepower (hp), which compares to horsepower; one mechanical horsepower equals approximately
Types of Power
Mechanical power
One metric horsepower is needed to lift 75 kilograms by 1 metre in 1 second. Power in mechanical systems is the combination of forces and movement (product of force and velocity). It can also be found by taking the derivative of work with respect to time.
Electrical Power
It is further classified based on power source one uses direct current ( DC power ) or alternating power
For DC circuits: Power consumed in a DC circuit is essentially the output of DC voltage times DC current, expressed in watts. Nevertheless, for alternating current circuits with reactive elements, we must quantify absorbed power differently. Since electrical power is the rate at which electricity is absorbed in a circuit, both electrical and electronic components and systems have just a cap on the amount of electrical power that they would safely accommodate.
Electrical power could be time-varying either as a direct current (DC) quantity or as an alternating current (AC) quantity. The sum of power in a circuit at any given time is referred to as instantaneous power, and it is calculated using the well-known equation power equals volts times amps
So, one watt (the rate at which electricity is expended at one joule per second) is equal to the volt-ampere product of one-volt times one ampere.
For AC circuits: Because there is no sinusoidal waveform associated with the source, the voltages and currents in a DC circuit are usually constant, that is, they do not change with time. In an alternating current circuit, though, the instantaneous values of voltage, current, and hence power are continuously changing and are determined by the source. So, while we cannot quantify power in AC circuits in the same way as we can in DC circuits, we can also assume that power equals voltage times current .
Some other crucial thing to remember is that AC circuits have reactance, which means that there really is a control component as a result of the magnetic and/or electric fields generated by the components. As a consequence, unlike a strictly resistive component, this power is retained and then transferred to the supply as the sinusoidal waveform completes a full periodic loop.
As a result, the average power consumed by a circuit is the amount of power accumulated and power returned over one full loop. Thus, the average power consumption of a circuit is the average of the instantaneous power over one complete cycle, with instantaneous power (i.e. instantaneous voltage x instantaneous current).
Instantaneous power in electricity is given as product of current and voltage.
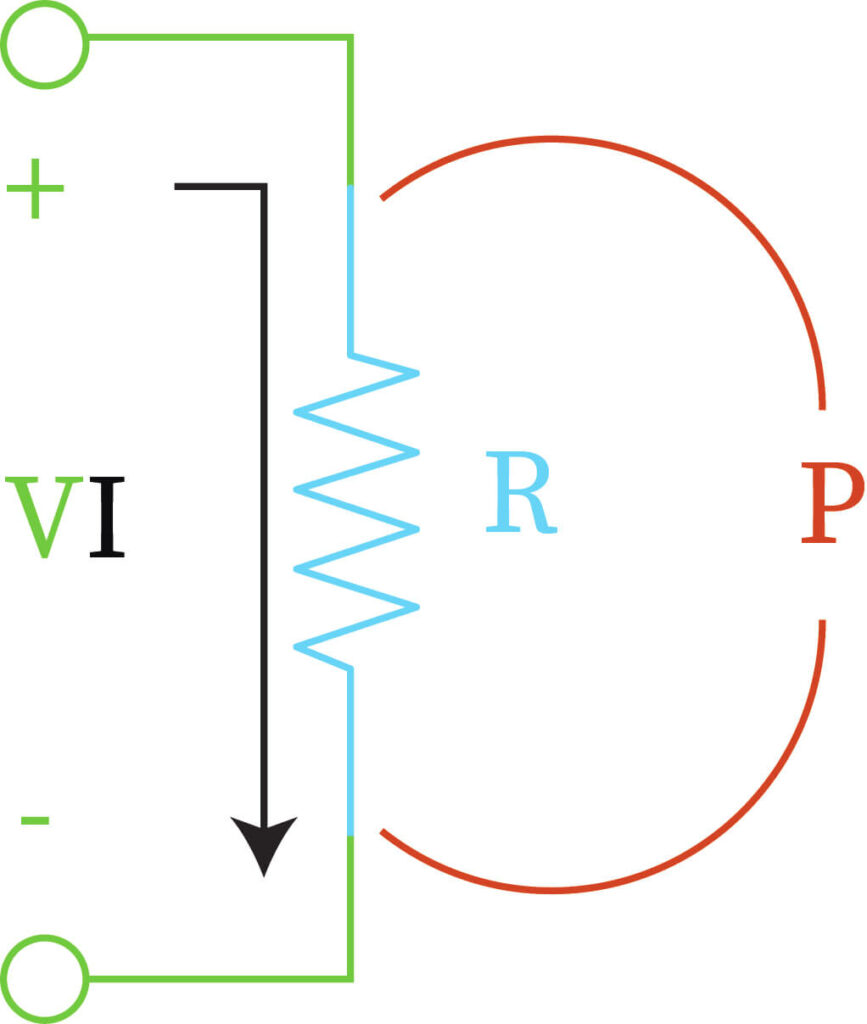
In an electric circuit, instantaneous power is the rate at which electricity flows past a given point in the circuit. In alternating current circuits, energy storage elements such as inductors and capacitors may cause periodic reversals of energy flow path.
Active power is the portion of power that, when multiplied over an entire period of the AC waveform, results in a net shift of energy in one direction (more commonly called real power to avoid ambiguity especially in discussions of loads with non-sinusoidal currents).Instantaneous reactive power is the portion of power attributable to stored energy that returns to the source in each loop, and its magnitude is the absolute value of reactive power.
This equation demonstrates that the instantaneous alternating current power has two distinct components and is thus the sum of these two terms. Due to the 2 components of the definition, the second term is a time changing sinusoidal with a frequency equal to twice the angular frequency of the supply.
The first concept, on the other hand, is a constant whose value is determined solely by the phase difference between the voltage and the current.
Active, Reactive, and Apparent Power
Current and voltage are also sinusoidal in a simple alternating current (AC) circuit consisting of a source and a linear load. As a strictly resistive load is applied, two quantities change their polarity at the same time. Since the product of voltage and current is either positive or zero at any given moment, the direction of energy flow does not reverse. Only active control is transferred in this situation. When the load is fully reactive, the voltage and current are 90 degrees out of phase. The product of voltage and current is positive for two-quarters of each loop, but negative for the other two quarters, meaning that on average, just as much energy flows through the load as flows out. For each half cycle, there is no net energy supply. Only reactive force flows in this case: There is no net energy transfer to the load; however, electrical power flows along the wires and returns in reverse along the same wires. Even if the optimal load system absorbs no electricity, the current needed for this reactive power flow dissipates energy in the line resistance. Since practical loads have resistance as well as inductance or capacitance, typical loads may receive both active and reactive control.
The apparent power is the product of the rms voltage and current values. Apparent power is included when planning and running power systems because, even though current associated with reactive power does not do any function at the load, it must also be provided by a power source. Conductors, transformers, and generators must be sized to bear absolute current, not just usable current. Failure to provide adequate reactive power in electrical grids can result in lower voltage levels and, under some operating conditions, network breakdown or outage. Another implication is that combining the obvious force for two.
Power Quality
The degree to which the voltage, frequency, and waveform of a power supply system correspond to specified requirements is referred to as electric power efficiency. A steady supply voltage that remains within the specified range, a steady A.C. frequency that is equal to the rated value, and a smooth voltage curve waveform are both indicators of good power efficiency. In common, power quality can be described as the reliability between what emerges out of an electrical outlet and the load that is plugged into it. The definition refers to the electric power that powers an electrical load as well as the load's ability to work efficiently. An electrical device (or load) can overload, fail prematurely, or not work at all if not supplied with adequate power.
Average Power(P)
The average power is the power delivered to the load and dissipated by the load.
Here, is rms voltage, is rms current and is phase angle.

Practice Problem
Question 1: In an ultrashort pulse laser machine, produces a pulse of time period ( 1 fs is equal to ), the peak power recorded by the device is , which is roughly the average power required by 100 houses. If the layer given is 1000 pulse per sec by the machine, then find out the average power output required by the machine?
Solution:
Calculate the average power output required by the machine :
Here, P is power produced by device and t is pulse time period.
Substitute, for and for in Equation (2).
Substitute, for and for in Equation (1).
Therefore, average power output required by machine is
Question 2: Car has a mass of 1000 kg and has power output to the wheels of 75 KW. The claims that it has constant acceleration over the range of 0-25 m/s. Calculate the time acceleration for claimed power.
Solution:
Power is represented by an equation that relates work and time. Although we recognize that forces do work and also that forces will drive objects, we would think that learning the strength would help us to learn much more about motion of a body over time.
Calculate the time acceleration for claimed power (t):
……(1)
Here, is average power, is mass, is acceleration, is final velocity and is initial velocity.
Since, is .
……(2)
……(3)
Since, is .
Substitute, for in Equation (2).
Substitute, 1000kg for m , 75000kW for Pavg and 25m/s for Vfinal/2 in Equation (4).
Therefore, the time acceleration for claimed power is 4.17s.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Science in Physics
- Masters in Science in Physics
- Bachelors in Engineering Mechanical.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Instantaneous Power Homework Questions from Fellow Students
Browse our recently answered Instantaneous Power homework questions.