What is Work-Energy?
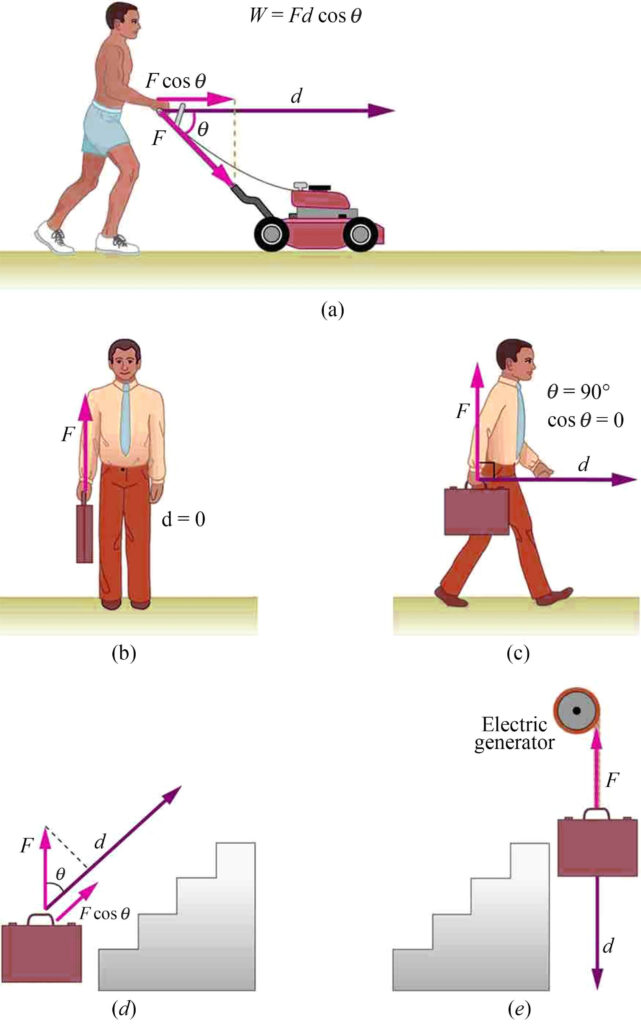
In physics, work is the product of the net force in direction of the displacement and the magnitude of this displacement or it can also be defined as the energy transfer of an object when it is moved for a distance due to the forces acting on it in the direction of displacement and perpendicular to the displacement which is called the normal force. Energy is the capacity of any object doing work. The SI unit of work is joule and energy is Joule. This principle follows the second law of Newton's law of motion where the net force causes the acceleration of an object. The force of gravity which is downward force and the normal force acting on an object which is perpendicular to the object are equal in magnitude but opposite to the direction, so while determining the net force, these two components cancel out. The net force is the horizontal component of the force and in our explanation, we consider everything as frictionless surface since friction should also be calculated while called the work-energy component of the object. The two most basics of energy classification are potential energy and kinetic energy. There are various kinds of kinetic energy like chemical, mechanical, thermal, nuclear, electrical, radiant energy, and so on. The work is done when there is a change in energy and it mainly depends on the application of force and movement of the object. Let us say how much work is needed to lift a 5kg ball 5m high. Work is mathematically represented as Force ×Displacement. So it will be 5kg times the gravitational constant on earth and the distance moved by the object. Wnet=Fnet times Displacement.
What is Kinetic Energy?
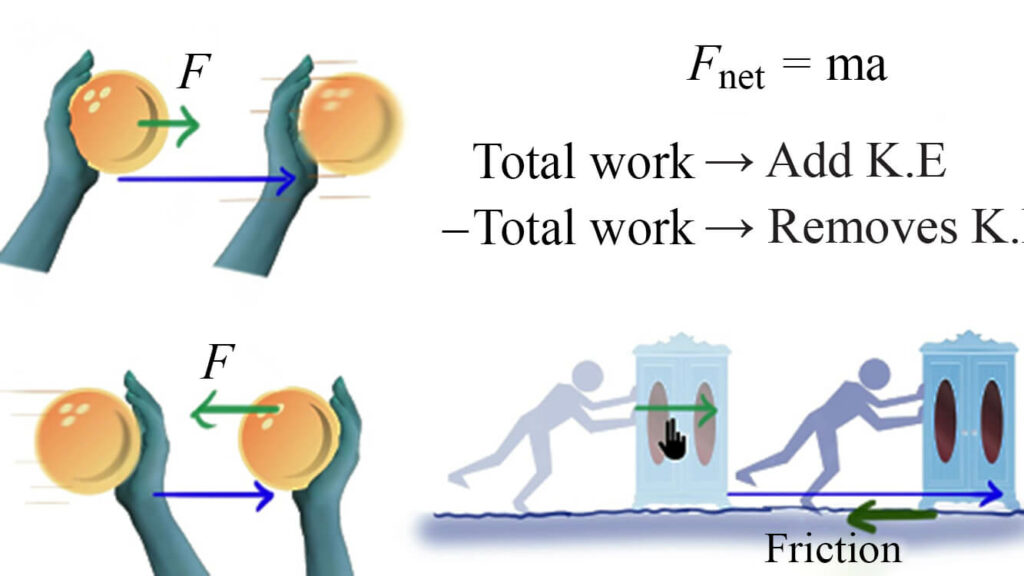
Force on an object causes its acceleration and only if the force is applied then work is done and the energy is transferred. When work is done the object gets accelerated and moves at a speed and this energy that is making the object move is called kinetic energy which merely depends on the mass and velocity of the object. It is the measure of the net work done on the object due to the virtue of its motion. The kinetic energy is a scalar quantity and its SI unit is kg.metre2.second2
The equation of the kinetic energy is
Principle of Work-Energy Theorem
In physics, the work-energy theorem defines that the work done by the sum of all forces which is called the Fnet on a particle present in the object is equal to the kinetic energy of the particle. It is applicable for all the rigid bodies even moving in a uniform circular motion where the work done is torque and the energy needed to keep in its motion is the rotational kinetic energy. The mathematical equation stating the relation between the Work-Kinetic energy can be done by linking both the equation of work and kinetic energy.
The work done is;. The force is defined as the product of acceleration and mass of the object.
The acceleration of the work-energy theorem equation to be used depends on the square of the differences of the initial velocity and final velocity and the distance traveled by the object. Let the initial velocity be denoted as Vinitial and the final velocity be represented as Vfinal
So the equation of the work will be modified to be
Hence the work done by the object gives the Work-Energy theorem equation as the difference between the final kinetic energy and initial kinetic energy so
The above equation can also be modified or simplified where the difference between the initial kinetic energy and final energy can be denoted as
In physics, The work-energy theorem representing it as vector components can be defined as the object moveing due to the force component F though a displacement Δd which is equal to the component of the force parallel to the displacement vector Δd times the scalar component of the displacement. Now the velocity vector will be used here to describe the equation but the kinetic part of the energy still remains scalar. Here the net force is the different from the scale component of the work done. The net force is the vector sum of all the forces acting on a object and the total work is sum of all the work done on or by the object. Positive work is when the work is done on the system or an object. Positive work is when the force component is parallel to the system. Negative work is when the work is done by the system. Negative work is when the force component is against the displacement
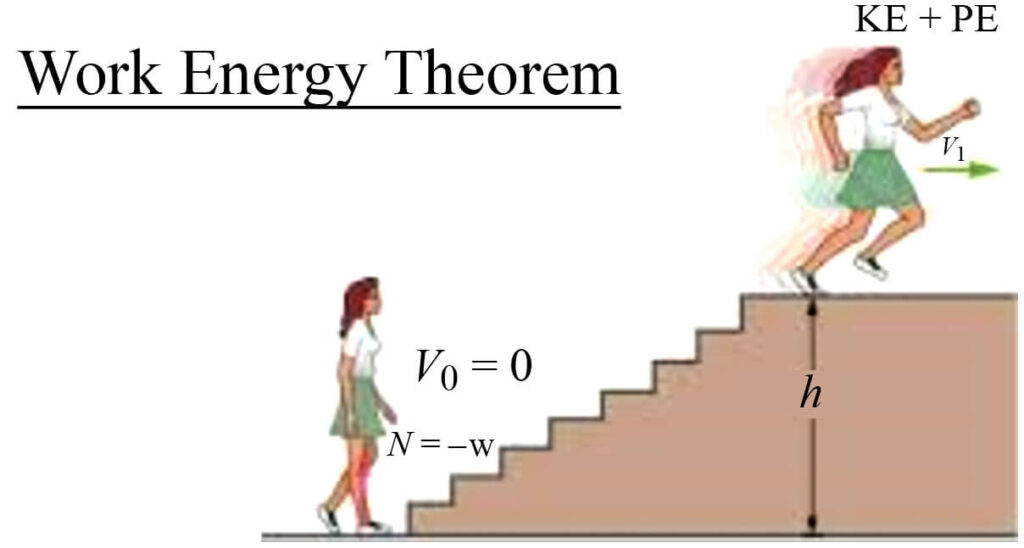
Conservation of Work-Energy Theorem
This law of conservation of the work-energy theorem states that any system that has a total energy E, remains constant and it is additive in nature. It is the sum of the total kinetic energy exerted by the system and sum of the total potential energy stored in the system. It is mathematically
represented as and the potential energy is mgh. So the conservation of the work-energy equation will be
. The classic example of the conservation of energy is when we give an external force to a simple pendulum and when the bob attached starts moving from its its rest or equilibrium position.
Application of Work-Energy Theorem
1) After understanding the theorem, there is a strong relation between work and energy which forms one of the fundamental units in Physics. So it is used in understanding the physics behind the oscillation of pendulum.
2) It helps us understand the use of potential energy in a system and the capacity of a system especially in thermodynamics and mechanical engineering.
3) It helps us to analyse the working of spring, its compression and expansion mechanics when it is connected to a rigid body.
4) It is vastly used in understanding the linear and nonlinear rotational dynamics of objects moving in a circular motion.
Practice Problem
1) State few examples of the work done by us in our daily routine. Analyse how the entry transfer occurs. When is the work done by a system and when is the work done on the system. Give example for both types of work.
2) Calculate the work done on a 1500 kg elevator by its cable to lift it 40 m at a constant speed, assuming friction averages 100 Newton. What is the work done on the lift by the gravitational force in this process? What is the total work done on the lift?
Context and Applications:
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science in Physics
- Master of Science in Physics
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Kinetic Energy and Work-Energy Theorem Homework Questions from Fellow Students
Browse our recently answered Kinetic Energy and Work-Energy Theorem homework questions.