What is Magnification?
In very simple terms, the same object can be viewed in enlarged versions of itself, which we call magnification. To rephrase, magnification is the ability to enlarge the image of an object without physically altering its dimensions and structure. This process is mainly done to get an even more detailed view of the object by scaling up the image. A lot of daily life examples for this can be the use of magnifying glasses, projectors, and microscopes in laboratories. This plays a vital role in the fields of research and development and to some extent even our daily lives; our daily activity of magnifying images and texts on our mobile screen for a better look is nothing other than magnification.
Lateral Magnification
There are various types of magnification but in this lesson, we will focus on lateral magnification.
Before we jump right into the topic some general terminologies need to be understood.
- Optical centre: It is the central point of the lens, where the optical axis and principal axis intersect.
- Optical axis or vertical axis: A vertical line passing through the centre of the curvature of a lens.
- Object distance: It is the distance between the optical centre and the object.
- Image distance: It is the distance between the optical center and the image formed.
Lateral magnification, also known as linear or transverse magnification, is the ratio of the height of the image to the height of the object.
Lateral Magnification for a Lens
When an object is placed on one side of the lens, the image formed on the opposite side appears to differ in size compared to the object. The image is then called to be magnified. To find the value by which the image is magnified, we use a formula that is derived by the definition of lateral magnification.
Where m=magnification, hi = height of the image and ho = height of the object
This is a dimensionless (unitless) quantity as the numerator and denominator has the same dimension which cancels out each other.
The quantity lateral magnification can also be calculated using its relationship with the image distance and object distance. The equation is as follows
Where m = magnification, -ox’ = the image distance and ox = the object distance
If the value of the lateral magnification is one, the size of the image and object are the same. If the value of the lateral magnification is greater than one, the image is enlarged. And if lateral magnification is less than one, the image is diminished.
If there is a positive magnification, the image formed is virtual (the image formed is erect) but if the magnification is negative the image formed is a real image (the image formed is inverted).

Lateral Magnification of Concave Mirrors
For real and inverted images: if the object is placed beyond one focal length of the mirror the image formed is a real image and therefore the height of the image will be negative. This will result in the magnification also being negative. Furthermore, the magnification size will depend on the placement of the object on the principal axis.
For a virtual and erect image formation: When the object is placed within the focal length of the mirror the image formed is an upright virtual image. This is why the height of the object is considered positive and so will the value of magnification be positive.
For both cases, the same general equation (height of object divided by height of the image) is used to calculate the lateral magnification.
Lateral Magnification of the Convex Mirror
The image formed by a convex mirror is always virtual and erect. This is why the height of the object is considered positive and so will the value of magnification be positive.
For this case too the same general equation (height of object divided by height of the image) is used to calculate the lateral magnification.
Lateral Magnification of an Image formed at a Spherical Surface by Refraction
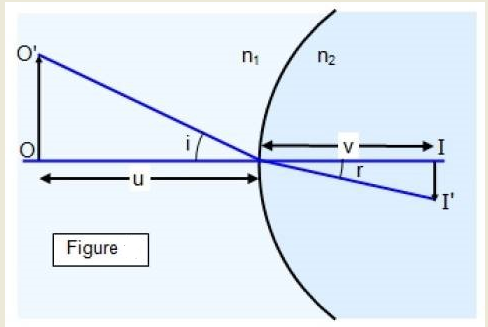
Referring to the image attached above we will first understand the diagram and the labeling of such diagrams. These are the representations that are used in this lesson but there is no hard and fast rule for the same.
- To start with the O indicates the position of the object and I indicates the position of the image formed after refraction.
- The line passing straight through the object, the lens and the image without bending (x-axis) is known as the principal axis.
- The centre is the point at which the principal axis intersects the curvature of the lens.
- v is the distance between the optical centre and the image and u is the distance between the optical centre and the object
- i is the angle of incidence of the light ray and r is the angle of refraction of the light ray
- O:O’ is the height of the object. Similarly, I:I’ is the height of the image formed
- n1 and n2 are the respective indexes of refraction in the medium.
We can assume that i and r the angles are small which means less than a 1 radian, for parallax rays.
Using this approximation, we get two equations for the two angles
There is a minus sign used before the height of the image as the image formed is a real image which means it is inverted. So, the height of the image will be less than 0 but the angle r is a positive angle.
To solve this further we will use the concepts of Snell’s law which are as follows
Using the two equations we obtained above we derive a new equation by merging the two
Therefore the equation of lateral magnification which is given in terms of height can now be written in terms of index of refraction and image distance and object distance
Common Mistakes
- Correctly identify the nature of the image otherwise the sign conventions will go wrong.
- Remember every formula, or remember one and learn how to derive the others using that.
- Be familiar with the common labeling methods of the ray diagrams
Related Concepts
- Converging lens
- Diverging lens
- Index of refraction
Context and Applications
This topic is studied in secondary and senior secondary classes as well as Bachelors in Science (Physics)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Lateral Magnification Homework Questions from Fellow Students
Browse our recently answered Lateral Magnification homework questions.