What is Oscillation?

In Physics, oscillation means a repetitive motion that happens in a variation with respect to time. There is usually a central value, where the object would be at rest. Additionally, there are two or more positions between which the repetitive motion takes place. In mathematics, oscillations can also be described as vibrations. The most common examples of oscillation that is seen in daily lives include the alternating current (AC) or the motion of a moving pendulum.

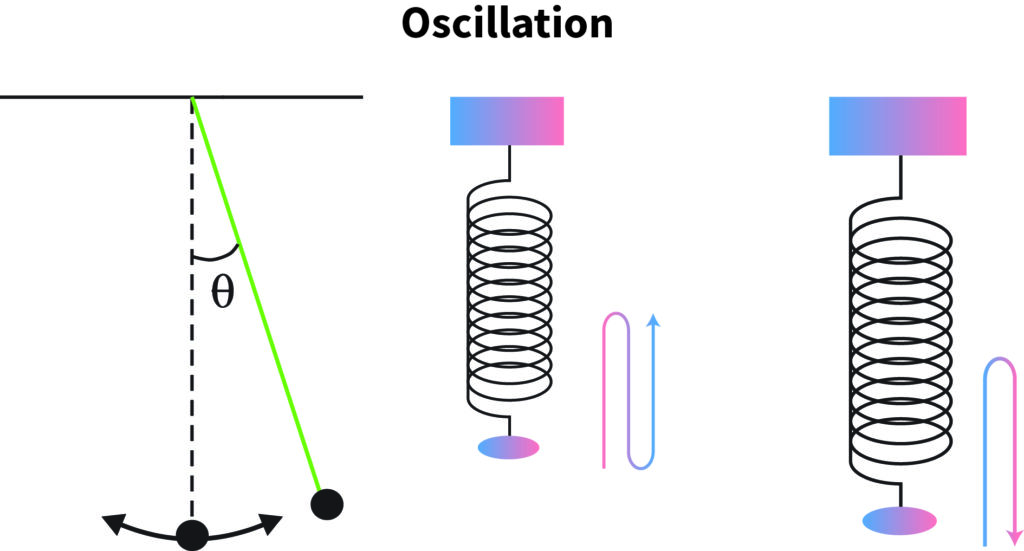
How does Oscillation Work?

Usually, an object can move within two or more final positions from a single initial position. When this motion is repetitive, and there is a variation in every motion, it is known as oscillation. However, oscillation is a broad term which includes vibration, motions that occur in fixed time intervals, and harmonic motions as well.

What are the types of Motion in Oscillation?

In oscillation, there are usually three main types in which motion takes place. They are-

• Periodic Motion
• Oscillatory Motion
• Simple Harmonic Motion

The types of motions have been discussed in details below

What is Periodic Motion?

In periodic motion, an object moves within a fixed path, and the motion continues after a fixed time interval, or as the name suggests, in a fixed period. Here, the path of the motion needs to be the same, and the time period after which the motion is repeated needs to be the same too. The time interval or the period after which the object performs the periodic motion is described as the ‘Harmonic Motion Period’ or ‘T’.

There is no restriction regarding what path should the object in question be in motion. For instance, the path can be shaped like any curve, or it can be elliptical, circular, or linear. As long as the path remains constant and the period remains fixed, the motion will be periodic. The displacement in a periodic motion is usually in a wave form.

What is Oscillatory Motion?

By oscillatory motion, it means an object which undergoes motion in a vibrating pattern. Usually, the to and fro motion is used to describe the oscillatory motion. It basically means that the oscillator has a fixed initial position or equilibrium position at rest, and while in oscillatory motion, it moves on both sides of the resting position in a to and fro manner. When particles oscillate, the positions up to which the particles can move to either side of their initial positions are known as the extreme positions or final positions.

In an oscillatory motion, the extreme positions need not be always fixed. It is not necessary for oscillatory motions to be periodic. In fact, in real life situations, the distance from the initial position to the extreme position and the period of motion becomes shorter and shorter as the motion continues. This is because there is a loss of energy when the motion takes place. In an oscillatory motion, a force acts in the direction of the initial position of the object. This force, or torque to be precise, is the reason why the oscillator in motion can undergo the oscillation. This torque is also known as the force of restoration or restoring force. When a pendulum moves, the torque directs the pendulum back to its mean position.

What is Simple Harmonic Motion?

A simple harmonic motion, also known as SHM, is a special type of oscillation where the force of restoration is directly proportional to the displacement of the object from its mean or initial position. This hinders the increase in the object’s displacement while it is in motion.

In other words, if an object is in motion such that the acceleration of the object is directly proportional to its displacement, and which helps the moving object to return to its resting position, then the object is said to undergo a simple harmonic motion. An object undergoing SHM always moves like a wave.

What are the necessary conditions for SHM to take place?

For a simple harmonic motion to happen, there are some necessary conditions. They are as follows-

• A stable equilibrium position must exist for an object undergoing SHM. When the object is exactly as this position, then the object has the minimum potential energy.

As a result-

Here, U is the potential energy, and y is the displacement of the object.

• In SHM, there will not be any energy dissipation taking place.
• Also, the acceleration of the object in SHM is in the oppose direction of displacement, and it is directly proportional to displacement as well.

Hence,

Here, the acceleration is a, ω denotes the angular frequency, and the negative (-) sign denotes the opposite direction.

Formula

The SHM equation can be denoted by the formulas as follows-

Here, F is the force and k is the constant.

Displacement

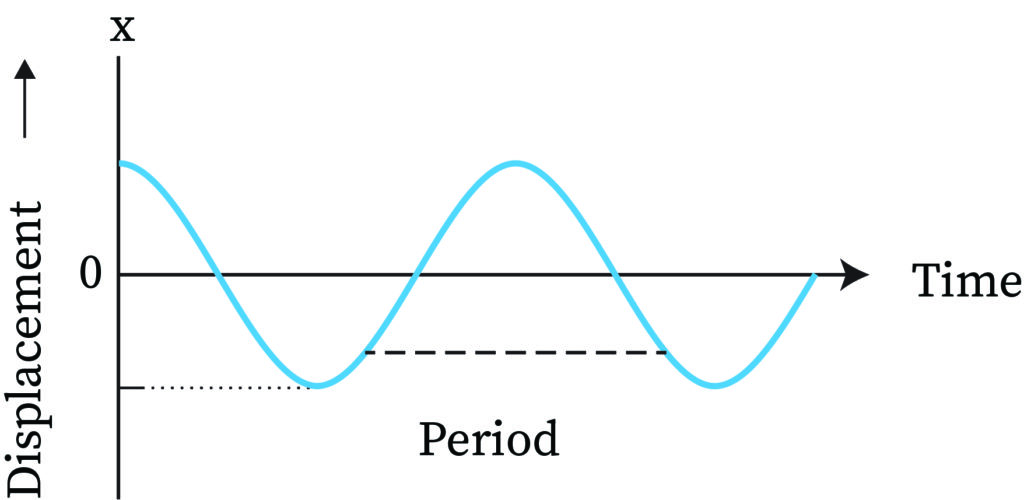
The displacement in SHM is denoted by ‘y’. In any time, when an object undergoes SHM, its position can be defined as the distance between the object at that point from its initial or mean position.

It can be expressed as-

Here, r is the circle’s radius or the amplitude, and ϴ is the phase.

It has been seen that when ϴ becomes zero, y equals r sin ωt. Also, when ϴ equals π/2, y becomes r cos ωt.

Amplitude

The amplitude of an object moving in SRM can be said to be the maximum distance that the object can be displaced from either side of the initial position. It is denoted by r.

Velocity

The velocity of an object undergoing SHM is denoted by V, and it is denoted as-

Here, the object’s linear velocity is denoted by v.

If y becomes zero, then V equals v, which further equals to rω. Also, V becomes zero when y equals ± r.

In an object undergoing SHM, its velocity becomes zero at the extreme positions, and the velocity becomes maximum when the object passes through its mean position.

It can also be expressed as-

Acceleration

In an oscillating object undergoing SHM, the acceleration is the rate of change of its velocity. It is denoted by ‘a’, and it can be expressed as-

If y becomes zero, then acceleration becomes zero as well. Similarly, if y equals ± r, then acceleration equals ± ω²r.

When the object just passes its mean position, it has acceleration = 0. At the extreme positions, the object acquires its highest acceleration. The force of acceleration is always on the direction of the object’s mean position. Also, the acceleration has a direct proportion to its displacement.

Time period

The time period is denoted by T, and it is the time than the object in motion takes for completing a single movement along its path before repeating the same movement again.

It can be denoted as –

Frequency

It is denoted by f, and it means the number of vibrations that the object in motion can perform under exactly 1 second.

It can be denoted as –

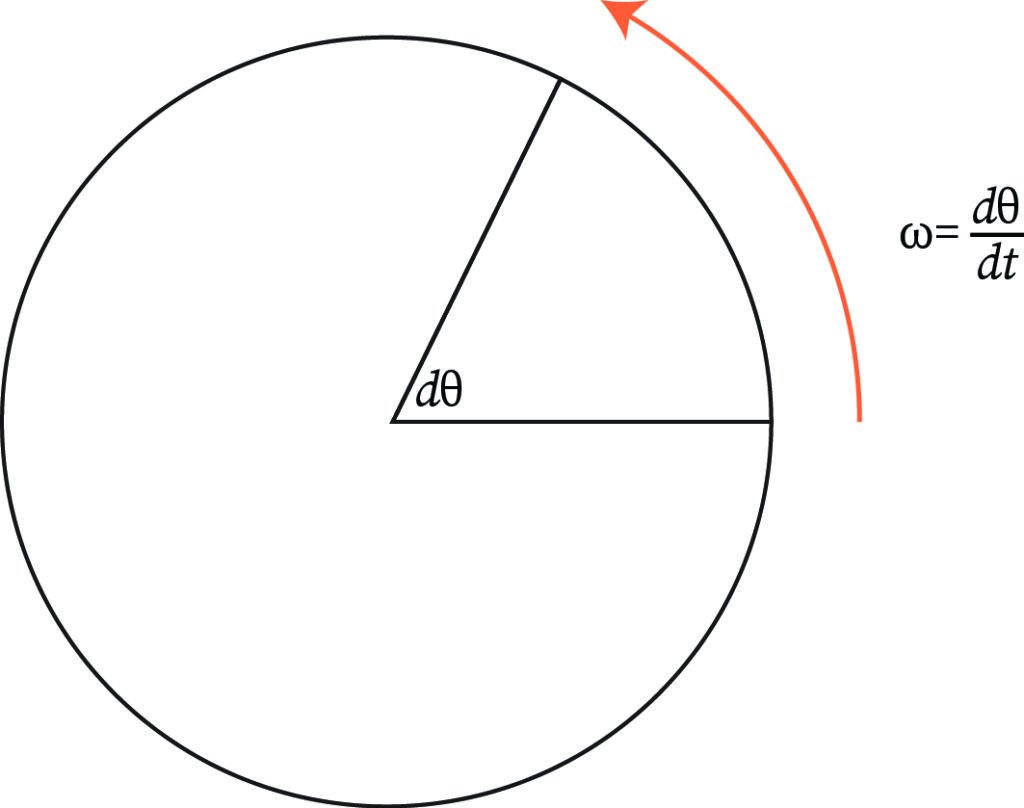
Angular Frequency

If the frequency is expressed in radian per second format, then it is known as angular frequency of the object in motion. It is denoted by ω.

It can be expressed as –

The angular frequency can be obtained by simply multiplying the frequency with 2π. In other words, ω = 2πf.

Phase

For an object undergoing oscillation, the phase is the state of the object with respect to the motion’s direction, and the object’s position. It is usually measured with respect to angle, and denoted in the form of a fractional part of 2π radian. This measurement is taken when the object in motion has just crossed its initial position, and is headed towards the positive direction.

Practice Problem

If the frequency of an object under SHM is 1.4 Hz, find its angular velocity.

⇒ Here, f = 1.4 Hz.

Using ω = 2πf,

Therefore, the angular frequency ω is 8.8 radians per second.

Context and Applications  

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for  

• Bachelors in Science Physics 
• Masters in Science Physics