What is quantum mechanics?
Quantum mechanics is a branch of modern physics that deals with the behavior of matter and energy and on the microscopic scale, i.e., on the scale of atoms or sub-atoms. Quantum mechanics use Planck's Quantum theory and de Broglie's hypothesis to explain certain properties of matter and energy. These concepts are based on the Schrödinger equation. In quantum mechanics, the solution of the Schrödinger equation provides information about energy levels and line spectra of hydrogen and hydrogen-like atoms. Schrodinger's equation also gives the probability of finding an electron at any point in a particular atom.
What is Bohr's second postulate of quantization?
An atom of hydrogen contains an electron and a proton and does not contain neutrons. According to the second postulate of Bohr’s model of a hydrogen atom, the electron revolves around the nucleus only in certain discrete orbits for which the total angular momentum of the electron (L) is quantized, i.e.,
Here, m is the mass of the electron, r is the radius of the orbit, v is the velocity of the electron, h is Planck's constant, and n is any positive integer called the principal quantum number.
Schrödinger equation
Consider an electron of mass m moves with the velocity v in a hydrogen atom. If an electron is at a distance r from the proton, then the potential energy function of the electron can be written as follows:
Here, -e is the charge of an electron, +e is the charge of a proton, and k is the electrostatic force constant.
In three dimensions, the time-independent Schrödinger wave equation can be written as follows:
...(1)
The solution of the Schrödinger equation is which is known as the wave function of the electron. The wave function of a particle provides the complete quantum mechanical description of that particle.

Since potential energy function V(r) depends on r, and the atom is spherical; therefore equation (1) should be converted into spherical polar coordinates, i.e., wave function ψ should be the function of r,θ,ϕ such that
Here, are the polar angle and azimuthal angle, respectively. The spherical polar coordinates of a point K are shown in the figure above.
Thus in terms of spherical co-ordinates, equation (1) can be written as:
... (2)
Equation (2) is a partial differential equation solved by using the method of separation of variables.
If the wave function is a product of three different functions i.e., , then on substituting this value of wave function in the Schrödinger equation (2) and using the method of separation of variables, we get three independent differential equations each depending on only one variable. These three differential equations are as follows:
...... (3)
...... (4)
...... (5)
Here, A and B are the seperation constant.
Azimuthal equation
Equation (5) is the simplest form known as the azimuthal part of the Schrödinger equation. The value of constant B is .
The solution of the differential equation (5) is of the form,
The boundary condition gives and the valye of should be zero at any integer whether positive or negative.
Angular equation
Equation (4) is known as the angular part of the Schrödinger equation that results in A = l (l+1), where the values of l and are as shown below.
l=0,1,2,3,4,....
=-l,-l+1,-l+2..........l-2,l-1,l
Radial equation
Equation (3) is called the radial part of the Schrödinger equation. On putting values of A and B, equation (3) will become
. ...(6)
The above differential equation is called the radial equation. Sometimes, this equation is also referred to as the associated Laguerre equation.
Solution of the Schrodinger equation
The solution of the Schrödinger equation (2), i.e., the wave function is as follows:
The solutions f(θ) of the angular equation and of the azimuthal equation depend on the value of ml and thus can be grouped into a single function known as the spherical harmonics. The radial function R(r) depends on the values of l and n and gives information about the distance of the electron from the proton. While, the spherical harmonics depends on the values of l, and and gives information about the position of an electron around the proton. Thus, the values of n, l, and are required to describe the total wave function . So, can be written as follows:
Energy of electrons in hydrogen atom
The solution of radial equation results in the quantization of energy, i.e., the energy of an electron in state of a hydrogen atom is as follows:
... (7)
Here, .
Here, the negative sign of energy represents that the electron is bound to the nucleus (or proton).
Now, it is clear from equation (7) that the energy of electron does not depend on the magnetic quantum number () and orbital angular momentum (l) while depends only on the principal quantum number (n), whose value is greater than zero.
Radial probability density of hydrogen atom
The position of an electron is not well defined. Therefore, to find the electron in a certain region of space in an atom, its probability in that region is calculated. The probability density is defined as the probability of finding an electron per unit volume in state ψ(r,θ,ϕ). According to Max Born, the absolute square of the wave function, i.e., ψ(r,θ,) gives the probability density P of finding the electron in a small volume element of volume dV centered at any point K(r,θ,ϕ).
The volume dV of the small volume element in spherical polar coordinates is as follows:
Thus, the probability of finding the electron in the volume element dV in a certain region of space is as follows
Let us assume that the electron in a hydrogen atom is in the ground state, which has the principal quantum number n = 1. Therefore, the allowed values of l and will be l=0 and =0.
Therefore, the value of wave function will depend only on the radial wave function R(r). Variation of the radial wave function for an electron present in the ground state of a hydrogen atom is plotted in the figure below.
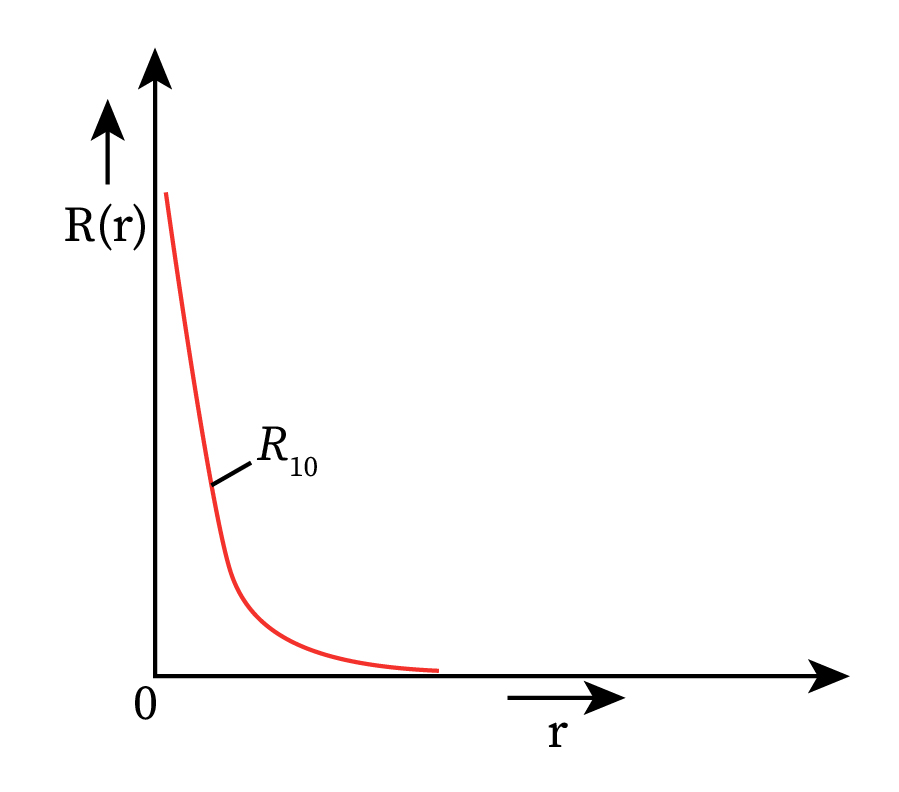
Thus, the probability of finding the electron over a distance dr will depend on the quantum numbers n and l and is given as follows:
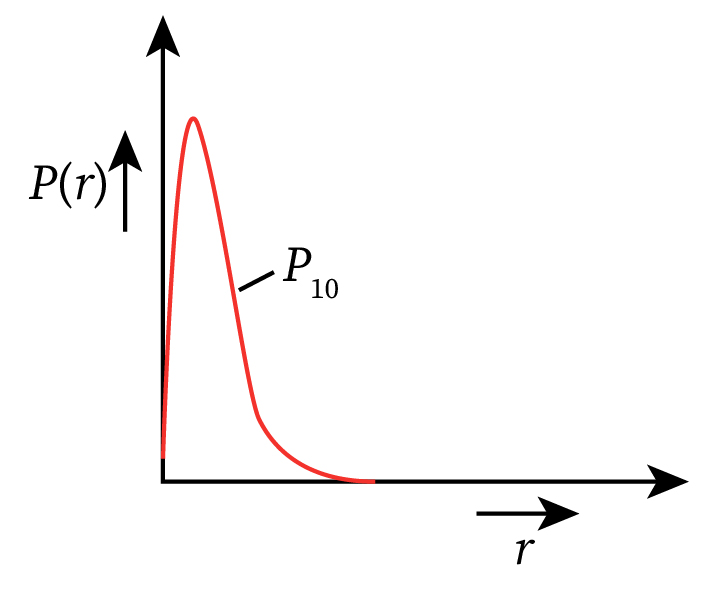
Therefore, the radial probability density P(r) is as follows:
The radial probability density function curve for the electron in the ground state of a hydrogen atom is shown below.
Common Mistakes
Students often get confused with the magnetic quantum number and orbital angular quantum number. Both the quantum numbers provide information about the electron in an atom but are entirely different.
- The magnetic quantum number divides a sublevel into orbitals, whereas the orbital angular momentum quantum number divides an energy level into sublevels.
- The magnetic quantum number gives information about the orientation of an orbital in space, whereas the orbital angular momentum quantum number gives information about the shape of an orbital.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses. Especially for
- Bachelor of Science in Physics
- Bachelor of Science in Nanotechnology
- Bachelor of Science in Material Science
- Bachelor of Technology in Electronics Engineering
- Master of Science in Applied Physics
- Master of Science in Chemistry
Related Concepts
- Radial probability density
- Angular momentum
- Potential well
- Bohr’s model of the hydrogen atom
Practice Problems
Q1: What will be the value of the angular momentum of an electron in l = 2 state?
(a)2h
(b)2h
(c)3h
(d)6h
Correct Option: (d)
Explanation: The formula to calculate the angular momentum of an electron is given by,
Q2: Which quantum number gives information about the orientation of an orbital in space?
(a) Spin quantum number
(b) Magnetic quantum number
(c) Orbital angular momentum quantum number
(d) Principal quantum number
Correct Option: (b)
Explanation: The magnetic quantum number expresses the number of orientations made by an electron. The magnetic quantum number relies on the angular momentum quantum number.
Q3: How many sublevels are there in an energy level whose principal quantum number is three?
(a) 0
(b) 1
(c) 2
(d) 3
Correct Option: (d)
Explanation: The number of sub-levels in an energy level is equivalent to the principal quantum number. So, for the principal quantum number 3, the number of sublevels is 3.
Q4: How many orbitals are there in a sublevel whose value of orbital angular momentum quantum number is l?
(a) 2l
(b) l
(c) l+1
(d) 2l+1
Correct Option: (d)
Explanation: When the orbital angular momentum quantum number is l, the number of orbitals in a sublevel can be determined by using 2l+1.
Q5: What is the energy of ground state of a hydrogen atom?
(a) -3.6 eV
(b) +13.6 eV
(c) -13.6 eV
(d) 0 eV
Correct Option: (c)
Explanation: The hydrogen atom's energy in the ground state will be -13.6 eV. It is negative because of the bounding of electrons to the H-atom.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Quantum mechanics and hydrogen atom Homework Questions from Fellow Students
Browse our recently answered Quantum mechanics and hydrogen atom homework questions.