What is Recoil Velocity?
The amount of backward thrust or force experienced by a person when he/she shoots a gun in the forward direction is called recoil velocity. This phenomenon always follows the law of conservation of linear momentum.
The Laws of Physics and Recoil velocity
When a shooter shoots a bullet (projectile) using a firearm it is bound to happen that he/she experiences a backward velocity or thrust as the projectile experiences a force by the firing of the projectile in the forward direction. This thrust acts as a compensator to the force and thus abides by the universal laws of Sir Isaac Newton. Third law of motion states that there is always an equal and opposite reaction to any action taken. This velocity is no stranger to this law.
The most important concept about this phenomenon is that the recoil impulse experienced by the firearm and the shooter goes directly to the ground. The transferring of this recoil impulse can be seen when the shooter moves backward a little after firing from his firearm.
This has many real world examples ranging from firing a projectile to shooting a basketball. In the world we live in, everything follows physics be it nature or even human biomechanics. When a basketball player shoots the ball he tends to receive a backward motion as the ball gains some forward speed. This example also shows that the third law of motion is obeyed here.
Law of conservation of momentum and energy
Whenever a body moves it gains some energy while accelerating in a certain direction.
This in turn exerts some opposite thrust or force to the moving body either by friction or by any other force in the opposite direction.
Let us consider a simple example of a car hitting a wall. The car after hitting the wall moves backward as it experiences a thrust opposite to its actual motion.
We also saw the thrust experienced by the firearm when the projectile is fired. The thing to understand is that the total momentum of the whole system consisting of the car and the wall or the firearm and the projectile remains the same as a form of force tries to compensate for another form of force in order to maintain the whole system at equilibrium. Hence, this phenomenon also follows the law of momentum conservation.
When the impulse of the body changes the system experiences a sudden change in the value of kinetic energy of the individual components of the system. The firearm and the projectile experience a change in their kinetic energies but the total energy before and after the phenomenon remains the same.
A recoilless rifle, a recoilless launcher, or recoilless gun, also abbreviated as "RR" or "RCL" is a kind of lightweight artillery system which at the moment of firing, is made to eject a propellant gas from the rear of the weapon, to counteract the weapon’s recoil. This recoilless system acts as a countermeasure to eradicate the adverse effects of recoiling on the person carrying it.
Momentum: What’s that?
Momentum in terms of physics is defined as the change in velocity of a body with mass m.
Mathematically it is shown as:
( is momentum; is mass of the body; is velocity of the body)
One of the most common real life examples of this is when a car suddenly experiences a dipping road and the speed increases due to the change in angle hence the car gains a certain momentum in that direction.
Mathematical expression for recoil velocity
Initially velocity of firearm and bullet are going to be zero.
u1 and u2 is zero.
let m and M be the mass of bullet and firearm respectively.
Hence the sum of initial energy of the gun and the bullet is zero as both of them are at rest.
If v1 and v2 are the final velocities of bullet and firearm respectively after firing.
According to the law of conservation of momentum the total momentum of the system should remain conserved.
The negative sign means that the firearm 's velocity is in the opposite direction to that of bullet's.
The negative sign is for the velocity of the pellet opposite in direction to the speed of the firearm. Thus the energy of the firearm changes but the total momentum of the system remains the same.
Recoil Energy
The value of energy after the pellet is fired and before the system is at rest remains the same for every physical occurrence in the universe.
The pellet after being fired explodes at a tremendous speed and the chemical reaction produced inside the gun produces thermodynamic energy.
This thermodynamic energy in turn produces kinetic energy which is mostly used by the pellet, due to its small proportion.
Let the initial Energy of the fired pellet be Eb and the Energy of the gun after be Ef.
Now,
----------1
and
-----------2
From the principle of conservation of energy,
-----------3
Using equations 1 and 2 in 3 we get:
∴This ratio is used for calculating the recoil energy by just knowing the ratio of their respective masses.
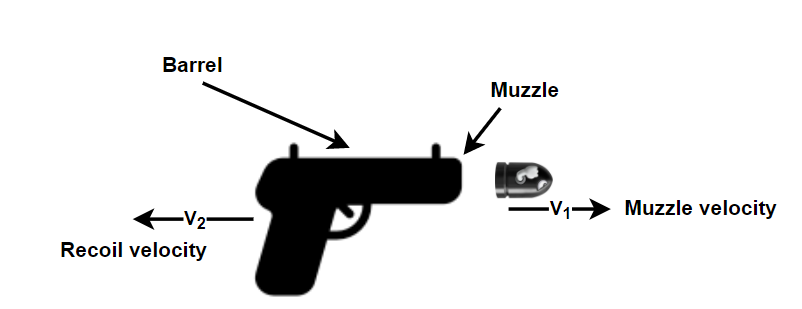
Muzzle velocity and its effects on recoil
Muzzle is the protruding segment of a carbine (a firearm with longer barrel), which provides an opening pathway for the bullet. Muzzle velocity determines the speed of the pellet as it just leaves the gun’s muzzle. Muzzle velocity sometimes is determined by the quantity and quality of the propellant, the pellet’s weight and length of the system. Propellant needs a longer path to finish its burn before leaving, if it is a slow burning one, but heavier shells can be used by it. For the same quantity of propellant, a fat burning one can lead to higher acceleration of a lighter shell. Evidently, the quality and the amount of propellant as well as the length of barrel must all be compensated evenly to balance the system and achieve safety and optimal performance.
Recoil can be expressed in two forms: physical and felt. Physical is the amount of strength generated by the gunshot itself and felt is how that force is experienced by the person shooting the gun. Speed affects recoil, as we know from F=MA, but quantity is the more prominent one of the two. Greater the bulk of the gun, less the recoil force being transmitted into the shooter.
Consider the following example, to understand the effect of muzzle velocity.
Q. Let the mass of the gun and pellet be 2 kg and 10 g respectively, the muzzle velocity being 300 m/s, calculate R.V.
A. By conservation of momentum we have, , where are the initial velocities of gun which are both 0 and pellet respectively and are the final velocities.
Applying given values we get
comes to be
Common Mistakes
The most common mistake or pitfall that physics students make is that they believe theoretically about the real life incidents taking place. Let us take an example of a bullet hitting a target at a distance.
The target is assumed to fall some metres away after the bullet is hit which is also a common thing shown in action movies.
This phenomenon is not true practically as the kinetic energy imparted to the bullet does not get transferred to the target fully.
Only a fraction of the energy is transferred and most of the energy is used in fragmenting the bullet inside the target.
The energy transferred to the bullet and to the target theoretically should be significant but when seen in reality the answer turns out to be different as seen from the equation derived earlier:
Context and Applications
The whole idea of recoil speed is based on the law of conservation of momentum.
This law is used in many situations based on the need.
- Rocket propulsion systems
- Used by skaters, spinners
- In Rocket propulsion systems the rocket moves in space by abiding by this law.
- Spinners and skaters rotate their body changing their COM and thus the moment of inertia which helps them in conserving their energy while spinning.
This topic is very crucial for undergraduate as well as higher degrees in various technical fields like:
- Bachelors in Science Physics(Hons.)
- Masters in Science Physics(Hons.)
- Bachelors in Technology (Civil, Mechanical, Electrical)
- Masters in Technology (Civil, Mechanical, Electrical)
Related Concepts
- Impulse
- Energy conservation
- Change in acceleration
Practice Problem
Q. Calculate the recoil velocity of a carbine whose mass is 10 kilograms and it shoots a bullet weighing 0.500 grams. The velocity of the shell is 600 m/s.
A. Given-
mass of carbine M =10 kg
mass of shell m =0.5 kg
velocity of shell v1 = 600 m/s
R = =
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Recoil Velocity Homework Questions from Fellow Students
Browse our recently answered Recoil Velocity homework questions.