What are Relativistic Energy and Momentum?
The concept of relativistic energy and relativistic momentum is a prominent topic in modern physics. The relativistic energy-momentum is the prominent outcome of the special theory of relativity. It also gives very important relations, the relation is one of its outcomes.
According to classical physics, time flow is the same for every observer. But according to einstein's theory, time flow is different for different observers. The idea that time flow is not the same for all may sound strange because we may not experience this effect in everyday life. This effect is only observed when an object moves with some velocity comparable to the velocity of light. This velocity is termed relativistic velocity.
Introduction to the special theory of relativity
Einstein’s special relativity was developed based on two postulates:
- The laws of physics are the same for all inertial frames of reference.
- The velocity of light in a vacuum is the same for all observers, irrespective of the velocity of the light source.
Suppose a truck is moving with a velocity of 50 km/h if a person throws an object from the truck along the traveling direction with a velocity of 0.5 km/h. For an observer standing still on road, the object travels at 50.5 km/h. The speed of the thrown object depends upon the speed of its source; but, the light particles do not behave in this manner. Suppose a beam of torchlight is shone from the truck; whereas the velocity of photons remains the same it does not matter where the observer is or how fast the observer is moving. However, the velocity of the photon remains the same.
The classical physicist thought that the velocity of light is not constant. But the predictions of relativity disagree with the classical physicists. Hence, the Galilean transformation that is applied in classical mechanics cannot be used in modern physics. A special type of transformation called the Lorentz transformation rule is used to transform from one frame to another.
Consider two frames with co-ordinates (x,y,z) and (x',y',z'). If the non-dashed frame was at rest whereas the dashed frame is moving in along a line at a certain velocity v along x-direction with respect to the non-dashed frame of reference.
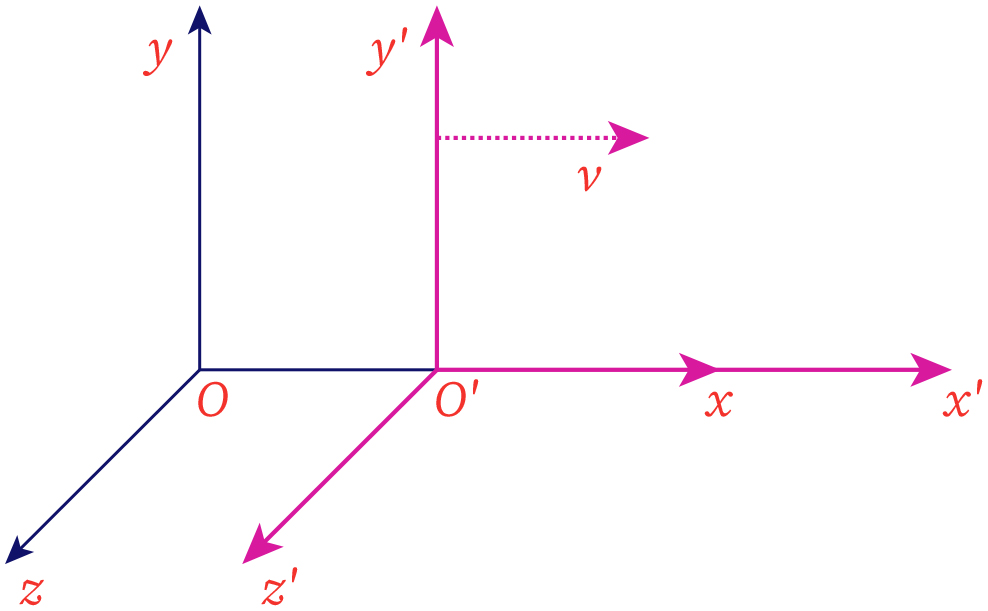
Lorentz transformation rules are,
The coordinates y and z are invariant under the lorentz transform since there is no motion along with these directions.
Where,
Outcome of special relativity-relativistic mass and energy
When any object travels at relativistic speed, the following relativistic effects are observed.
- Length contraction: Any object of a certain length moves along the length of an object with a velocity close to the velocity of light, the apparent length measured from the rest frame of reference will be shorter than the length measured at rest.
- Time dilation: The time is not absolute which means time is different for different observers. If two clocks shows the same time initially suppose one of the clocks travels at relativistic speed, the time of moving clock/object dilates; hence, the moving clocks stay behind the time.
- Mass variance: Any object will have two kinds of mass, the rest mass and relativistic mass. When the object is not moving the mass of that object is known as rest mass. Suppose the object moves with some velocity the apparent mass changes this mass is called the relativistic mass. This is the same as rest mass, if the speed is much less compared to the velocity of light.
The relativistic mass of the object increases with velocity because the kinetic energy of the moving body increases. The very prominent result of relativity is that mass and energy are inter-convertible. This concept is the fundamental principle of nuclear energy.
The rest mass and the relativistic mass m can be related by following the equation using special relativity.
or
where
Hence, for a relativistic motion, the relativistic momentum is the product of the relativistic mass of moving object and velocity.
i.e.
Similarly, from relativity the kinetic energy is,
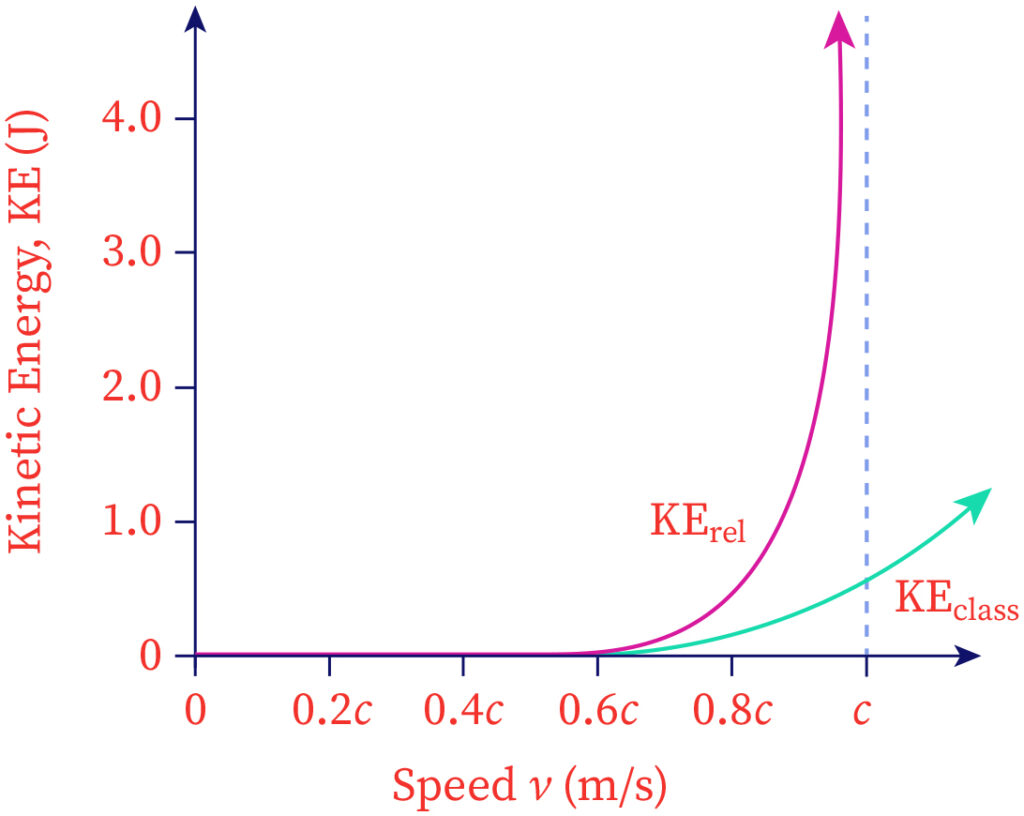
The following graph shows the change in the relativistic kinetic energy and classical kinetic energy as velocity changes.
Energy-Momentum relation
The relation between the energy and the momentum for a relativistic case can be arrived at by using newtons law as,
m0 is the rest mass.
E is the total energy.
When velocity is zero then the momentum p=0; hence, the equation for total energy becomes,
This equation gives the relation between rest energy and the rest mass.
Thus, special relativity predicts that objects possess rest energy even the object is not moving at all. This equation also predicts that the rest energy can be transformed to mass and mass can transform to energy.
In nuclear reactions, the bulk atoms break down into smaller atoms and release a huge quantity of energy. If the net mass of reactants and the total mass of products are compared, it is observed that some fraction of mass will disappear this mass gets converted to energy. The energy released will be equal to the product of mass and the velocity of light squared. When a fraction of mass gets disappeared, the mass gets converted to another form of energy like kinetic energy, electromagnetic energy, or heat energy. Even though some energy is lost the law of conservation of energy is not violated the energy is stored within the system as mass hence the total energy remains constant. Suppose the particles like photons that do not at all have mass can still have kinetic energy because they possess momentum. The kinetic energy of the massless particles is expressed in terms of momentum using,
Hence, the total energy of the photon is,
or
Where,
h is the plank’s constant.
ν is the frequency of photon.
Formulas
The relativistic mass m from special relativity can be expressed from rest mass using the following equation,
Where,
v is the velocity.
c is the velocity of light.
The relativistic momentum is,
Where, is the rest mass.
The relation between total energy and relativistic momentum can be given as,
p is the momentum.
The relativistic kinetic energy is,
If the object is not moving then, kinetic energy becomes zero hence, total energy becomes the rest energy,
This energy is called rest energy.
If the mass is zero then the total energy of the massless particle is,
(in joules)
Where h is the plank’s constant.
ν is the frequency.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for bachelors and masters in science (physics).
Practice Problems
Question 1: What is the relativistic kinetic energy of the electron? If velocity of the fast-moving electron is 0.87c. Given .
(a) 0.767 MeV (b) 0.699 MeV
(c) 0.527 MeV (d) 0.356 MeV
Answer: The correct option is c.
Given data:
Velocity v=0.87c
Rest mass
Kinetic energy ?
Explanation:
To find the rest energy:
is the rest energy of the electron
To find kinetic energy of the electron,
Kinetic energy is,
The kinetic energy of the electron is 0.527 MeV.
Question 2: According to relativity, an object at rest possesses the internal energy called ____.
(a) Nuclear energy (b) Rest energy
(c) Potential energy (d) Chemical energy
Answer: The correct option is b.
Explanation: Special theory of relativity predicts that the object at rest posses enery called rest energy which is equal to the product of the mass and the square of the velocity of light.
Question 3: Which of the following is not the outcome of special relativity?
(a) Mass variance
(b) Time dilation
(c) Conservation of energy
(d) Length contraction
Answer: The correct option is c.
Explanation: The special theory of relativity says that speed of light is constant thus the effects like mass variance, time dilation and length contraction are obtained from relativity. It is clear that conservation of energy is not the outcome of special relativity.
Question 4: When an object travel close to speed of light, the length observed from the rest frame is ___ the original length.
(a) Smaller than
(b)Larger than
(c) Same as
(d) None of the above
Answer: The correct option is a.
Explanation: Any object travelling at relativistic speed undergoes the length contraction effect. When the length is observed from a rest frame the observed length will be smaller than the initial length. Thus, option (a) is the correct answer.
Question 5: The relativistic kinetic energy of any object does not depends upon _____.
(a) Rest mass (b) Velocity
(c) Acceleration (d) Momentum
Answer: The correct option is c.
Explanation: The relativistic kinetic energy depends upon the rest mass and the velocity of the object. Also the momentum is related to the kinetic energy. But the relativity is true only for the inertial frame hence the acceleration is not related to the relativistic kinetic energy.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Relativistic Energy and Momentum Homework Questions from Fellow Students
Browse our recently answered Relativistic Energy and Momentum homework questions.