What is resistivity?
Resistivity is a characteristic property of the conductor’s material that measures the extent to which the material opposes the flow of current. It is denoted by the Greek letter “rho”. Electrical resistivity, also known as specific resistance, depends on the nature of the material of the conductor and is unaffected by its dimensions.
What is the formula for resistivity?
Consider a conductor made of a single material, having length l, uniform area of cross-section A, and resistance R. This is shown in the figure below:

If the flow of current is uniform throughout the conductor, then the resistivity of the conductor’s material can be measured using the following formula:
... (1)
Definition of resistivity in terms of resistance
If the length of the conductor is l =1 m and the area of cross-section is A =1 , then using equation (1), we get:
... (2)
Therefore, resistivity can also be explained as the resistance provided by a unit length and unit cross-sectional area of the material.
Electrical resistivity can also be referred to as the resistance offered by a unit cube of the material of a conductor.
SI unit of resistivity
On substituting SI units of l (m), A and R (ohm) in equation (1), we get:
Thus, SI unit of resistivity is .
What are the factors that affect the resistivity of a material?
Consider a uniform conducting wire of length l, area of cross-section A, and resistance R. When a voltage V is applied across the ends of the conductor with the help of a battery, current I starts flowing through it. This is shown in the figure below:
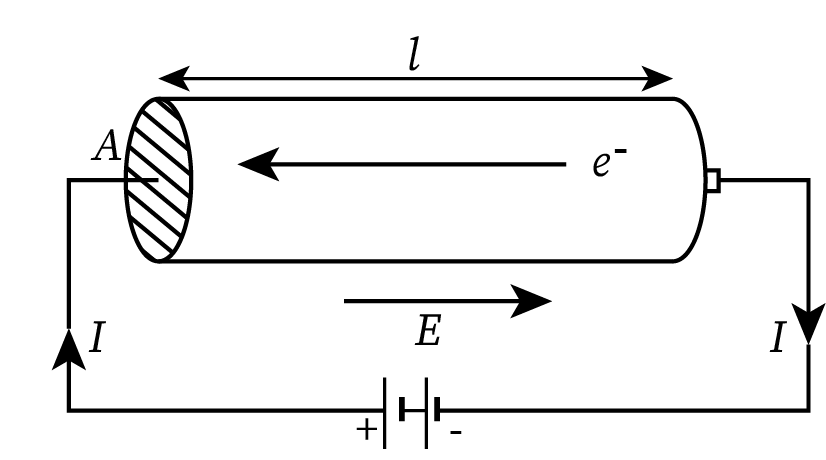
As per Ohm’s law, the voltage across the ends of the conductor can be written as:
... (3)
The electric field generated across the conductor is:
... (4)
Current I flowing through the conductor is given as:
... (5)
Here, n is the number density of electrons, e is the charge on an electron, m is the mass of an electron, and τ is the average relaxation time of the free electrons in the conductor.
On substituting equations (5) in (3), the resistance of the conductor can be written as:
... (6)
Also, we know that the resistivity of the material of a conductor is given as:
... (7)
On substituting equation (6) in (7), the resistivity of the material of a conductor can be written as:
... (8)
Since the charge on the electron and its mass are constant, it is clear from relation (6) that the resistivity of a material depends on the following factors:
- Nature of the conductor material.
- The temperature of the conductor.
Nature of the material of the conductor
According to relation (6), the resistivity of a conductor’s material is inversely proportional to the number density of the electrons. Inside the conductor, the number of electrons depends on the nature of the material. Therefore, we may conclude that the electrical resistivity of a material is determined by the nature of the conductor’s material.
The values of resistivity of different materials are shown in the table below:
| Type of Material | Material | Resistivity Ω m |
| CONDUCTORS (Metals) | Silver | 1.6×10-8 |
| Copper | 1.7×10-8 | |
| Aluminium | 2.7×10-8 | |
| Tungsten | 5.6×10-8 | |
| Iron | 10×10-8 | |
| CONDUCTORS (Alloys) | Nichrome | 100×10-8 |
| Manganin | 44×10-8 | |
| Constantan | 49×10-8 | |
| SEMICONDUCTORS | Germanium | 0.46 |
| Silicon | 0.1-60 | |
| INSULATORS | Glass | 1010‐1014 |
| Wool | 108‐1011 | |
| Rubber | 1013‐1016 |
It can be clearly seen from the above table that conductors have very low values of electric resistivity (of the order of) and insulators have a very high value of resistivity (of the order of and greater). Moreover, the values of the resistivity of semiconductors lie within the range of the values of resistivity of conductors and insulators.
Also, it can be seen that the resistivity of alloys is very high, implying that producing wires of the given resistance and the given diameter from alloys will require small lengths.
The temperature of the conductor
It is clear from relation (8) that the resistivity of the material of a conductor ρ is inversely proportional to the average relaxation time τ of the free electrons moving in the conductor.
The value of relaxation time changes with a change in the conductor’s temperature. Thus, we can state that the resistivity of a conductor’s material depends upon its temperature.
How do the resistivities of different materials vary with temperature?
Materials are classified into three types, i.e., conductors, insulators, and semiconductors, based on their electrical resistivity. The variation in the resistivity of a material with temperature depends upon the type of material. On changing the temperature, resistivity varies differently for different types of materials. Let us discuss the variation in resistivity for each type of material in detail.
For conductors
Metallic conductors
On increasing the temperature of a metallic conductor, the thermal speed of the free electrons moving from one end of the conductor to the other increases, but the number density (n) of free electrons does not change by a considerable amount. Also, the atoms or ions in the metal start to vibrate around their mean position with higher amplitudes and frequencies. As a result, the probability of the electrons colliding with the atoms increases. Hence free electrons collide more frequently with the atoms or ions. Therefore, the average relaxation time τ of the free electrons decreases.
It is important to remember that the resistivity of a material is inversely proportional to the number density of free electrons (n) and their average relaxation time τ. Therefore, the resistivity of metallic conductors increases with an increase in temperature.
If is the initial resistivity of a metallic conductor at temperature , then resistivity ρ of the metallic conductor, when the temperature has increased to T, is given by the following relation:
The above relation shows the temperature dependency of a metallic conductor’s resistivity. This relation can also be written as:
... (9)
Here, α is known as the temperature coefficient of resistivity and is defined as the increase in resistivity per unit of original resistivity with per degree of temperature increase.
The value of α will be positive for metals as the resistivity of metals increases with the increase in temperature. The variation in resistivity of a particular metal with temperature is shown graphically in the figure below:
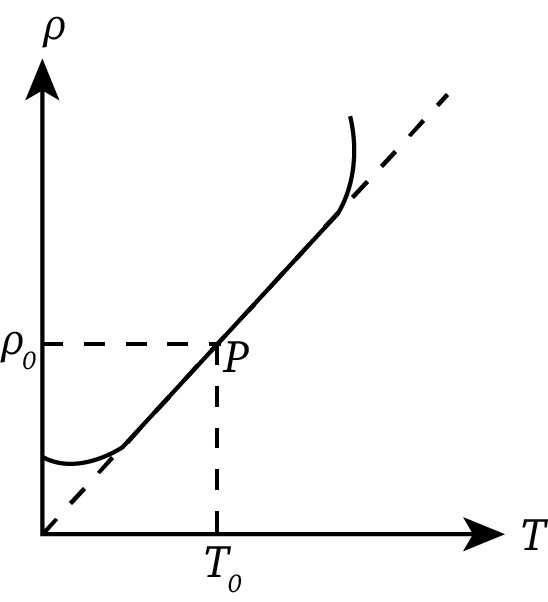
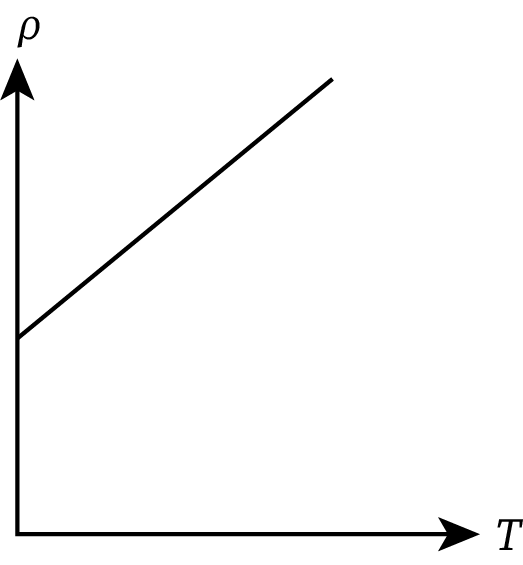
For alloys
The resistivity of alloys like Constantan, Nichrome, and Manganin varies by a little with a rise in temperature. This happens because the resistivity of alloys does not depend much on temperature. The fluctuation of an alloy’s resistivity with temperature is shown graphically in the figure below:
For semiconductors
As the temperature of a semiconductor rises, the average relaxation time τ reduces, while the number density of free electrons (n) increases. However, the increase in the number of free electrons’ density is much more than the reduction in relaxation time.
Since the resistivity of a material is inversely proportional to the number density of free electrons (n) and average relaxation time τ, the resistivity of semiconductors declines as temperature rises.
It is clear from relation (9) that the value of α will be negative for semiconductors as the resistivity of semiconductors falls with an increase in temperature. The variation in the resistivity of a semiconductor with temperature is graphically depicted in the figure below:
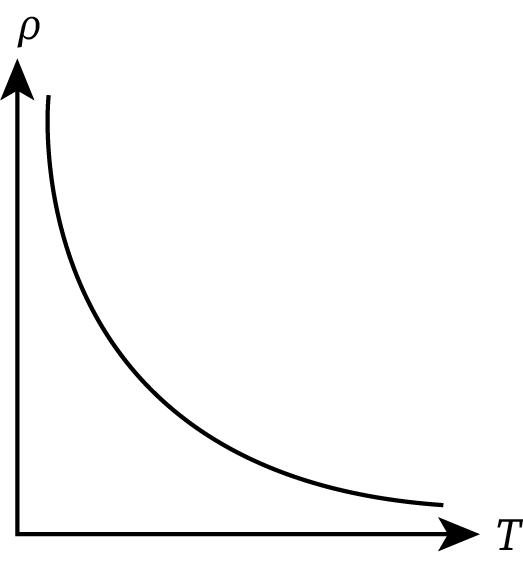
For Insulators
An insulator's resistance falls exponentially as its temperature rises. The conductivity of insulators drops to almost zero at absolute zero temperature. Therefore, the resistivity of insulators is infinitely large at absolute zero temperature. Thus, the value of α is negative for insulators.
Formulas
- The resistivity of any material is given as , where R is the resistance, A is the cross-sectional area, and l is the length of the conducting material.
- The conductivity σ of a conductor is the reciprocal of its electrical resistivity and is written as .
- The resistivity ρ of any conducting wire in terms of relaxation time τ, electronic charge e, electron density n, and the mass of electron m is given by .
- The temperature coefficient of resistivity is given as , where is the initial resistivity of a metallic conductor at temperature and is the resistivity of the metallic conductor when the temperature increases to T.
Common Mistakes
When measuring the resistivity of conductive materials like metals, the potential error sources are usually external noise sources or voltmeters with insufficient sensitivity. To eliminate such errors, the four-wire method should be used where a set of two leads is used to source the current, and another set is used to measure the voltage drop across the conductor.
Context and Applications
This topic is significant to various professional exams for undergraduate courses such as:
- Bachelor of Engineering in Electrical Engineering
- Bachelor of Engineering in Civil Engineering
- Bachelor of Engineering in Mechanical Engineering
- Bachelor of Science in Physics
- Master of Science in Applied Physics
Related Concepts
- Electric current
- Electric resistance
- Conductance
- Superconductivity
Practice Problems
Q1. On increasing the temperature of a metallic conductor, its resistivity:
a. Increases
b. Decreases
c. Remains the same
d. Does not change
Correct option: (a)
Explanation: The resistivity of the conductor is directly proportional to the temperature of the conductor. Hence, on increasing or decreasing the temperature of the conductor, its resistivity will also increase or decrease respectively.
Q2. The value of the temperature coefficient of resistivity is negative for:
a. Copper
b. Tungsten
c. Aluminum
d. Silicon
Correct option: (d)
Explanation: The negative temperature coefficient of resistivity indicates that the resistance of the material decreases with temperature increase. Generally, negative temperature coefficient of resistivity exists in semiconducting materials like carbon, silicon, germanium etc.
Q3. Out of the following materials, whose resistivity increases with an increase in temperature?
a. Germanium
b. Silicon
c. Tungsten
d. Wood
Correct option: (c)
Explanation: If the material's resistivity increases with temperature increase, it means the material is a pure conductor. Wood is an insulator, and silicon and germanium are semiconducting materials that have a negative temperature coefficient of resistivity.
Q4. What is the resistivity of the material of a wire that is 1 m long, 0.5 mm in diameter, and has a resistance of 2.5 ohm?
Correct option: (b)
Explanation: The resistivity of the material is as follows:
Q5. The resistivity of material of a wire is . What will be its new resistivity if length of the wire is doubled? (Assume resistance and area remains unchanged).
Correct option: (d)
Explanation: The resistivity is described as a characteristic feature of the material that gives an idea about the flowability of electricity in the material. It only varies with the temperature of the material and is independent of the length of the conductor or material.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Resistivity Homework Questions from Fellow Students
Browse our recently answered Resistivity homework questions.