What is a rigid body?
A rigid body is an object which does not change its shape or undergo any significant deformation due to an external force or movement. Mathematically speaking, the distance between any two points inside the body doesn't change in any situation.
Mechanics of rigid body
While analyzing the rigid body in different situations, we use the mathematical property of the rigid body to analyze most of the situations. The three states of motion of the rigid body are:
- Equilibrium
- Translational motion
- Rotational motion
Equilibrium
When a rigid body is in equilibrium, its velocity vector remains unchanged. It does not undergo any linear or rotational acceleration. When multiple forces are acting on it and it stays in equilibrium, then, the vector sum of all the forces and moments about any point is always zero.
Consider a rigid body ‘A’ stays in equilibrium being acted upon by different forces at different positions on the body. An i'th force is generally shown at a point P from the chosen axis of reference.
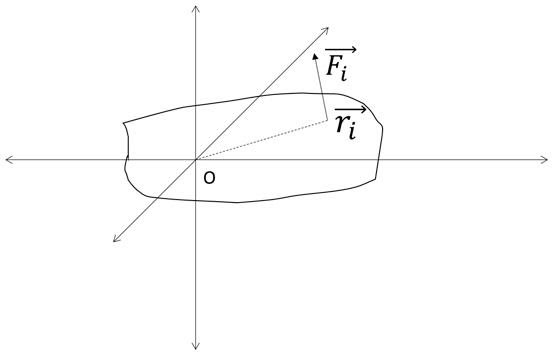
The sum of all the forces acting on the body is given by,
Sum of all forces =
The sum of the moments of all the forces about the point O is given by,
Sum of all the moments =
Applying the condition of equilibrium, we get, =0 and =0
Translational Motion
A rigid body is said to be in translational motion when all points in the moving body move uniformly in the same direction or line.
The moving points do not change their orientation as a result,
- they don't vibrate
- they don't rotate
In this case, all the points inside the body have the same velocity and acceleration.
For example, a rocket fired from the launch station has all its points moving at the same speed. The velocity and acceleration of all the particles at any point in time are obtained by using Newton's laws and Kinematic equations.
Newton's second law of motion states that the resultant external force is related to acceleration as,
Here, 'a' is the acceleration of the body and M is its mass. The left-hand side is the vector sum of all the external forces acting on the body.
In a pure translational motion, the resultant of the forces might be non-zero, but the sum of moments of all the forces must be zero.
Rotational Motion
A body is said to be in rotational motion when all the particles move in a circular path around a point, which is called the point of rotation. The angle made by the line joining the point of rotation (O) and a random point (P) with a given reference axis changes with time. In other words, the angular position of the point changes with time as demonstrated by the figure below. In the figure, θ is the initial angular position of the point and P is its initial position for the given reference axes. P' is the final position and θ' is the final angular position of the point.
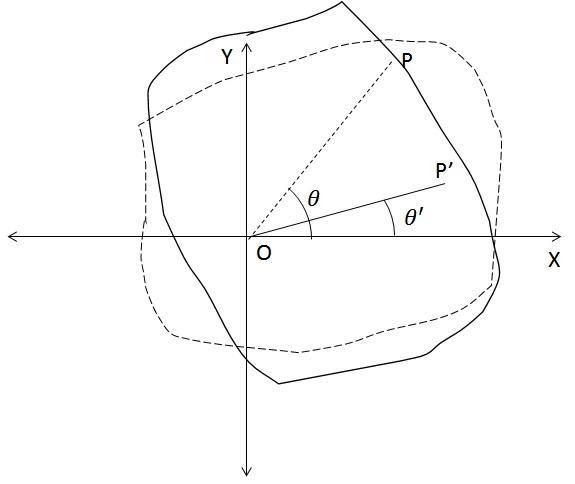
The change in angle within the time period is given by,
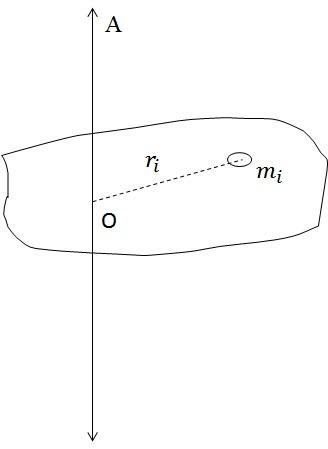
The rate of change of angular position is analogous to the velocity in translation motion and is termed angular velocity. Similarly, there is angular acceleration. The rotation of the rigid body happens around an imaginary line called the axis of rotation. The axis of rotation is perpendicular to the plane of rotation of the body. Now, the object in the figure is rotating in the X-Y plane, the axis of rotation would be passing through O and perpendicular to the X-Y plane. Similar to translation, we can use Newton's laws and kinematic equations to determine the angular position, velocity, and acceleration at any given time. In the place of force in translational motion, here, we use the moment or torque of the force about the axis of rotation. A quantity called the moment of inertia replaces mass. The moment of inertia of a rigid body about an axis of rotation is given by,
Moment of inertia
Here, is the mass of the element of the body and is the perpendicular distance of the element from the axis of rotation as shown in the figure.
Now, the second law of motion in rotational mechanics becomes,
Here, is the angular acceleration and the right-hand side is the sum of moments of all the forces or the resultant torque acting on the rigid body. For a single force F at a distance r from the given axis, its torque about the axis is given by,
Torque
=
Torque is analogous to force in rotational motion.
A rigid body may undergo a combination of these motions. But the condition of non-deformation holds no matter what. The distance between any two points remains constant. This can also be said in other terms that the relative velocity along the line joining any two points is zero. If we take a rigid rod of length L in motion, If two points A and B have different velocities as shown in the figure, the relative velocity of the point along the line joining (or the length of the rod in this case) is zero.
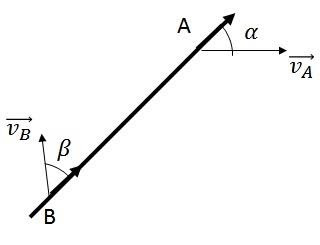
In the above figure, if we calculate the components of the velocities of points A and B along the rod and apply the condition, we get,
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Technology (Mechanical Engineering)
- Masters in Technology (Mechanical Engineering)
- Bachelors in Science in Physics
Practice Problems
Q 1. When a rigid body is in translational motion, all the particles inside the body has
- Same velocity
- Same acceleration
- Different speed
- Both (a) and (b)
Answer: (d)- Both (a) and (b)
Explanation- When a rigid body is in translational motion, all the particles inside the body have the same velocity and acceleration.
Q 2. The vector cross product of force and distance of the position of the force gives,
- Torque of the force
- Angular acceleration of force
- Angular velocity of force
- The angular position of force
Answer: (a) Torque of the force
Explanation- The vector cross product of force and distance of the position of the force gives the torque or the moment of force.
Q 3. Which of the following Newton's law of motion states that the force is proportional to acceleration?
- Newton's I law of motion
- Newton's II law of motion
- Faraday law of motion
- Newton's III law motion
Answer: (b) Newton's II law of motion
Explanation- Newton's II law states that the acceleration of a body is proportional to force.
Q 4. What is the sum of torques in a pure translational motion?
- Zero
- Less than zero
- Greater than zero
- Can't say
Answer: (a) - Zero
Explanation- In a pure translation, the sum of torques is always zero.
Q 5. Which of the following is/are characteristic/s of a rigid body?
- Rotatable
- Inextensible and non-deformable
- Movable
- Bendable
Answer: (b)-Inextensible and non-deformable
Explanation- A rigid body is inextensible and non-deformable.
Formulas
If a rigid body is in equilibrium, then
- Newton's second law in translational motion is given by,
=
- The moment of inertia of a body is given by,
=
- Newton's second law in rotational motion is given by,
=
Related Concepts
- Newton's laws
- Mechanics
- Rotational motion
- Kinematics
- Centre of mass
- Moment of inertia
- Angular motion
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Rigid Body Homework Questions from Fellow Students
Browse our recently answered Rigid Body homework questions.