What is Rigid Body Dynamics?
Rigid bodies are defined as inelastic shapes with negligible deformation, giving them an unchanging center of mass. It is also generally assumed that the mass of a rigid body is uniformly distributed. This property of rigid bodies comes in handy when we deal with concepts like momentum, angular momentum, force and torque. The study of these properties – viz., force, torque, momentum, and angular momentum – of a rigid body, is collectively known as rigid body dynamics (RBD).
In the ladder of increasing complexity, RBD is a logical and natural successor to point particles. Owing to their lack of spatial expanse, point particles are ideal systems for studying action of linear forces in two and three dimensions. Graduating up to rigid bodies, we add two critical components to the equation: rotational forces, and constraints. The ability to describe both linear and rotational components of motion in RBD allow us to reliably understand the wide variety of motions in many engineering systems.
Kinetics and Kinematics
RBD has two major branches: Kinetics and Kinematics. Kinetics is the study of movement of masses and the forces that act on them. Within kinetics, we deal with linear and rotational movement of free-falling objects and that of constrained objects. Since linear movement is adequately described by the basic laws of motion, the focus in RBD is mainly on the rotational component. To describe the rotational components as well as to draw equivalences and relationship with their respective linear measures, we describe measures like angular displacement, angular velocity, angular momentum, and torque [Table 1 for equivalence].
| Linear | Rotational |
| Velocity | Angular Velocity |
| Momentum | Angular Momentum |
| Force | Torque |
| Mass | Moment of Inertia |
The idea of moment is one of the key components of understanding and describing rotational motion. A moment is described as the product of the quantity of interest and the distance from the axis of rotation raised to an appropriate power. For instance, the equivalent of momentum in rotating bodies is angular momentum. Similarly, torque is the first moment of force applied to a body turning about an axis. The moment of Inertia, a product of angular velocity and angular momentum [both first order moments] is related to mass as the square of distance from the axis. It should be noted that angular momentum in a system is conserved, just as its linear counterpart. These equivalences allow us to identify and quantify forces acting on a rotating rigid body, and to understand the effect of these forces on the body. In many cases however, we are interested in the locus of positional changes and orientations, given that sufficient force has been applied. For those needs, we turn to Kinematics.
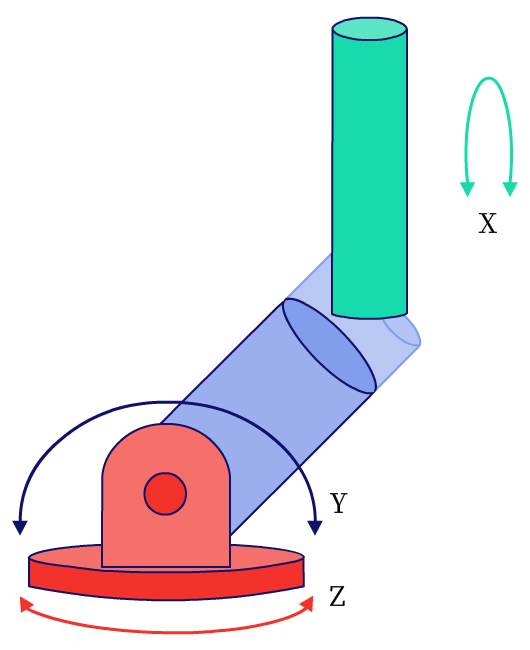
Kinematics deals with the changes in orientation of a body in n-dimensional space, without going into the details of the forces at play. It is best explained with an example of a robotic arm with a hinge and a “wrist” [see figure]. When placed on a rotating base, the robotic arm can move in the Z-axis (Yaw), Y-axis (Pitch) and X-axis (Roll). The core focus of kinematics is then the transformation of bodies by moving them through 3D space and reorienting them. The corollary is also true: the theory of kinematics allows us to match objects even if their orientation has changed. Given that the position of an object is defined by its position in 3D space, we reduce the problem of reorienting an object to one of finding the correct destination angles.
Eulerian Representation
Euler proposed that any change in orientation of a rigid body can be achieved by successively turning the body in 3D space about the principal axes. Hence, the use of individual angles to achieve a desired orientation of an object is often referred to as the Eulerian representation. One thing to note about the Eulerian representation is that the first and third rotations happen about the same principal axis. In contrast, a related system called the Tait-Bryan representation uses all three axes to orient the body. In the Tait-Bryan representation, the pitch angle (about the Y-axis) is conventionally restricted between 0 and Pi radians (0 and 180 Degrees). While these are convenient to represent the orientation of any rigid body, they are computationally costly.
Quaternion Representation
An alternative representation of orientation is the quaternion, a set of four parameters. Assuming a body at origin [0,0,0] is translated to [x,y,z] with an angle θ, then the quaternion, written as [WXYZ], is given by [ Cos[A], x * Sin[A], y*Sin[A] , z*Sin[A] ], where A = θ/2.
As can be seen, the quaternion calculation is numerically and computationally much simpler than the Eulerian translation. This way of translating and orienting rigid bodies is extensively used in programming (games) and computer aided design.
What is a Multibody Dynamic System (MBD)?
A multibody dynamic (MBD) system is one that consists of rigid or flexible solid bodies, or links, that are interconnected by joints that restrict their relative motion. Forward dynamics analyzes the movement of these mechanical systems when forces act on the system. Inverse dynamics, as the name suggests, analyzes what forces are required to make the mechanical system move or act in a specific or defined manner.
Most of the time, when solving rigid body problems, we work with forward dynamics because we already know the forces which can be used to calculate the acceleration. The time step is the time duration for which the equations are being used.
Context and Applications
Simple rigid body equations in Kinetics, and the systems of translation in Kinematics are critical in understanding complex systems. A complex system can be reliably modeled as a set of rigid bodies with spatial and rotational constraints. Such a formulation allows one to realistically understand the effect of forces on its shape, location and orientation.
Some common complex rigid body problems that can be solved using this approach include dual pendulums, the behavior of linked chains, and wheel assemblies in automobiles. This is mainly studied by students of
- Bachelors in Science ( Physics)
- Masters in Science (Physics)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Rigid Body Dynamics Homework Questions from Fellow Students
Browse our recently answered Rigid Body Dynamics homework questions.