What is Rotational Equilibrium?
In physics, the state of balance between the forces and the dynamics of motion is called the equilibrium state. The balance between various forces acting on a system in a rotational motion is called rotational equilibrium or rotational dynamics.
Rotational Dynamics
Just like linear motion has its dynamics, rotational motion has analogous dynamics. They are explained below
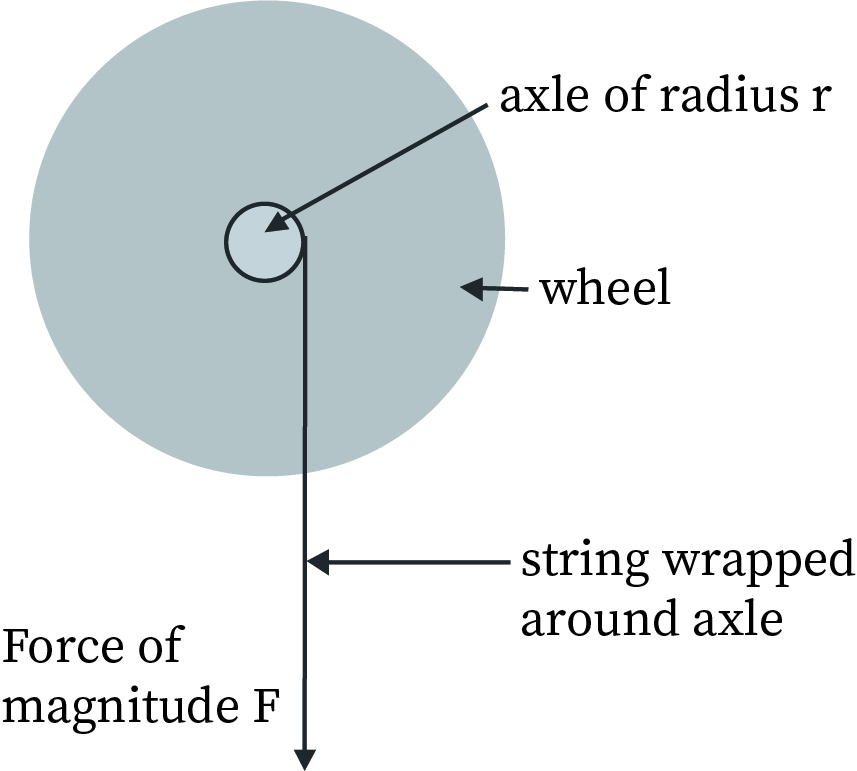
Torque is a tangential force experienced by an object in a rotational motion. The torque increases as the force and distance increase. It can also be defined as the product of force and the moment arm length which is a perpendicular distance between the rotation center of the force.
The equation of the torque is. The SI unit of torque is Newton meter.
Angular velocity is a term defined for a body when it is in a rotational motion at a constant motion at a particular speed as the rate of change of the angle of its motion. It is denoted as. The relation between angular velocity and linear velocity is where r is the radius of curvature. As per the sign convention, the counterclockwise direction is positive, and the clockwise direction is negative.
The angular acceleration is the change in angular velocity or it can be said it is the rate of
change of angular velocity. It is denoted as. The SI unit of angular acceleration is
radian per second square. If there is an increase in angular velocity, then the angular acceleration will also increase, if there is any decrease in angular velocity, then the angular acceleration will also decrease.
The moment of inertia is defined in a rotation motion. The center of mass of an object is the point where the entire mass is concentrated and when this object is in rotation motion, the equivalent mass is the moment of inertia. It is mathematically represented as the product of the sum of the masses of the particles in an object and the square of the
perpendicular distance from the axis of rotation..
Angular momentum is a term used for an object moving in a rotational motion and its momentum equals the product of the moment of inertia and the angular velocity.
mathematically represented by and it can also be defined as the moment of linear
momentum vector in the rotational motion as
In rotational dynamics concept, the angular momentum quantum number is defined as the azimuthal quantum number when the number of atomic orbital that predicts the angular momentum of an object moving in a rotational motion tells its size and shape of the orbital
Fleming's right-hand thumb rule is used for the sign conventions where if you point only your thumb and curl your other fingers, that is the direction of r. The thumb directly tells the direction of the angular momentum
Rotational Motion on a Fixed Axis of Rotation
Let's say if an object is rotating, that has zero velocity during its motion, the point on that object or away from the object determines its vectors. The axis is fixed and only the components of the torques applied to the object which is along the axis will be considered as the parameters used for calculating its rotational dynamics. The perpendicular component of the torque tends to move the axis of rotation from its position of the object. The various forces that act on the body tend to neutralize the effect of the perpendicular components, since the perpendicular components do not affect the body, they are not used for calculation in rotational dynamics. The movement of the object is restricted when it's at a fixed axis of rotation. For example, the to and fro rotation when we open or close the door, the door's axis is fixed and has only that movement.
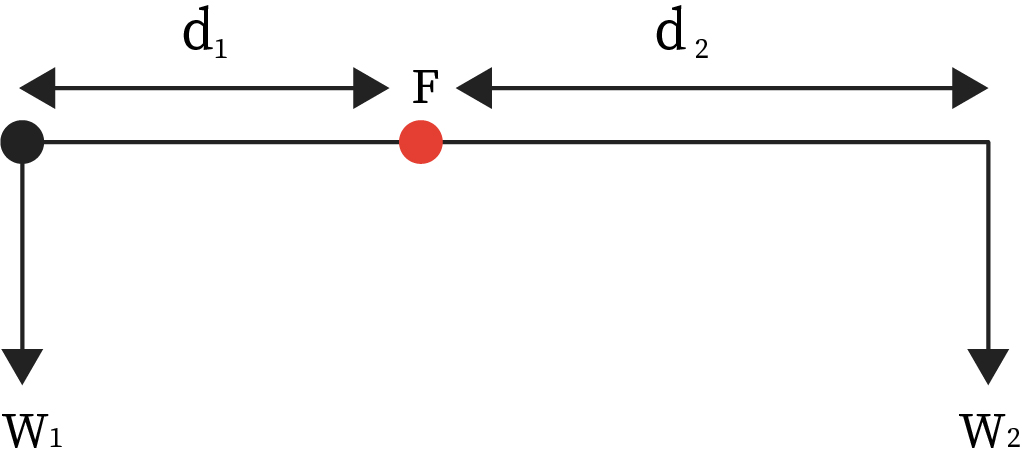
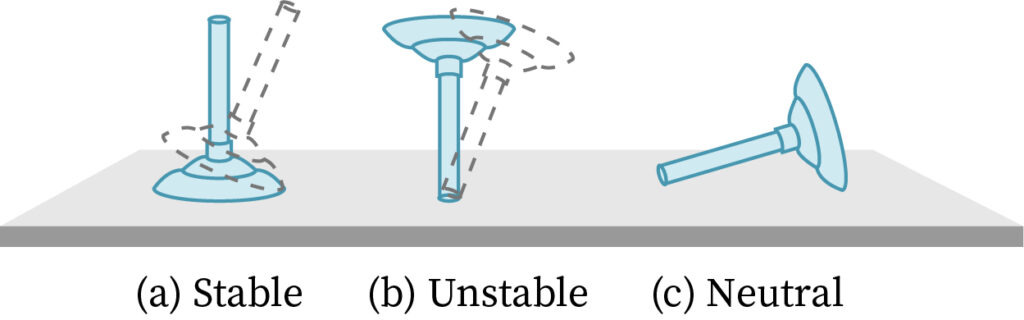
Types of Equilibrium seen in Rotational Dynamics
1) When the object tries to come back to the equilibrium state after its motion, the object is said to be in a stable equilibrium. This means the object has maximum potential energy.
2) When the object does not regain its position after its displacement then the object is said to be in an unstable equilibrium. This means the object tends to increase its potential energy.
3) When the object stays in its equilibrium position even after any external forces, then the object is said to be in a proper equilibrium state, hence the potential energy of the object remains the same. In Rotational dynamics, the work done is considered as the torque of the object moving in a rotational motion.
Application of Rotational Equilibrium and Rotational Dynamics
1) The electric fans undergo a rotational motion about their fixed axis and the forces acting upon it are considered under rotational mechanics.
2) The car's steering wheel is designed as per the rotational dynamics
3) The design, working operation, and the conversion of wind energy to mechanical energy inside a windmill also a good example of this motion
4) The revolving planets around the sun is due to the gravitation and rotational motions
5) Wheels, motors, gears, or anything that is designed for its circular motion
6) The merry-go-round in amusement theme parks is one of the classic examples where the rotational mechanics are carefully studied during the construction of it.
Practice Problems
1) Calculate the moment of inertia of a skater as per the following details mentioned
a) The 60 kg skater is approximated as a cylinder that has a 0.110 m radius. (b) The skater with arms extended approximately a cylinder of 52.5 kg has a 0,110 m radius and has two 0.900m long arms which are 3.75kh each and extend straight out from the cylinder like rods rotated about their ends.
Answer: a) Skater is considered as completely solid. The moment of inertia of a solid cylinder about the axis of geometry is given as
Substitute 60 Kg for mass and 0.110 m for radius into the formula to calculate the moment of inertia.
b) The moment of inertia for a solid cylinder about its geometric axis is
And the moment of inertia of a rod about its end is given as
In this case two hands spread out behave as two rods and trunk of body as a cylinder, thus the net moment of inertial is given as
Substitute 52.5 kg for mass of body, 3.75 kg for mass of the hands, 0.110 m for radius of the body and 0.900 m for the length of the hands to calculate the moment of inertia.
2) What happens to the angular momentum of the body during rotational motion when the time period is doubly increased but the moment of inertia remains the same?
Answer. The time period is inversely proportional to the angular momentum of a system if the moment of inertial remains the same. This is expressed as
Thus if the time period is doubly increased the angular momentum is reduced to half.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Science Physics
- Masters in Science Physics
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Rotational Equilibrium And Rotational Dynamics Homework Questions from Fellow Students
Browse our recently answered Rotational Equilibrium And Rotational Dynamics homework questions.