What is Rotational Mechanics?
An object or a rigid body or a particle has two ways of moving, one is in linear direction. The car running on the straight road means car travels in the linear direction. The second one is moving in rotational direction. While car running in linear direction, the wheels of the car rotate on its axis, the rotational movement of wheels are called Rotational Mechanics.
What is Rotational Motion?
Rotational Motion refers to any object spinning on its own axis or moving in a circular path. The movement can be uniform or non-uniform but it should move in circles. If an object moves in uniform motion, it has angular velocity in the movement. If an object has non- uniform movement, it is rotating in different angular velocity, hence it has angular acceleration.
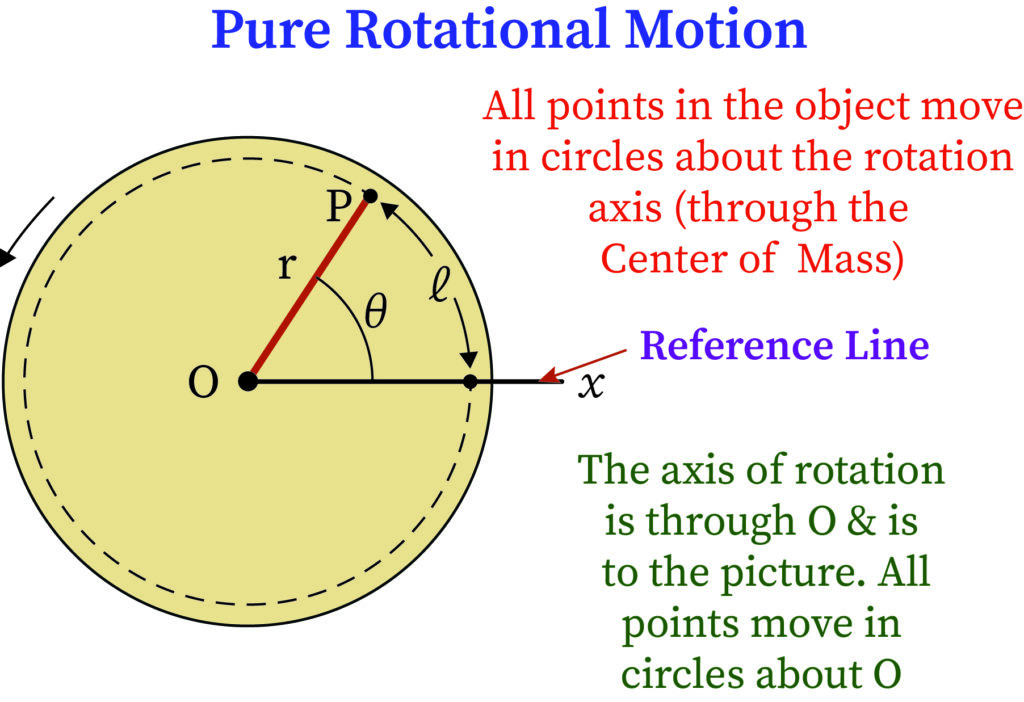
Comparison of Linear Velocity and Angular Velocity
Linear Velocity
A rate of change of linear displacement/distance of a body with respect to time is termed as linear velocity. With velocity the direction and distance can be predicted, hence it is a vector quantity. It is denoted as v.
Angular Velocity
A rate of change of angular displacement of an object is termed as angular velocity. It is denoted by letter omega (w). If an object is moving in circular motion or rotational motion at a uniform speed, the object has angular velocity.
It is also a vector quantity denoted by rad/s
- If displacement changes in meter it is linear velocity
- If displacement changes in angles or radian it is angular velocity
Comparison of Linear Acceleration and Angular Acceleration
Linear Acceleration
The change in linear velocity of a body with respect to time is known as linear acceleration. A difference in final velocity and initial velocity with respect to time is known as linear acceleration. It is also vector quantity, it is denoted by a.
a= (final velocity – initial velocity)/ time
Its dimension is m/s2
Angular Acceleration
It is the rate of change of angular velocity with respect to time. It is denoted by a(alpha).
It is denoted as rad/s2
- If velocity change is in m/s with respect to time it is linear acceleration
- If velocity change is in rad/s with respect to time it is angular acceleration.
What is an example of Rotational Motion?
Imagine playing a spinning wheel in the casino. While spinning the lucky wheel, it rotates and come to rest denoting 150 more spin for free as jackpot.

While spinning the wheel again and earning the same jackpot again, it means the spinning of the wheel is in same angular velocity. Hoping it is a case of rarity. While spinning for the third time, the wheel shows bankrupt, this means losing the money. Why couldn’t the spin be the same? The reason is having applied two different types of forces on the wheel, which resulted in two different type of angular velocity. Spinning the wheel in two different angular velocity means angular velocity is not uniform in the system. If there is change in angular velocity with respect to time, then it possesses angular acceleration.
Relation between Linear and Angular Quantities in Rotational Motion
The most important part of rotational motion is the relationship between linear motion and angular motion. Imagine a petrol engine stated, it will convert linear motion into angular motion. The linear acceleration of the piston is converted into angular acceleration in the crank shaft. There is a relationship between various motions; it’s an important definition to define the relation between linear and angular quantities of rotational motion.
Angular velocity, angular acceleration and angular displacement are interrelated by some physical law in mechanics.
Formulas
- ω: angular velocity
- α: angular acceleration
- θ: displacement in radian
- r: distance from axis of rotation
Torque
Due to non-uniform angular velocity, angular acceleration is created. This angular acceleration can be increased or decreased in rotational dynamics by magnitude of the torque.
Attach a spinning wheel with a rod at any face of the wheel, with that rod rotate the wheel, the wheel can be rotated in different pivot point. While holding the end part of the rod and spin it, due to maximum distance, the force multiplies as higher centripetal acceleration and increases the angular acceleration of the wheel. While holding at the last end of the rod the high magnitude of the torque is experienced. Getting closer to the wheel of the rod torque gets lesser.
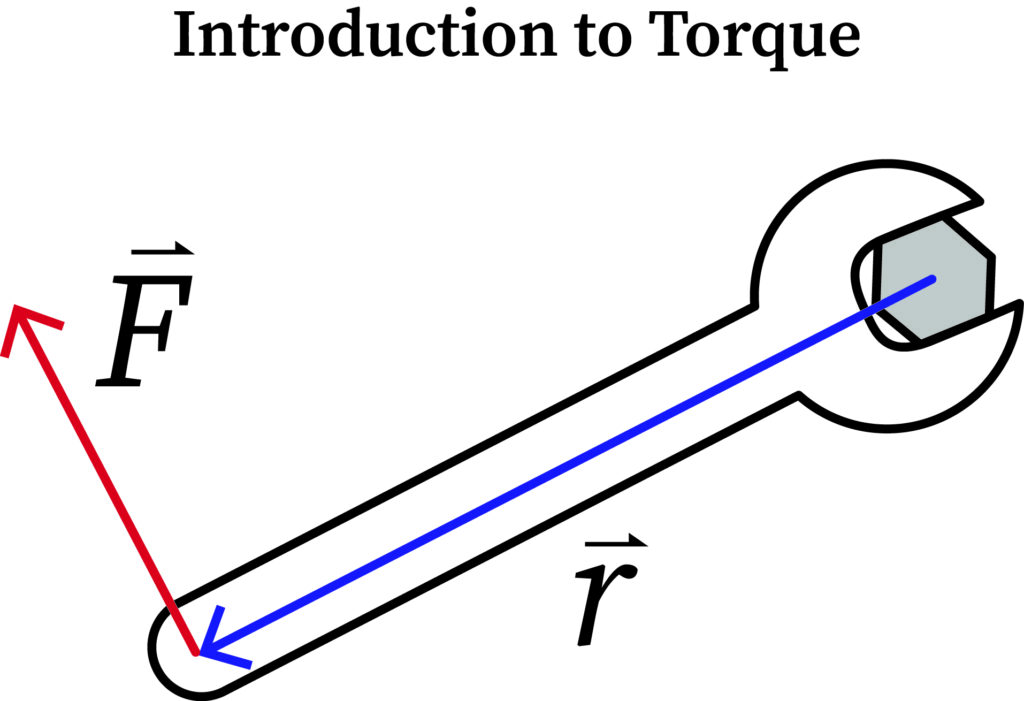
It is denoted as t, its unit is N-m
f- Force acting on object
r -Displacement vector pointing from the axis of rotation
Torque has magnitude and direction; it is determined by Flemings right hand rule.
When torque is applied to a rotating mass ‘m’ with acceleration ‘a’, it satisfies Newton’s Second Law condition.
F = ma
For rotating mass
F = τ
t is the torque. Thus torque is given by moment of inertia times angular acceleration
τ = I α
If a wheel is spinning in constant angular velocity, whose angular velocity vector is same then the wheel won’t experience any angular acceleration, if there is no angular acceleration, there is no net torque acting in the system.
Work, Energy and Power in Rotational Motion
A particle is displaced in space along a circular path, the energy supplied or work done by the particle is –
Work done is force (F) times displacement (r) which can be written as,
W = F r
Therefore in rotational motion,
Work done (W) = τ dθ
The rate at which work is done or power (P) = dW / dt
= τ dθ/ dt
But, dθ/ dτ = ω (angular velocity vector)
Therefore,
P = τ ω
Experience of this rotational motion or rotation dynamics in day today life is
- While studying this article eyeball experiences the rotational motion
- The watch in the hand
- Rolling of wheel
- Earth revolving sun
- Moon revolving earth.
- Giant wheel in amusement park
- Cycle wheel.
Context and Application
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science (Physics)
- Master of Science (Physics)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Rotational Mechanics Homework Questions from Fellow Students
Browse our recently answered Rotational Mechanics homework questions.