What are Scalars and Vectors?

Scalars and Vectors are the classification of physical quantities that are used to denote various terms in physics.

Scalars

Scalar is the quantities that are termed based on their magnitude or their physical size only. Every item has their different specifications. As with scalars, the specification magnitude is enough to define them. In short, scalars are the physical quantities that can be fully described with the help of a unit and number only. Hence, only magnitude is enough for defining a scalar quantity. In scalar quantities, every term works with respect to the addition law of algebra. Some of the basic examples of scalar quantities include time, length, mass, temperature, volume, energy, density, and so on. Each of these terms can be defined with magnitude only.

Vectors

In contrast to the scalar quantities, the vector quantities cannot be simply defined by using magnitude only. To get the complete specifications of a vector quantity, both the direction of the quantity and the magnitude are required. Most physical quantities can be termed as vectors, as they come with both magnitude and direction.

The additional law of geometry is obeyed by all vector quantities. This includes both the law of the parallelogram, and the law of the triangle. Usually, no vector quantities can be added by using the simple algebraic laws. Some of the basic examples of vector quantities include magnetic moment, force, acceleration, velocity, displacement, and so on.

Exceptions

The vector quantities must have a direction and magnitude to get their complete specifications. However, the reverse is not always true. This means that even if a quantity does have both magnitude and direction, there is no guarantee that the quantity must be a vector.

For example, electric current is not a vector quantity, despite having both direction and magnitude. This is because electric current fails to obey the law of vector addition. Upon addition, the resultant current obtained is less than the expected current. Hence, electric current is a scalar quantity instead of a vector quantity.

How is a Vector Represented?

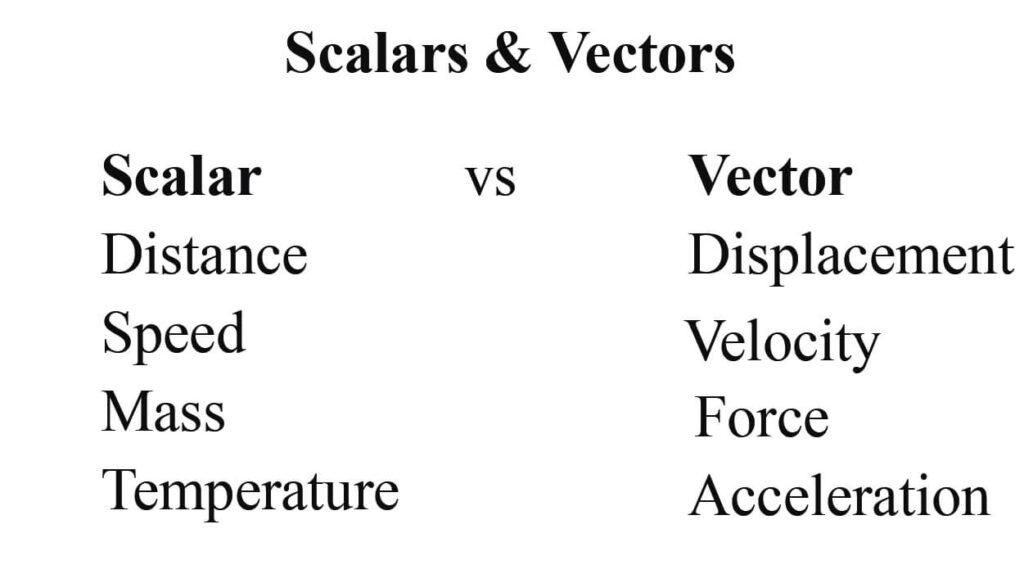
Since vectors have both directions and magnitude, any vector representation simply needs to have a direction marker. Usually, an arrowhead on a line over the notation of a vector quantity. The length and direction of the arrow is significant. The magnitude of the vector quantity is expressed with the arrow’s length, and the direction of the arrowhead represents which way the vector is directed to. For example, consider a displacement happening from a point P to Q. Then, the vector will be represented by-

To represent the vector graphically, then the two points A and B will be joined by a line segment which will be directed from the point A towards the point B. The direction of the arrow will represent the motion of the quantity, while the magnitude can be listed along the axes.

To summarize, a vector quantity can be represented by following the steps given below-

• Draw a line that will go parallel with the direction the vector is moving.
• The line’s length has to be cut, such that the magnitude can be expressed according to scale.
• The direction in which the vector quantity is moving should be clearly marked with an arrowhead.
• Simply write the vector quantity by putting an arrow on top the symbol.

What are the Types of Vectors?

Since vector is an actual physical quantity, the types are,

Unit Vectors

Vectors also come with a proper unit on them. However, there are special types of vectors as well. In a unit vector, the magnitude of the vector equals 1 or unity. It is solely used for denoting a direction that exists in space.

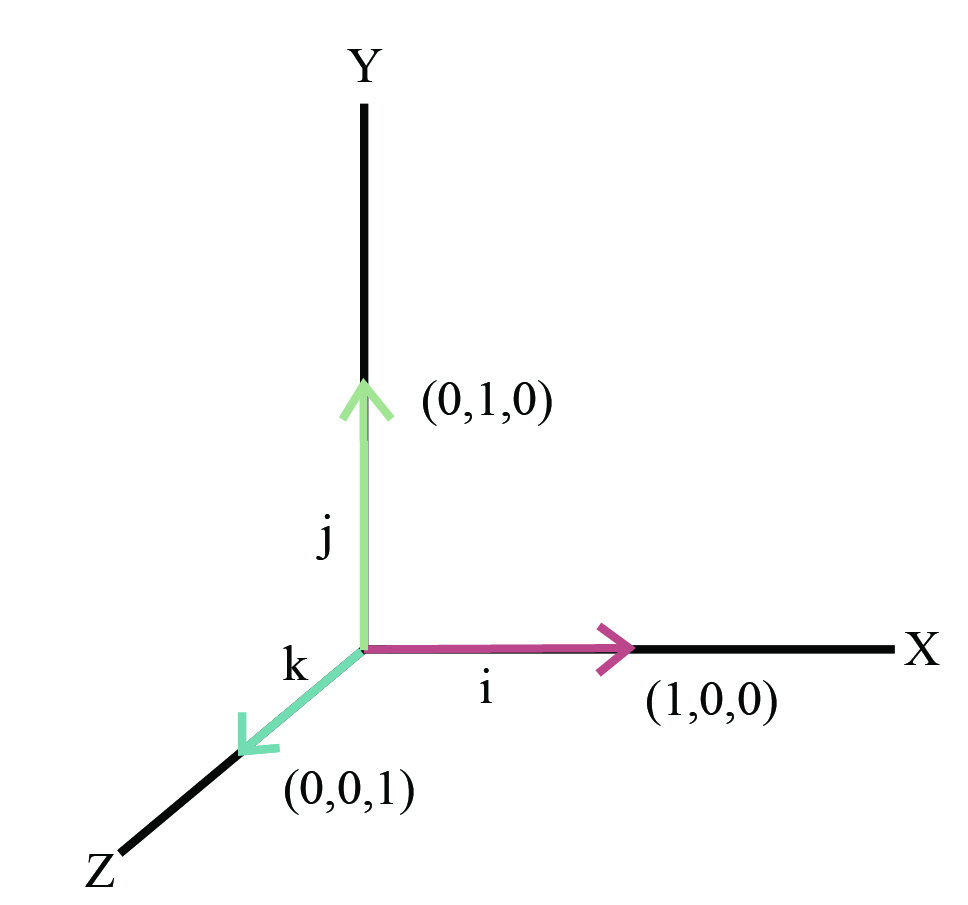
Consider a coordinate system of x-y, then a unit vector is represented by ‘$\widehat{\text{i}}$’, which is a vector that goes in the x direction, and the vector ‘$\widehat{\text{j}}$’ denotes the unit vector that goes in the y direction. Both of these unit vectors have a magnitude of 1.While the vectors are only considered, the vectors that exist in the x-y plane, then all of them can be represented with the help of these two-unit vectors.

While considering the three dimensions, then another unit vector ‘$\widehat{\text{k}}$’ will be added to signify the vector moving in z direction.

Collinear Vectors

In collinear vectors, there is a line of action which is common among the existing vectors. Collinear vectors are further divided into two types-

• Parallel Vectors
• Anti-parallel Vectors

Parallel Vectors

When two or multiple vectors are parallel according to one same line and they have the same direction, then the respective vectors are parallel to each other. In short, the angle between them is zero. In parallel vectors, the magnitude of the individual vectors does not matter.

Anti-Parallel Vectors

When two or multiple vectors are parallel in accordance with the same line, but have opposite directions, then these vectors can be termed as anti-parallel vectors. Here also the magnitude of the individual vectors holds no significance.

Equal Vectors

Among two or multiple vectors, if their direction and magnitude is same, then the corresponding vectors are said to be equal in nature.

Negative Vectors

Negative vectors have the same magnitude between them. However, their direction is opposite to each other. In such a pair of vectors, one vector is said to be the negative of the other vector.

Null Vectors

If a vector quantity has an arbitrary direction, and if the magnitude equals zero, them the vector is termed as a null vector or a zero vector. In such a vector, the distance between the start point and the end point is zero, or they both lie on the same point. Hence, the direction cannot be determined either.

Even if the concept of null vectors is hypothetical, it is used in vector addition and subtraction. Needless to say, and vector added or subtracted with a null vector retains its magnitude and direction.

Invariance of a Vector

If a vector quantity can be moved anywhere without any change in its direction or magnitude, then the vector is said to be invariant.

Co-Planar Vectors

The vectors that lie on the same plane are known as co-planar vectors. In co-planar vectors, the directions of the individual vectors do not matter.

Localized and Non-Localized Vectors

Any vector which has a fixed or localized initial point is known as a localized vector. Similarly, if the initial point of a vector is not fixed, it is a non-localized vector. Non-localized vectors are also known as free vectors.

Practice Problem

If vector a = (1, 2, 3) and vector b = (2, 3, 4), then find vector c, where $c=a+b$

Finding vector c is as follows:

Therefore, vector c = (3, 5, 7), which is the required answer.

Context and Application

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for   

• Bachelor in Science Mathematics
• Bachelor in Science Physics
• Master in Science Physics
• Master in Science Mathematics