What do you mean by Simple Pendulum?
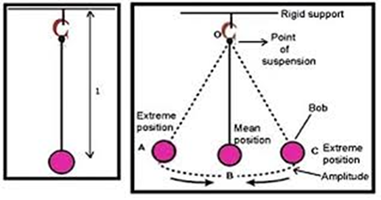
A simple pendulum comprises a heavy mass (called bob) attached to one end of the weightless and flexible string.
It can be defined as an object that moves back and forth by the action of gravity suspended from a fixed point by a light inextensible string. The mean position of a simple pendulum is the vertical line going through the fixed support.
The length of the simple pendulum is denoted by L and is considered the vertical distance between the suspension point and the centre of mass of the suspended body (when in the mean position).
Many engineered objects, like clocks, amusement park swings, metronomes, and earthquake seismometers, use pendulums. Studying the physics of pendulums' behavior is an important step in understanding motion, inertia, gravity, and centripetal force. To evaluate the force needed to propel an object into outer space, the braking power necessary to stop a vehicle at high speeds, and the highway ramp's optimum curve, engineers utilize their knowledge of these motion concepts.
Where do we use Pendulum Movement?
- In clocks, the most universally understood use of pendulums is experienced. Many clocks have a pendulum to measure time, most famously the "grandfather clock". At exact intervals defined by the length at which the pendulum is suspended, the pendulum swings back and forth. A pendulum clock must stay stationary to measure time effectively.
- The swing movement in the park is supported by chains attached to fixed points at the top of the swing set. When the swing is lifted and released, it will move back and forth freely due to the force of gravity on it. The swing continues to move back and forth without any additional external support until it is slowed down and finally stopped by friction.
Bowling Ball
How a pendulum's partial swing stores energy is seen by the swinging motion used in the bowl. On the backswing, you store the ball, and you store the energy in your arm. This is a result of raising the ball's weight against gravity. When you let the ball go, the energy is released, and thus it becomes the forward motion in the bowling lane.
Metronome
To maintain musical time, a mechanical metronome uses a pendulum swing. Metronome has an adjustable bob that can slide a strong arm up and down. Compared to a clock pendulum, it's arranged upside down; the swing time is longest when the bob is at the highest place.
Ball Wrecking
An example of pendulum movement is a wrecking ball that is used to demolish buildings. A professional crane operator swings the wrecking ball on a heavy rope, pointing it at the structure to be demolished. In the upswing, energy is retained and is released by the ball as something hits it.
Pendulums can be used to demonstrate that the earth is round. In a consistent pattern, pendulums swing and operate with gravity's intangible force, which varies due to altitude. The pendulum's moving pattern seems to change in a twenty-four-hour time frame if the pendulum is directly above the North Pole, but it does not. As the pendulum remains in the same plane of motion, the earth rotates.
The basic pendulums are quite interesting because they act as examples of simple harmonic motion, like springs or rubber bands.
A mechanical arrangement that demonstrates periodic motion is known as a simple pendulum which consists of a small bob suspended with a thin string. The bob is of mass "m", and the length of the string from the upper end to the platform is "L".
Terms related to Simple Pendulum
- Length: The distance between the center of the bob and the point of suspension denoted by "L" is known as the Length of a simple pendulum.
- The Time period: It is the time required for completing one full oscillation by the pendulum and is represented by "T'.
- The amplitude: It is the distance from the equilibrium position to one side travelled by the pendulum.
- Frequency: The number of oscillations performed per unit time is defined as the simple pendulum frequency.
- Pendulum motion
A pendulum motion is the movement of a mass suspended from a string that swings back and forth. The mass, the length of the string, and the position determined by an angle are the variables in a pendulum motion. Tension and gravity are the forces acting on the mass in a pendulum motion.
Simple Harmonic Motion
Simple Harmonic Motion is a type of periodic movementin which the restoring force is proportional to the displacement and acts oppositely. The position, acceleration, velocity, including an object in simple harmonic motion, are calculated using the simple harmonic motion formula.
Oscillatory motion
A periodic variation of a matter between two values or around its central value is also known as oscillation. The to-and-fro motion of a pendulum in a periodic pattern is known as oscillatory motion, and the equilibrium position is the center point of oscillation.
Small Angle Approximation
The small-angle approximation rule states that the trigonometric functions sine and tangent are approximately equal to the angle for small angles. Only when angles are calculated in radians is this approximation useful.
The three are completely equal only when the angle is zero. Symbolically represented as
θ≈ sin θ≈tanθ
Simple Harmonic Oscillator
An oscillator that is neither driven nor damped is known as a simple harmonic oscillator. It consists of a mass m that is subjected to a single force F that pulls the mass towards point x = 0 and is dependent only on the mass's position x and on the position x of the mass.
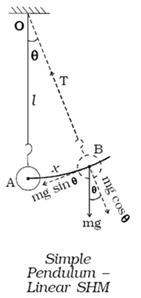
Simple Pendulum Time Period
Suppose there is an angle between the string of length l and the vertical is q. The bob's distance from the location of equilibrium A is AB. At B, weight mg acts downwards vertically. This force is divided into two components.
- The component mg cosq is balanced against the fixed point O by the string's tension working along the length.
- mg sin q, unbalanced, behaves perpendicular to the thread length of A. The bob continues to be returned to the mean position by this force. The path of the bob is a straight line if the oscillation amplitude is small,
∴ F = −mg sin θ …... (1)
If the angular displacement is small sin q ≈ q
F = −mg θ …... (2)
But we know that q = x/l
Thus, F = – mg (x/l)
After comparing this equation with Newton's second law,
F = ma
we get,
acceleration a = -gx/l …... (3)
The negative sign means that the acceleration direction is opposite to the displacement. Thus, the simple pendulum's motion is SHM.
We know that a = −ω2x
After comparing this with (3), we get,
w2 = g/l or
w = √(g/l) …... (4)
Time period, T = 2π/ω
The time period of a simple pendulum can be calculated by using the following formula,
The frequency of Simple Pendulum is calculated as
Where n= frequency of the pendulum
g= acceleration due to gravity
l= length of the pendulum
Laws of Pendulum
The following rules are articulated from the expression for the period of oscillations of a pendulum.
- The law of mass: A simple pendulum's time period is independent of the bob's mass and material.
- The law of length: The time period of a simple pendulum varies directly as the square root of the length of the pendulum.
- The law of acceleration: The period of a simple pendulum varies inversely as the square root of the acceleration due to gravity.
- The law of amplitude: The period of a simple pendulum is independent of the amplitude only if the amplitude is small.
Small Oscillations
When the energy of the system is very close to the value of the potential energy at the minimum, the system will undergo small oscillations about the minimum value x0. By using Taylor formula one can approximate the potential function as a polynomial. Near the minimum x0 the potential function can be approximated to a quadratic function and the system undergoes simple harmonic motion for small oscillations about the minimum x0.
Common Mistakes
- Students must remember that the time period is independent of the material of the bob.
- At the center of the earth, the value of 'g' is Zero.
- The time period of a pendulum placed inside an artificial satellite orbiting the earth is infinite as the value of 'g' inside the satellite is zero.
Context & Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- 10th,11th,12th Standard.
- Engineering Students
Few Applications of a simple pendulum are:
- In the process of hearing
- In earthquake-proof buildings
- In a clock
- Car shock absorbers
- Bungee jumping
- Musical instruments
Related Concepts
- Period of oscillation
- Seconds Pendulum
- Compound pendulum
- Clock pendulums
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Simple Pendulum Homework Questions from Fellow Students
Browse our recently answered Simple Pendulum homework questions.