What is Sound?
A sound is a form of vibration that travels through a medium in the form of mechanical waves. Sound waves are longitudinal waves that can travel through a propagation medium (which could be a gas, liquid, or solid).
Elastic properties of the respective medium help determine the speed of these waves.
What are Waves?

Waves are nothing but disturbances. Now, these disturbances are created or produced in different mediums.
A medium that allows the flow of signals through it is called a propagation medium.
A typical practical experience of such disturbance is to throw a stone in still water and observe the ripples. These ripples are disturbances that you created. The propagation of these ripples seems as if water is moving away from the central point of disturbance. But putting a lighter material on the disturbed surface, the material will vibrate up and down. This vibration is the proof that water isn't moving with the outward circles, but a moving disturbance is formed.
When we speak or produce sound from the sound source, the sound is sent across outwardly without the actual movement of air, rather the disturbances of the particles present propagate the signal. Unlike the obvious water waves and patterns, the depiction of disturbances in the air is much more complex and can't be seen through the naked eye. These vibrations, which systematically propagate without actual movement of particles, are called waves.
Propagation of Sound Waves
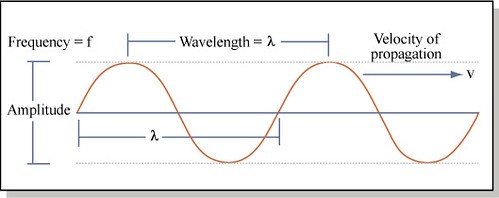
Sound waves are mechanical in nature, these vibration waves require a channel for propagation. Mechanical waves unlike electromagnetic waves require the presence of a channel to transport their energy.
As the wave passes through the air, it compresses or expands a small region.
To understand this, consider a collection of springs connected. If you pull spring at one end and suddenly release it, the disturbance travels to the other end. Why? As all springs were initially stable and under equilibrium, the first spring gets interrupted from its state of equilibrium length. Now the second spring is attached to the first, so it is also stretched/compressed, and this disturbance is carried from one edge to another, but each spring only shows minute oscillations about its equilibrium position. Different bogies of trains have spring attachments to each other. Engine at one end gives a push to the bogie next to it, and the push is passed on from one bogie to the next without displacing the entire train at once.
Back to sound waves, the compression and stretch cause a change in the density of that region, say δρ, this creates a change of air pressure by δp in that region. The relation between extension or compression of the spring with sound waves would be the change in density of pressure waves. If a portion of air is compressed, the air particles in that portion try to move out to the adjoining region, this consequently increases the density or creates compression in the adjacent region. Ultimately, the air in the first region undergoes a reduction in the density of that region. As this region is now comparatively rarefied. The neighboring air will rush in making the rarefaction move to the adjacent region. Thus, the compression/relaxation is transmitted from one place to another, and propagation of a disturbance is possibly achieved in air. Practically you can vibrate the tuning fork and hear the vibration and analyze how disturbances are being produced.
Figure 2 gives a 2D depiction of the three-dimensional phenomena occurring during the propagation of a wave.
Sound Waves are Longitudinal Waves
If constituents of a propagating channel vibrate along the direction of wave propagation, the waves are called longitudinal waves. In transverse waves, constituents vibrate perpendicular to the wave motion. Sound waves are assigned to the former category.
The perpendicular motion in transverse waves causes a change in shape and produces shear force, a force applied perpendicular to a surface, in opposition to a counter force acting in the opposite direction. Fluids have no shape, so they can combat this shearing stress, unlike solids. Hence transverse waves flow through fluids.
Longitudinal waves on the other hand involve compressive stress, which can be sustained by both fluids and solids, they can be propagated through solids, liquids, and gases likewise.
Characteristics of Sound Waves
We can define a sound wave by its frequency, amplitude, and speed.
We observe compressions and rarefactions in sound waves. the distance between two consecutive compressions or relaxations is called wavelength (λ)
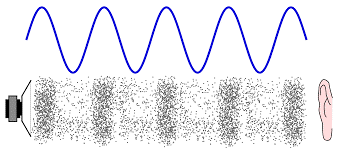
Frequency
Frequency (v) is measured by the number of waves passing through a fixed point in one unit of time. It is measured in hertz (Hz). When sound is propagating, density is changing from maxima to minima and then back to maxima, completing one cycle. The no. of such oscillations per unit time, v is
where T is the Time period. The sound's interpretation by our brain and analysis of its frequency is called its pitch. Faster the vibration of the source results in greater v and ultimately to a higher pitch. A high-pitched sound has more frequency than a low-pitched one. The audible v of sound for the human ear is between 20 Hz to 20000 Hz. Infrasound refers to the sound of frequency less than 20 Hz and Ultrasound denotes the sound of more than 20000 Hz, both of which require special equipment to be interpreted by the human ear.
Amplitude
The magnitude of the maximum disturbance from the mean position in the medium is called the amplitude (denoted by A) of the wave. The higher amplitude of sound waves also corresponds to higher sound energy, so the loudness and softness of a sound are related to amplitude. It depends on the force with which an object is made to vibrate. The light force will create a soft sound because we produce a sound wave of less energy (amplitude). If we hit any object hard we hear a loud sound. That sound would have greater energy so it travels more. The amplitude of a sound decreases as it moves away from the source.
Speed
Speed is the distance travelled by a point on compression waves or rarefaction waves, per unit time.
s=d/T
s=λv
As distance travelled by sound is wavelength and the inverse of time period is frequency.
The speed of waves in the propagating channel is different in different media. Highly compressed atoms in solids lead to higher s of sounds compared to that in fluids. This is because the lesser distance between particles leads to higher interaction and easier generation and transmission of disturbance. It is also dependent on temperature, it increases as we increase temperature.
| Substance (25ºC) | Speed(m/s) |
| Nickel | 6040 |
| Water (Distilled) | 1498 |
| Hydrogen | 1284 |
| Aluminum | 6420 |
| Ethanol | 1207 |
| Oxygen | 316 |
Common Mistakes
- The transmission of energy is confused with the movement of material as a whole.
- It should be noted that wind, which is the movement of entire air as a whole, is not equivalent to sound waves where there is the transmission of disturbance in the air, without motion of air as a whole.
Context and Applications
Applications of sound and waves, in general, are in the following field of study
Bachelor’s in science and Bachelors in Technology and Masters in science and Masters in Technology in Meteorology, Acoustical Engineering, Architectural Acoustics, Electroacoustics, Audio Engineering, etc.
Related Concepts
- Acoustics
- Vibration
- Doppler effect
Practice Problems
Q. The audible frequency range for normal hearing is from about 20 Hz to 20 kHz. What are the wavelengths of sound waves at these frequencies?
A. The wavelength and frequency of a wave are related by .
speed of sound s = 343 m/ sec
λ of 20 Hz = s/ v = (343 m/sec ) /(20.0 Hz)
= (343 m /sec ) /(20.0 /sec) = 17.2 m
λ of 20 kHz = s/ v = (343 m/sec ) /(20.0 kHz)
= (343 m s ) (20.0 /1000 sec) = 1.72 × 10−2 m = 1.72 cm
Q. A stone is dropped into a well. The sound of the splash is heard 3.1 sec later. What is the depth of the well?
A. The question deals with 2 time intervals: time for the stone to fall to the bottom and the time for the sound to travel back up to the listener.
The sum of these two times is: t1 + t2 = 3.1 sec (i)
If the depth of the well is d, then by equation of uniform motion we have s= ut+ 1/2 gt2 (ii)
now initial velocity u is 0, distance to be travelled is depth d, and time to reach the bottom t is t1, substituting in (ii)
d=1/2 g t1 2 = 1/2 (9.8) (t1 2) (iii)
Now, contrary to a stone's s , sound travels at a constant s ( assume it here as vs = 343 m/sec), it takes t2 time here to travel distance d
Vs t2 = d
343 t2 =d (iv)
from iii and iv 343 t2 = 1/2 (9.8) (t1 2)
4.9 t1 2 - 343 t2 =0 (v)
solving (i) and (v) you get t1=2.97 sec (avoid -ve root) , t2 =3.1-2.97=0.13 sec
d= 1/2 (9.8)(2.972)=44 m
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Sound Waves Homework Questions from Fellow Students
Browse our recently answered Sound Waves homework questions.