What is Resistance?
Electrical resistance or simply resistance is the property of a material that opposes the free flow of electrons through it. The total amount of resistance to the flow of charges (or current) is affected by many factors like the length of the conducting material, its cross-sectional area, resistivity, and temperature.
What is the electron theory of resistance?
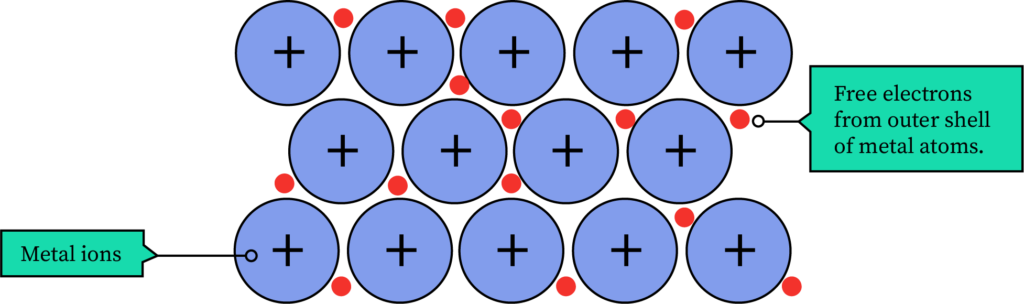
Metals have valence electrons at room temperature, which are free to move. These free electrons collide with each other and the metal ions. The collision and motion of the electrons are random. On applying a potential difference V across the metal, they tend to drift toward the positive direction, and their motion becomes almost directed. The collisions interrupt the movement of the charges, and this property is known as resistance, R.
The resistance of any material depends on the following factors:
- Length of the conducting material
- Nature of the material (number of free electrons per cubic meter)
- Area of the cross-section
- Temperature
The equation representing the dependency of resistance upon the above variables is given as:
... (1)
Here, ρ is the resistivity of the material, A is the cross-sectional area, and L is the length.
The SI unit of resistance is Ohm Ω.
Resistivity
Resistivity is the resistance of a material of a unit length and unit cross-sectional area. It depends on the nature of the material and its temperature. The SI unit of resistivity is Ohm-meter, Ω-m.
Relationship between Temperature and Resistance
While sitting in front of a room heater during winters, one can observe that as soon as the current starts flowing through the coil (electrical resistor), it becomes red hot. This happens because of the resistance of the conductor. When the heater is switched ON, the flow of charges (hence, current) across the conductor gets obstructed by the resistance of the conductor. When the temperature increases, the atoms and molecules acquire a larger amount of thermal energy; thus, their vibrational motion also increases. As a result, the resistance also increases, and the coil becomes hot.
The resistance of any material depends directly on its temperature. With an increase in temperature, the resistance also increases. Carbon is an exceptional case where the resistance decreases with an increase in temperature. The temperature coefficient of resistance (commonly known as temperature coefficient of resistivity) establishes a relationship between temperature and resistance. It is usually denoted by α.
Variation in resistance of a material at different temperatures
An increase in the resistance of a material due to a temperature change is directly proportional to its resistance.
... (2)
An increase in resistance is also directly proportional to the change in temperature.
... (3)
From equations (2) and (3),
... (4)
Here, α is known as the temperature coefficient of resistance (TCR).
Let be the final resistance and be the final temperature. Then,
From equation (4), we get:
... (5)
Suppose the resistance of a material at 0∘C is R0 and at T∘C the resistance is RT.
... (6)
Thus, temperature coefficient can be defined as the fractional change in the resistance of a given material per unit of the original resistance that occurs per degree change in temperature. The unit of temperature coefficient is or .
From equation (1), it can be deduced that the resistivity ρ depends on the temperature increase. Therefore, equation (5) can be written as follows:
... (7)
Effect of temperature on the resistance of a conductor
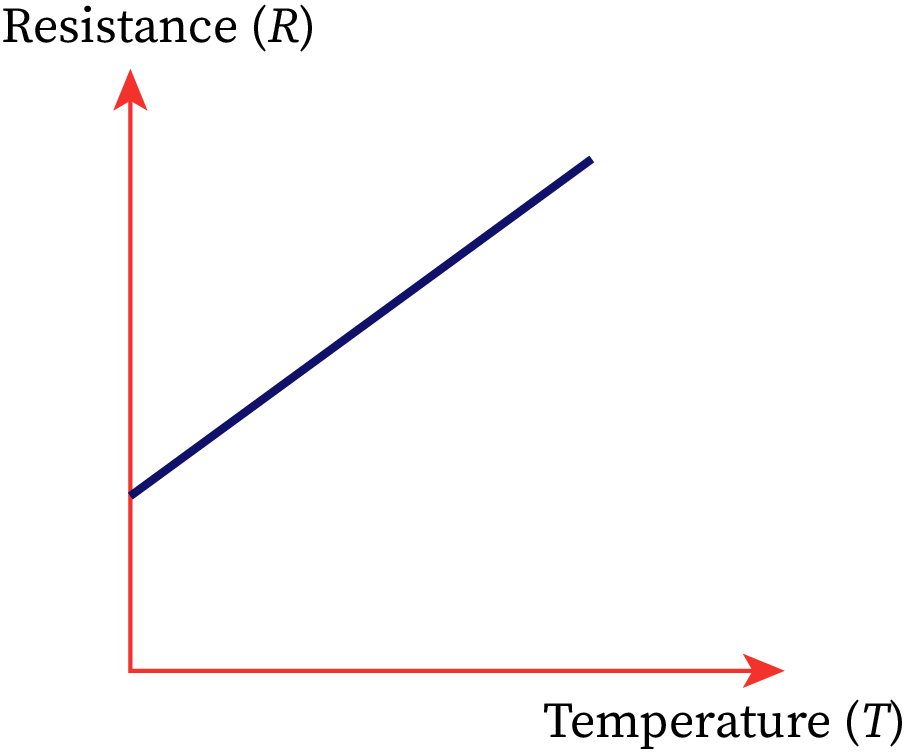
The resistance of a conductor depends on various factors. These are the nature of the conductor, the size of the conductor, and physical conditions like temperature. The effect of temperature on a metallic conductor is directly proportional to its resistance. Over a defined range of temperatures, with an increase in temperature, the resistance of metals increases linearly.
At low temperatures, the metal ions are almost stationary. When the temperature increases, these ions collide with the free electrons of the metals. Each collision consumes some energy from the free electrons and is the primary cause of resistance. The vibrations about the mean positions increase, which hinders the movement of the electrons, and hence, greater resistance to the current flow occurs.
Generally, conductors have a positive temperature coefficient of resistance. Some examples of conductors are aluminum, silver, copper, gold, iron, etc.
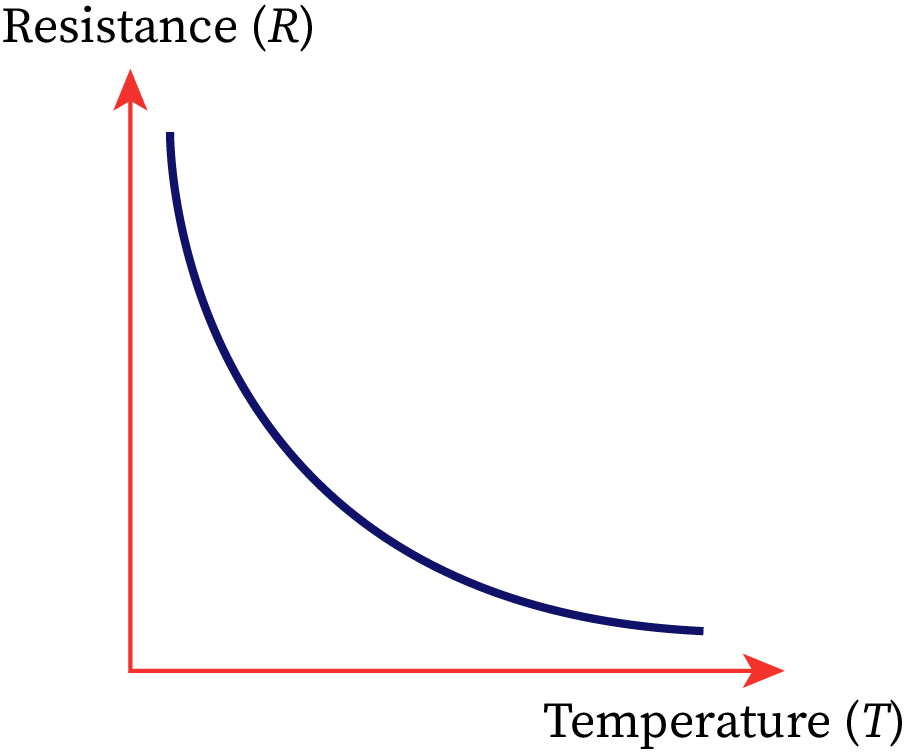
Effect of temperature on the resistance of a semi-conductor
The forbidden energy gap EG between the condition band and valence band is very small in a semiconductor. On applying external heat to a semiconductor, the atoms’ bond strength is broken, and it becomes easier for the electrons to jump from the valence band to the conduction band, thus increasing the conductivity of the semiconductor.
The conductivity of any material is inversely proportional to the resistivity and hence, resistance. Thus, on increasing the temperature of a semiconductor, the resistance to the flow of electrons decreases. Some examples of semiconductors are silicon, germanium, gallium arsenide, etc. They have a negative temperature coefficient of resistance.
On the manipulation of this theory, a resistor can be made whose resistance is independent of temperature. Two resistors, one having a positive TCR and the other with a negative TCR, are connected in series and have an equivalent resistance, which is R. The values of the resistances are chosen in such a way that with any change in temperature, the increase in resistance of the first resistor is nullified by the decrease in the resistance experienced by the second resistor.
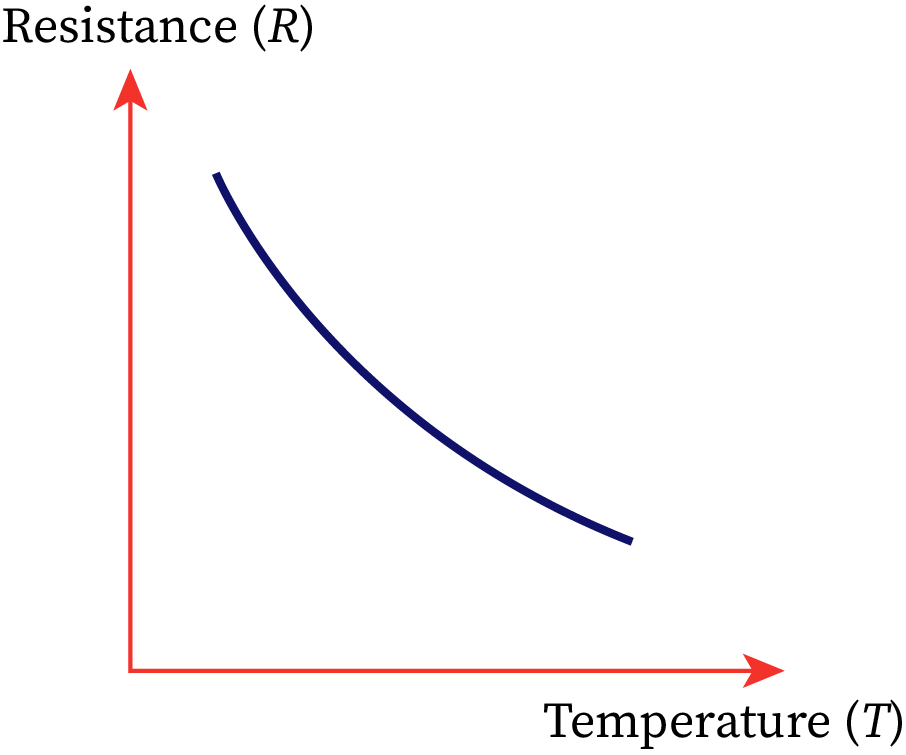
Effect of temperature on the resistance of an insulator
The forbidden energy gap between the conduction band and valence band of an insulator is significantly very large compared to a semiconductor. The electrons in the insulators are tightly bound to the nucleus, and it is difficult to break the bonding between the atoms. The valence electrons cannot easily bridge the energy gap. Thus, conduction is nearly impossible.
The increase in temperature reduces the band gap energy to some extent, and the electrons jump from the valence band to the conduction band. Thus, the conductivity of the insulator increases, and the resistance decreases. It has a low negative temperature coefficient of resistance (at high temperatures). Some examples of insulators are plastic, glass, rubber, paper, etc.
Effect of temperature on the resistance of an alloy
The resistance of an alloy remains almost unaffected by any change in its temperature. In alloys like constantan (commonly called Eureka) and manganin, the arrangement of atoms is disordered, and they have high resistivity. On increasing the temperature, the additional disorder is negligible. Thus, the resistance of an alloy has no temperature dependence.
Common Mistakes
Students often assume that conductors are always in solid form. However, liquids can also be good conductors, and most liquids that conduct electricity are bases, acids, and salts. For any solution to conduct, there must be a presence of ions or free electrons. Moreover, the resistance of liquid conductors and electrolytes decreases when the temperature is increased.
Also, there is a misconception that all materials follow Ohm’s law which is not true. The resistance of a semiconductor or an electrolyte is non-ohmic, i.e., it does not follow Ohm’s law.
Formulas
- The resistance, R of any material is given by the equation, . Here, A is the cross-sectional area, L is the length, and is the resistivity.
- The temperature coefficient of resistance, is given by, . Here, the resistance of the material at temperature is and at temperature the resistance is RT.
- The relation between the resistivity of a material and its temperature coefficient is given by, . Here, is the resistivity of the material at temperature and is the resistivity at temperature .
Context and Applications
This topic is significant to various professional exams for undergraduate courses such as:
Master of Science in Applied Physics
Bachelor of Engineering in Electrical Engineering
Bachelor of Engineering in Civil Engineering
Related Concepts
Electric Current
Electric Potential Difference
Charge Carriers
Conductance
Resistivity
Practice Problems
Q1: The resistance of any resistor decreases if:
(a) The number of free electrons or ions increases
(b) The temperature decreases
(c) The temperature increases
(d) None of the above
Correct option: (a)
Q2: What is the unit of temperature coefficient of resistance?
(a)
(b)
(c)
(d)
Correct option: (b)
Q3: Which of the following statements is true regarding insulators?
(a) Insulators have a negative temperature coefficient of resistance.
(b) Insulators have a zero temperature coefficient of resistance.
(c) Insulators have an infinite temperature coefficient of resistance.
(d) Insulators have a positive temperature coefficient of resistance.
Correct option: (a)
Q4. The metallic conductors have,
(a) A negative temperature coefficient of resistance.
(b) Zero temperature coefficient of resistance.
(c) An infinite positive temperature coefficient of resistance.
(d) A positive temperature coefficient of resistance.
Correct option: (d)
Q5: The resistance of a copper winding at room temperature is 200 Ω. The temperature co-efficient of resistance for copper is . If the temperature is increased to , then the resistance of the winding will be:
(a) 245.19 Ω
(b) 201.07 Ω
(c) 217.12 Ω
(d) 222.54 Ω
Correct option: (c)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Temperature Variance of Resistance Homework Questions from Fellow Students
Browse our recently answered Temperature Variance of Resistance homework questions.