What is Bohr's model?
Niels Bohr proposed the model of an atom in 1915. His model is based on the laws of classical physics and quantum mechanics. This model overcomes the drawbacks of Rutherford's model of an atom. With this model, Bohr succeeded in explaining the stability of an atom.
What are the postulates of Bohr's model?
The important postulates of Bohr's model of the atom are the following:
- According to Niels Bohr, the nucleus of an atom contains neutrons and protons.
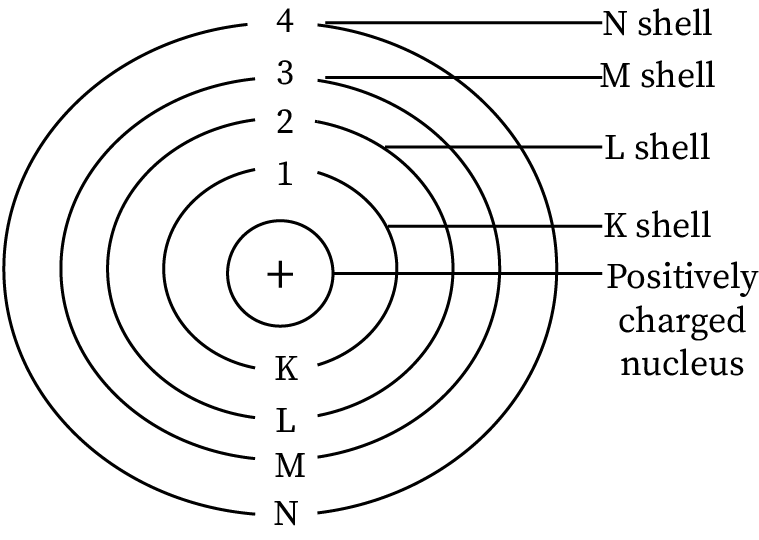
- Orbits are circular paths in which electrons revolve around the nucleus.
- The angular momentum of electrons is quantized in their orbits. It is an integral multiple of .
- The centripetal force gives the force of attraction between the positively charged nucleus and the negatively charged electron.
- It lies at the center of an atom.
- The electron orbits have a definite amount of energy.
Sketch of Bohr's model
Determination of Bohr’s orbit from the Bohr’s model
Assume the mass of an electron is “m,” and its charge is “e.” The charge on the nucleus is “Ze” (where Z is the atomic number). Let the tangential velocity of the electron be “v” and the radius of electron orbits be “r”.
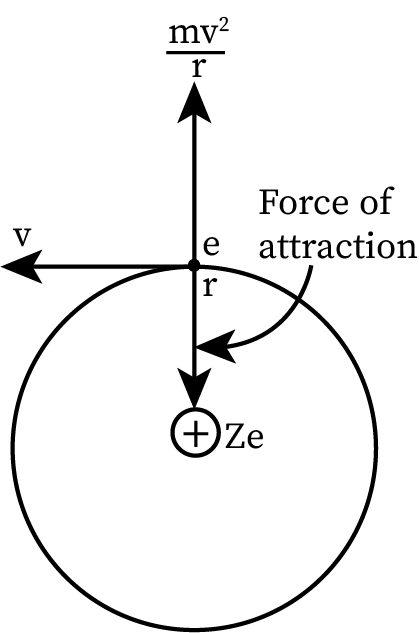
The formula for the electrostatic force between the negatively charged electrons and the positively charged nucleus is:
...(1)
The centripetal force acting on circular orbits is:
...(2)
From Bohr's postulates, electrostatic forces and centripetal forces are equal.
...(3)
From equation (3):
...(4)
From Bohr's quantization of angular momentum,
...(5)
Here,
h = Planck' s constant and n = orbit number
From equation (5),
...(6)
From equation (4) and (6), the expression for Bohr radius is:
...(7)
Here, Electrostatic constant .
The radius of the nth orbit for a hydrogen atom can be calculated using the above formula.
Atomic number is Z =1
Charge
Planck's Constant
Mass of electron,
Value of pie π=3.14
Substituting all the values in equation (7), the Bohr radius for the hydrogen atom is:
For the hydrogen atom, n = 1 corresponds to the ground state.
The radius of an electron in the ground state is
Also, n =2 corresponds to the first excited state.
The radius of an electron in the first excited state is
The energy of an atom
The formula for the kinetic energy of an electron,
The potential energy of an electron, .
The total energy of an electron is:
....(8)
Substitute the value of mv2 from equation (4) and the value of radius r from equation (7) in equation (8).
The total energy of the electron is:
...(9)
Here,
For the hydrogen atom, atomic number, Z =1
Substituting the values of all constants in equation (9), for the hydrogen atom, the energy of an electron is:
...(10)
For a hydrogen atom, the ground state energy is . (Substitute n =1 in equation 10)
The energy of an electron for a hydrogen atom in the first excited state is . (Substitute n =2 in equation 10)
The energy state equation of hydrogen-like atoms is .
Rydberg formula
Consider and to be the two energy shells in the hydrogen atom.
For the first shell, the energy of electrons is:
...(11)
The energy of electrons in the n2 shell is:
...(12)
Subtracting equation (12) from equation (11):
...(13)
Photon is a packet of energy. Excess energy is emitted as a photon when the transition occurs from higher to lower orbits. Each photon propagates with the velocity of light in vacuum.
The energy of the emitted radiation for a photon is:
...(14)
Here, λ is the wavelength and c is the speed of light in vacuum.
From equation (13) and (14):
...(16)
Here, is Rydberg constant.
Drawbacks of Bohr model
- Bohr's model cannot explain the atomic spectra of many-electron atoms.
- This theory also cannot explain the fine spectrum of a hydrogen atom.
- It also fails to explain the splitting of spectral lines due to magnetic and electric fields.
- This theory does not give justification to de-Broglie's dual nature of matter.
- It cannot provide an explanation for Heisenberg's uncertainty principle.
- It gives no explanation for the three-dimensional model of an atom.
- In this theory, there is no explanation for the shapes of molecules.
Common Mistakes
Students often get confused between Rutherford’s model and Bohr model of an atom. They interpret the postulates of both these models to be the same, which is incorrect. Rutherford’s model differs from Bohr’s model in the following ways:
- Rutherford's model does not give any explanation for discrete energy levels, whereas Bohr's model explains the presence of discrete energy levels.
- Rutherford’s model does not give the formula for the energy and radius of an electron in the orbit, while Bohr’s model gives the expression for radius and energy.
- Rutherford's model cannot explain the stability of an atom, whereas Bohr’s model explains it.
Context and Applications
This topic is significant in the professional exams for both graduate and undergraduate courses especially for:
- Bachelor of Technology in Chemical Engineering
- Bachelor of Science in Physics
- Master of Science in Chemistry
- Master of Science in Applied Chemistry
- Quantum Mechanics
Related Concepts
- Rydberg Formula
- Hydrogen Spectrum
- Ionization Energy
- Electromagnetic Radiation
- Model of the Hydrogen Atom
- Rutherford-Bohr
Practice Problems
Q1: Which principle was used by Bohr to explain his model?
- Conservation of linear momentum
- Conservation of energy
- Conservation of angular momentum
- Conservation of quantum frequency
Correct option: (c)
Q2: If the principle quantum number increases, the energy difference between two consecutive levels
- First decreases then increases
- Decreases
- Increases
- First increases then decreases
Correct option: (b)
Q3: The necessary centripetal force required by an electron to move around the nucleus in circular orbits is provided by
- Strong nuclear force
- Gravitational force
- Weak nuclear force
- Electrostatic force
Correct option: (d)
Q4: When an electron transits from a higher energy level to a lower energy level, the energy gets
- Radiated
- Absorbed
- Reflected
- Both (a) and (b)
Correct option: (a)
Q5: In a hydrogen atom, for radius of nth Bohr orbit, r which of the following relations is correct?
Correct option: (a)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
The Bohr model Homework Questions from Fellow Students
Browse our recently answered The Bohr model homework questions.