What are Units?
These are generally defined as the terms which precede or describes the dimensions further. These are also further divided into two parts namely fundamental units and the derived units.
Fundamental Units
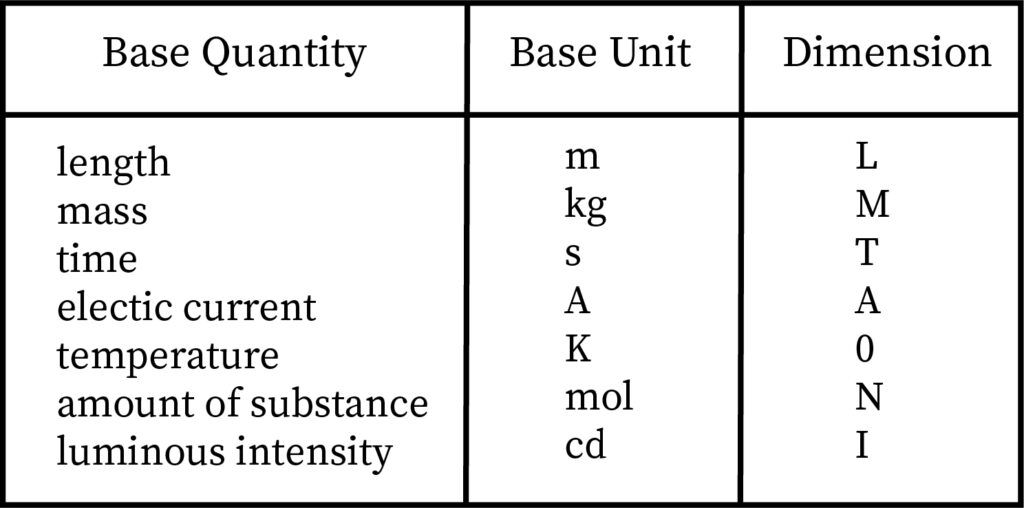
The quantities that are not depended on some other quantities are called as fundamental quantities and the units which are basically used to measure these quantities are known as fundamental units. And these system of units can be further classified as SI, CGS, MKS and FPS.
For example- to calculate the fundamental quantity i.e. length, mass and time. In CGS, unit of length can be given as centimetre, mass as gram and time as second. In case of MKS, they can be given as meter, kilogram and second respectively and in case of FPS as foot, pound and second, in SI as meter, kilogram and second respectively.
SI system is the most widely used system to measure and it also been used in the scientific research.
Derived Units
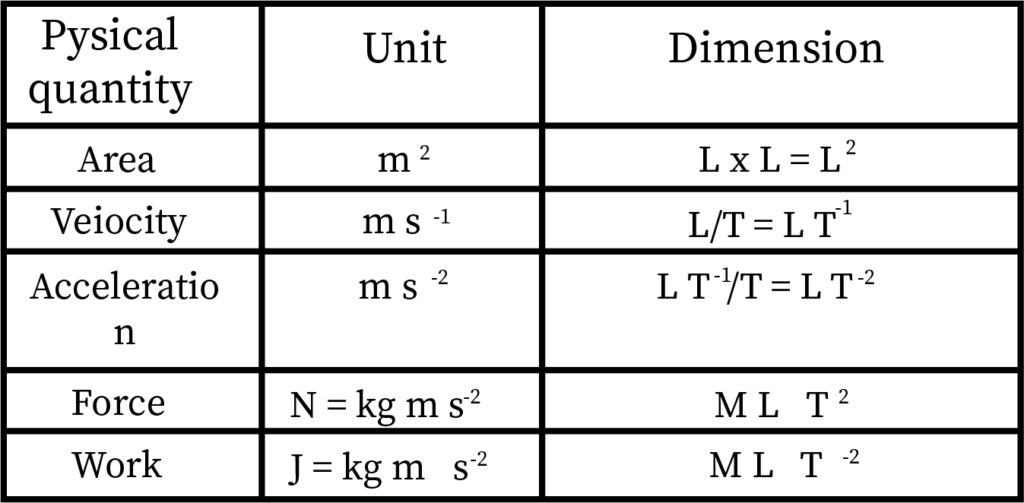
The quantities which are depended on the fundamental quantities for their existence, such type of quantities are called derived quantities and the units which are used to measure such type of quantities are known as the derived units.
Units Used
Meter- There are many definitions have been provided for one meter since a long time but the modern definition says that the distance which has been travelled by the light while in vacuum in the time interval of 1/ 299,792,458 of a second.
Kilogram- It is defined by the International Bureau of weights and measures as the mass of a cylinder which is made up of Platinum-Iridium alloy which is kept there.
Second- It is defined as the duration of 9192631770 periods of radiation which is corresponding in between the two hyperfine levels of the cesium-133 atoms at the ground level.
Ampere- It is defined when the current which is flowing through the two parallel conductors which are having the infinite length and the negligible cross sectional area and which are at a distance of 1 meter apart from each other and causing the force of 2x 10-7N for a unit meter of length.
Way of Writing the Unit of Physical Quantities
- They should be written with complete name or can be written as the defined symbols only.
- They must not be written in a plural form like- only 10kg not like 10kgs.
- They must not be written with a full stop or any kind of punctuation mark. Example- 10 W only and not like 10W.
What are Dimensions?
It is defined as the property which shows the relationship between the various types of physical quantities with the help of base quantities.
Dimensional formula
It is the expression which shows the powers to which all the fundamental quantities are raised to obtain the unit for the derived quantity. It can be expressed in the form of MaLbTc. In this, M stands for mass, L stands for Length and T stands for time.Like energy can be written as ML2T-2.
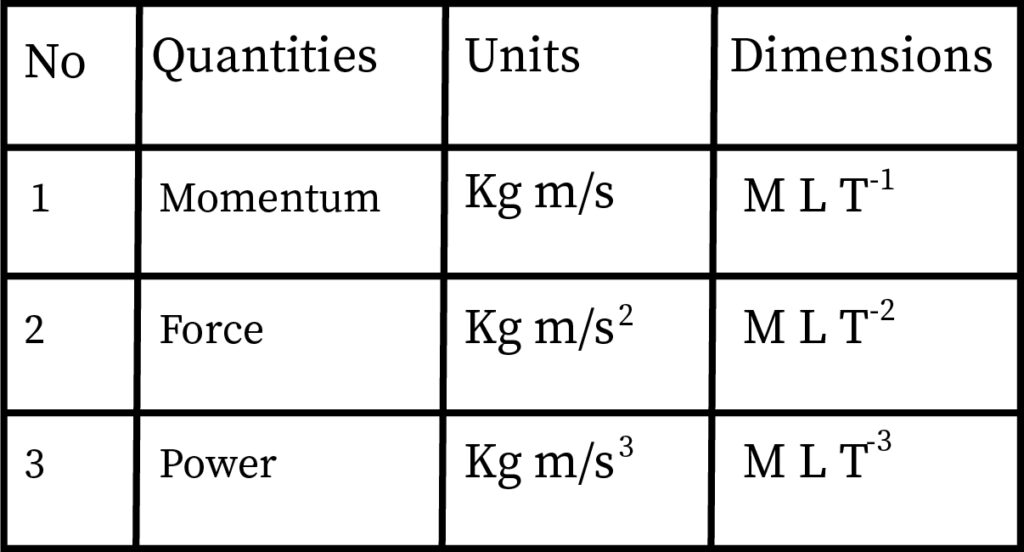
Some quantities have same formula, which includes- momentum and impulse, force and thrust, power and luminous flux, stress and pressure and many more.
Dimensional Constants
There are certain physical quantities which can be expressed as the dimensions but they also have some fixed values, they are referred to as dimensional constants. Some of these includes- Gravitational constant which is denoted with G, Plank’s Constant which is denoted with h, Universal gas constant which is denoted with R, speed of light which is denoted with C, etc.
Dimensionless Quantities
These are defined as the quantities having a fixed value but they do not have any kind of dimensions. They are of two types which includes- dimensionless quantities without units and the dimensionless quantities with units.
Dimensionless quantities which do not have units include- Pure numbers, π, e, sin θ, cos θ etc.
Dimensionless quantities which have units include- Angular displacement which is taken as radian, Joule’s constant which can be taken as Joule/ calorie.
Dimensional variables
These can be described as the physicals quantities which are having dimensions but are not having any fixed value. Examples include- Acceleration, work, force, power, velocity etc.
Dimensionless variables
These can be described as the physical quantities which are having no dimensions and are not having any fixed value. Examples include- specific gravity, poison's ratio, co-efficient of friction etc.
Law of Homogeneity of the Dimensions
- This states that for any equation which is representing the relationship between the physical quantities should have equal number of terms of dimensions on both of its sides and the terms which are separated with the positive or negative sign, they too must have the same dimensions.
- This can also be seen with the help of an example as any system which is having physical quantity P which is having dimensions i.e. a, b and c in length (L), mass (M) and time (T) respectively and are having fundamental units as L1, M1 and T1 and is having a numerical value n1. While the fundamental units in the other system is L2, M2 and T2 respectively and are having the numerical value as n2. This can be written as-
n2= n1x [L1/L2]a [M1/M2]b [T1/T2]c
Limitations related to Dimensional Analysis
- This law is not valid for the quantities which are dimensionless in nature. There is no outcome for any kind of proportionality can in this method. This can only be found with the help of experiment or the theory.
- This law is not valid for the functions which are logarithmic, trigonometric or exponential in nature.
- When all the three physical quantities are dependent on each other, then in that case, this law will act as difficult in nature.
- Sometimes, proportionality constants also contain the dimensions, in such cases where the dimensions are there for the proportionality, we cannot use such system.
- When there is any sign of positive or negative to only one side of the equation, then in that case this law is inapplicable for finding out the expression.
Context and Application
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Science
- Masters in Science
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Units and Dimensions Homework Questions from Fellow Students
Browse our recently answered Units and Dimensions homework questions.