What is pressure?
Pressure is defined as the perpendicular force per unit area exerted to the surface of an object or the stress per unit area in the case of fluids. When force F (in Newton) is applied perpendicular to area A (in unit of m2) the pressure acting on the surface is the ratio of the applied force and the area of the body, i.e.,
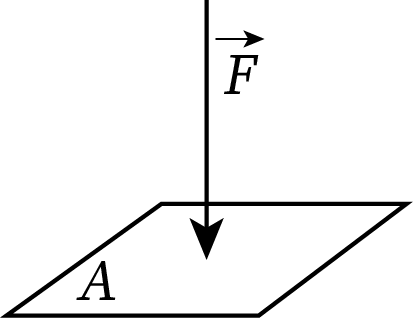
The SI unit of force is Pascal, which is denoted as Pa. One Pascal is defined as the pressure experienced by a surface of unit area when a force of one Newton is applied.
Variation of pressure with applied force
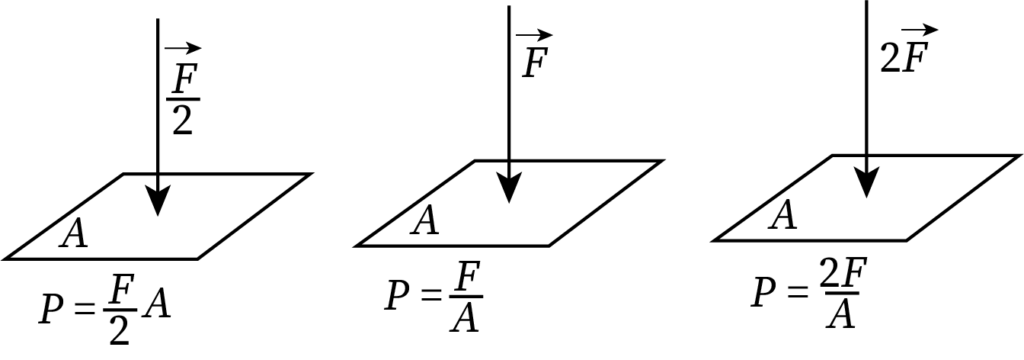
From the equation of pressure, pressure is directly proportional to the applied force.
When the surface area of a body is constant, the pressure increases by increasing the force and decreases with decreasing force.
The following figure shows how pressure varies when force becomes half and double of its initial value (surface area remains constant).
Variation of pressure with surface area
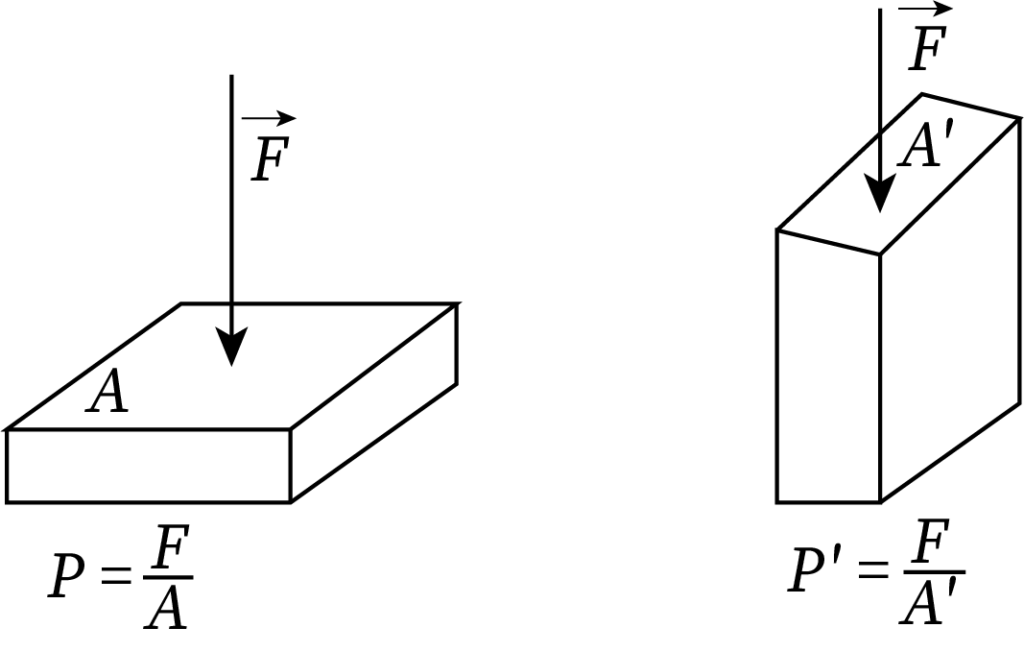
From the equation of pressure, pressure is inversely proportional to the surface area of the body.
When the applied force is constant, the pressure increases with a decrease in the surface area and vice versa.
The following figure shows the pressure acting on two sides of a rectangular box. Here, surface area A is more than A'. Thus, the pressure experienced at the second surface area is greater than at the first one.
What is Fluid pressure?
Fluid pressure is the pressure that arises due to the weight of fluid at a specific point. Here, the force is the weight of fluid (gravitational force).
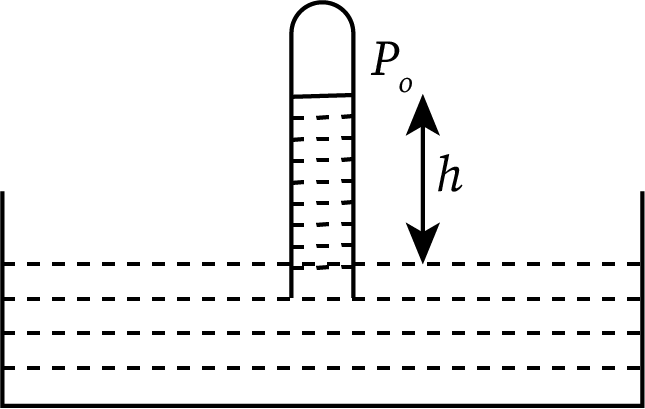
This fluid pressure depends on the atmospheric pressure, the density and height of the given fluid, and acceleration due to gravity. The relation for the pressure of a fluid at height h is:
Where, is the atmospheric pressure, g is the acceleration due to gravity , h is the height of fluid and is the density of the fluid.
The density of a stationary fluid is the mass per unit volume.
Then the equation for pressure becomes:
From these equations, fluid pressure is directly proportional to atmospheric pressure, acceleration due to gravity, and density, height, and mass of the given fluid. Also, it is inversely proportional to the volume of the given fluid.
How pressure varies with depth?
A fluid exerts the same amount of pressure in all directions. By the concept of surface tension of fluids, horizontal tension appears on the top layer of the liquid due to the cohesive nature of molecules. In the case of water in a beaker, the top layer of water on the beaker will exert a pressure on the side wall of beaker, layer of water at the bottom level and on the layer of air molecules at the top of this surface layer. From top to bottom in the beaker, the pressure exerted by a layer on the layer below it adds up. Thus, there is an increase in pressure as we move from top to bottom in a fluid.
The pressure exerted by the fluid at equilibrium condition, at a particular time, due to gravity is called the hydrostatic pressure. A simple experiment for better understanding variation of fluid pressure with depth is making holes in a water-filled beaker at different points. The arrangement is shown in the following figure.
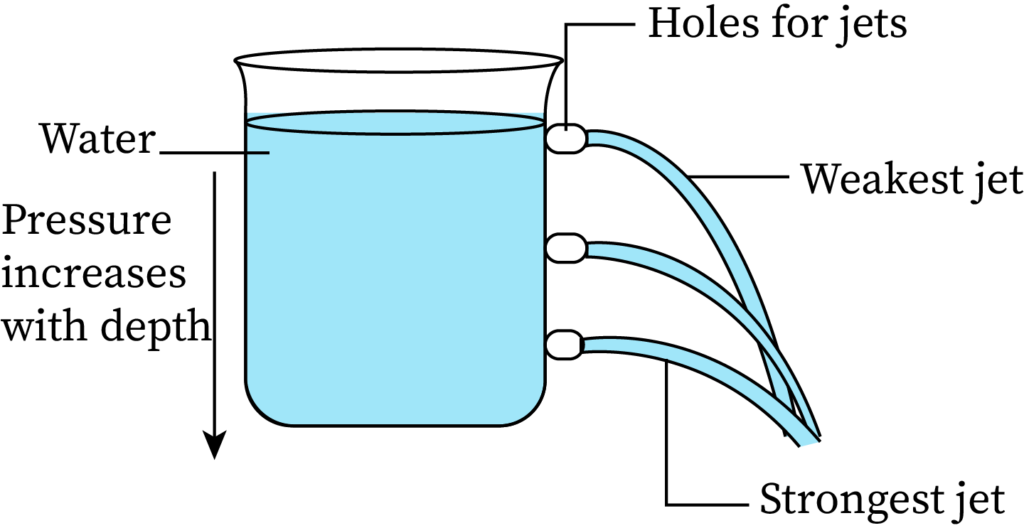
Here, water ejects from the lowest hole at a higher velocity than from other holes at higher positions. The water from the lowest hole also covers the maximum horizontal distance. This proves that the pressure is higher at the bottom than at the top, or that the pressure increases with an increase in the depth of the fluid.
An example of this is during deep diving in a swimming pool. When you enter inside the water, you experience more pressure with depth.
How pressure varies with height?
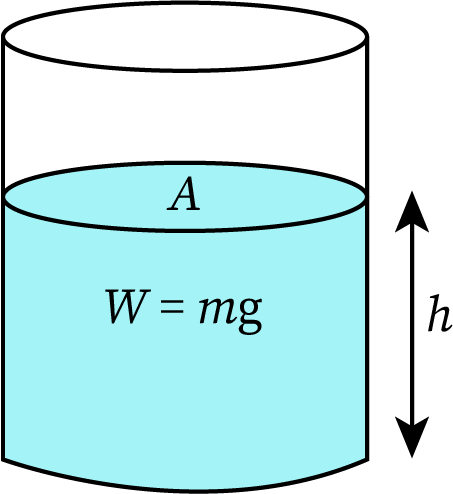
The pressure due to any fluid is the force per unit area. The force exerted on a liquid in a container is gravity or the weight of the liquid (product of the mass of the liquid and acceleration due to gravity). Then,
The density of a fluid is the mass per unit volume. And mass is the product of the density and volume of the fluid.
Then, the volume of the fluid is the product of its surface area and height.
The weight of the fluid is:
Applying this value in the equation of pressure,
This relation shows that the pressure of a fluid is directly proportional to its height. When height increase, the pressure of the fluid also increases and vice versa.
An example of this is when you go hiking, you can feel the air pressure difference between the top and the base of the hill. You can also feel this variation while traveling on a flight.
How pressure varies with temperature?
According to Amonton’s law, the pressure of an ideal gas varies directly with its temperature at a constant volume.
The ideal gas equation is:
Here, n is the number of moles, and R is the universal gas constant with the value, .
From the above relation, pressure is:
Similarly, for a fluid with a constant volume, the pressure is directly proportional to the temperature of the fluid. That is:
Thus,
When the temperature of a system increases, its pressure also increases and vice versa. The pressure versus temperature graph at constant volume is given below.
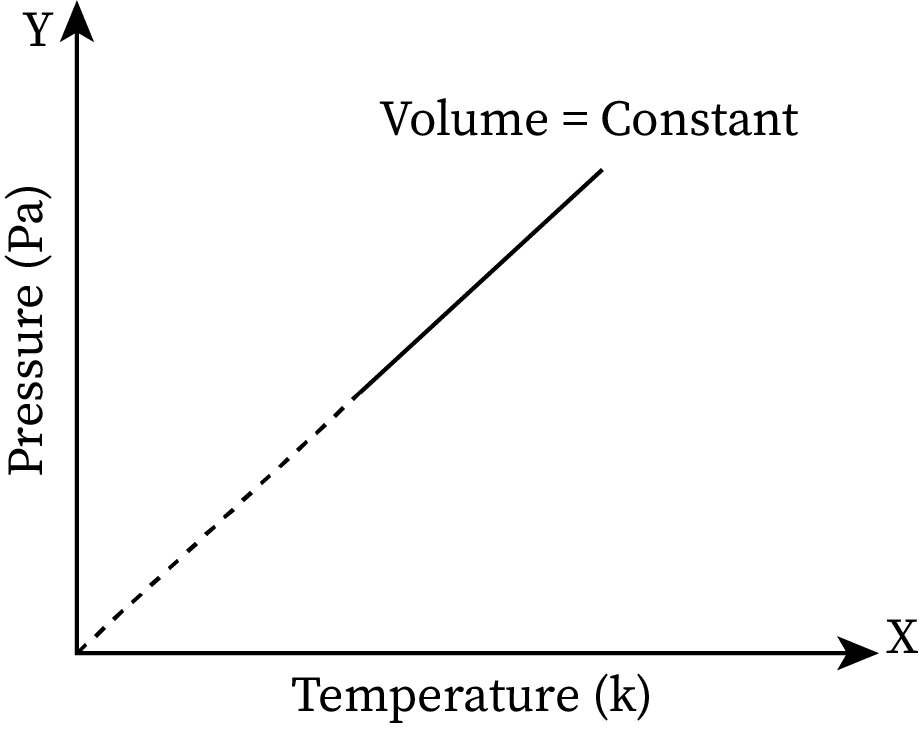
For all fluids, when the temperature increases, the velocity of the particles in the fluid also increases. When velocity increases, acceleration also increases. According to Newton’s second law of motion, acceleration is directly proportional to force (F=ma). Thus, when the force is increased, it causes an increase in pressure.
How pressure varies with volume?
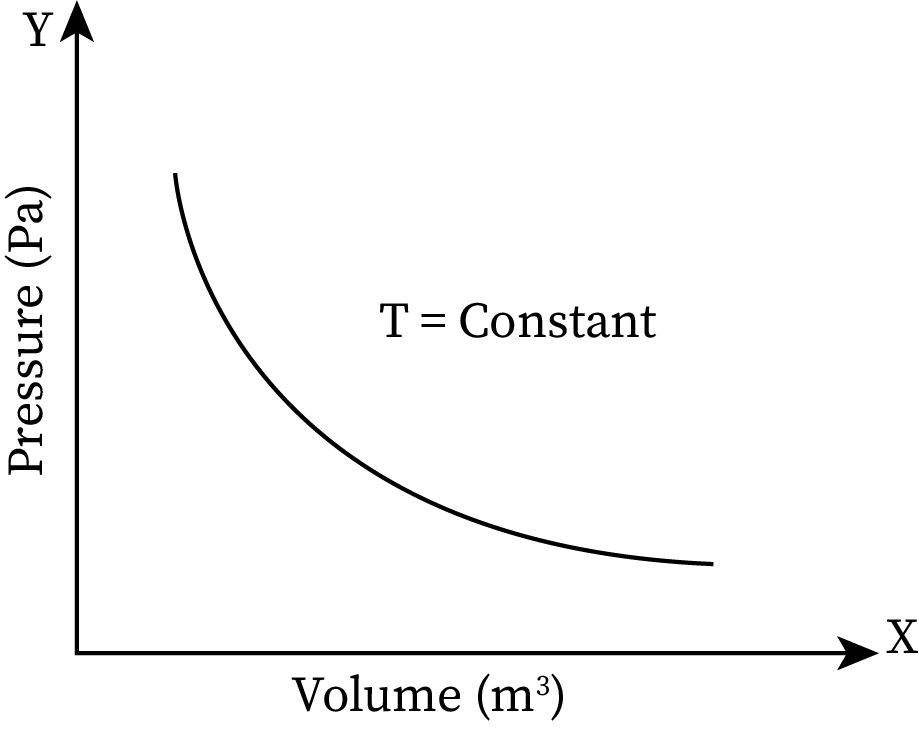
Boyle’s law states that at a constant temperature, the pressure exerted by a gas is inversely proportional to its volume. On increasing the volume of a gas, its pressure decreases, and vice versa.
The graphical representation of this relation is:
Variation of Blood pressure
Blood pressure is defined as the pressure exerted by the circulating blood on the walls of blood vessels or arteries. Since blood is also a fluid, all the factors affecting fluid pressure also affect the blood pressure. The short form used for blood pressure is BP, and the unit of blood pressure is millimeters of mercury (mm Hg).
The blood pressure is taken using two measurements—systolic and diastolic. Systolic blood pressure is measured when the heart beats and pressure have its highest value. Diastolic blood pressure is measured in the arteries between two adjacent heartbeats. The normal count for systolic pressure is less than 120 mm of Hg, and for diastolic pressure, it is less than 80 mm of Hg.
The main reasons for fluctuations in blood pressure are:
- Stress
- Activities such as exercise, talking, laughing, etc.
- Medical issues such as adrenal issues, white coat syndrome, blockage in blood vessels, etc.
- Certain foods and drinks
Common Mistakes
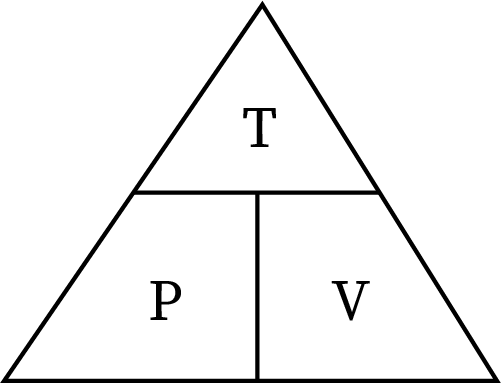
Mostly, students get confused between pressure-volume and pressure-temperature relationships. Pressure is directly proportional to temperature and inversely proportional to volume. The triangle relation between these three parameters helps to avoid confusion.
Context and Application
This topic is significant for professional exams for undergraduate and postgraduate courses, especially for,
Bachelor of Science in Physics
Bachelor of Science in Chemistry
Bachelor of Science in Botany
Bachelor of Science in Zoology
Bachelor of Science in Atmospheric Science
Master of Science in physics
Master of Science in Chemistry
Related Concepts
Boyle’s law
Amonton’s law
Fluid motion
Ideal gas equation
Newton’s law
Atmospheric pressure
Density
Acceleration due to gravity
Horizontal and Vertical forces
Practice Problems
Q.1 In the case of static fluid, pressure at the bottom of the vessel depends upon:
(a) Shape of the vessel
(b) Mass of the liquid
(c) Surface area of the base
(d) Height up to which liquid is filled inside the vessel
Correct option: (a)
Q.2 A liquid(densityρ) is filled up to a height H inside the vessel, then pressure at the bottom of the vessel is: (g is acceleration due to gravity)
(a) ρgh
(b) 2ρgh
(c) 3ρgh
(d) 4ρgh
Correct option: (a)
Q.3 A vessel is moving at a constant speed V towards right, how will pressure vary if we move from left to right along the horizontal axis?
(a) Pressure will decrease
(b) Pressure will increase
(c) Pressure will remain the same
(d) Cannot say
Correct option: (c)
Q.4 Pressure at the bottom of a lake is P. If pressure at the half depth is , then what is the depth of the lake? (Take atmospheric pressure as , acceleration due to gravity as g and density of water as )
(a)
(b)
(c)
(d)
Correct option: (d)
Q.5 Atmospheric pressure is equal to: (density of mercury, )
(a) 76 mm of Hg
(b) 760 mm of Hg
(c) 760 cm of Hg
(d) 7600 cm of Hg
Correct option: (b)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Variation of pressure Homework Questions from Fellow Students
Browse our recently answered Variation of pressure homework questions.