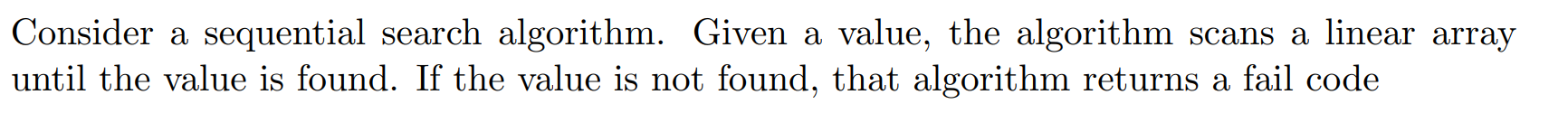
Consider a sequential search algorithm. Given a value, the algorithm scans a linear array until the value is found. If the value is not found, that algorithm returns a fail code (a) What is the best-case running time of this algorithm? Give the tightest asymptotic bound on the best-case running time using O notation. (b) What is the worst-base running time of this algorithm? Give the tightest asymptotic bound on the worst-case running time using O notation.

aolve algorithm Suppose that you are attending a one day conference in which several lectures are presented in parallel sessions e, more than one lecture may by running at the same timej. Lectures may be of different lengths. The lectures schedule is given to you in an array L such that Ld is the D of a lecture, L stort is the starting time of that lecture and Lend is the end time of that lecture. If you attend a lecture, you must atmtend it from the beginning until the end of it lyou are not allowed to amend lectures partialy. You want to amend as many lectures as possible. a) Give the pseudocode of an algorithm that takes as input the array Land finds the maximum number of lectures that you can attend. You can assume that dthe starting times and end times are integers representing time. The conterence sarts at time 0 and ends at some times. If you need to use a binary search algorithm or a sorting algorithm you can just calwithout gving s peudocode. fyou need to use any other…

Prime numbers can also be generated by an algorithm known as the Sieve of Eratosthenes . The algorithm for this procedure is presented here. Write a program that implements this algorithm so as to find all prime numbers up to n = 150. Sieve of Eratosthenes Algorithm To Display All Prime Numbers Between 1 and n Step 1: Define an array of integers P . Set all elements P i to 0, 2 <= i <= n. Step 2: Set i to 2. Step 3: If i > n , the algorithm terminates. Step 4: If P i is 0 (value i is a prime number), then i is prime and display its value. Step 5: For all positive integer values of j , such that i * j ≤ n , set P i ∗ j to 1 (non - prime). Step 6: Add 1 to i and go to step 3

If a linear search is performed on an array, and it is known that some items are searched for more frequently than others, how can the contents of the array be reordered to improve the average performance of the search?