
Floyd warshall
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

I have modified the code above. The input to test the method floydWarshal(graph,v) will come from the user (from the console through the scanner). v can not be a final variable because the user will determine the value of v. The double array graph will also be determined and input by the user (from the console through the scanner). I'm having issues getting the input from the user and putting it into the double array. I'm also having issues printing the result of the method, which should be the shortest path graph. Please help
------------------------------------------------------------------------------------
HERE IS THE CODE THAT I HAVE SO FAR
import java.io.*;
import java.util.*;
import java.lang.*;
public class Solution
{
final static int INF = 99999;
public static void shortWarshall(int graph[][],int v)
{
int dist[][] = new int[v][v];
int i, j, k;
/* Initialize the solution matrix
same as input graph matrix.
Or we can say the initial values
of shortest distances
are based on shortest paths
considering no intermediate
vertex. */
for (i = 0; i < v; i++)
for (j = 0; j < v; j++)
dist[i][j] = graph[i][j];
/* Add all vertices one by one
to the set of intermediate
vertices.
---> Before start of an iteration,
we have shortest
distances between all pairs
of vertices such that
the shortest distances consider
only the vertices in
set {0, 1, 2, .. k-1} as
intermediate vertices.
----> After the end of an iteration,
vertex no. k is added
to the set of intermediate
vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < v; k++) {
// Pick all vertices as source one by one
for (i = 0; i < v; i++) {
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < v; j++) {
// If vertex k is on the shortest path
// from i to j, then update the value of
// dist[i][j]
if (dist[i][k] + dist[k][j]
< dist[i][j])
dist[i][j]
= dist[i][k] + dist[k][j];
}
}
}
// Print the shortest distance matrix
// printSolution(dist);
for (int l = 0; l < v; ++l)
{
for (int m = 0; m < v; ++m)
{
if (dist[l][m] == INF)
System.out.print("INF ");
else
System.out.print(dist[l][m] + " ");
}
System.out.println();
}
}
/*public static void printSolution(int dist[][], int v)
{
for (int i = 0; i < v; ++i)
{
for (int j = 0; j < v; ++j)
{
if (dist[i][j] == INF)
System.out.print("INF ");
else
System.out.print(dist[i][j] + " ");
}
System.out.println();
}
}*/
public static void main(String[] args)
{
/* Enter your code here. Read input from STDIN. Print output to STDOUT. Your class should be named Solution. */
// Driver's code
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
Scanner scn = new Scanner(System.in);
int v = scn.nextInt();
int c = scn.nextInt();
int r = scn.nextInt();
int graph[][] = new int [c][r];
for(int i=0;i<c;i++)
{
for(int k=0;k<r;k++)
{
graph[i][k]=scn.nextInt();
}
}
// Function call
shortWarshall(graph,v);
}
}
------------------------------------------------------------------
I have also attached the error that I'm getting as a picture
Runtime Error
Error (stderr)
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: 0 at Solution.shortWarshall(Solution.java:24) at Solution.main(Solution.java:119
I have modified the code above. The input to test the method floydWarshal(graph,v) will come from the user (from the console through the scanner). v can not be a final variable because the user will determine the value of v. The double array graph will also be determined and input by the user (from the console through the scanner). I'm having issues getting the input from the user and putting it into the double array. I'm also having issues printing the result of the method, which should be the shortest path graph. Please help
------------------------------------------------------------------------------------
HERE IS THE CODE THAT I HAVE SO FAR
import java.io.*;
import java.util.*;
import java.lang.*;
public class Solution
{
final static int INF = 99999;
public static void shortWarshall(int graph[][],int v)
{
int dist[][] = new int[v][v];
int i, j, k;
/* Initialize the solution matrix
same as input graph matrix.
Or we can say the initial values
of shortest distances
are based on shortest paths
considering no intermediate
vertex. */
for (i = 0; i < v; i++)
for (j = 0; j < v; j++)
dist[i][j] = graph[i][j];
/* Add all vertices one by one
to the set of intermediate
vertices.
---> Before start of an iteration,
we have shortest
distances between all pairs
of vertices such that
the shortest distances consider
only the vertices in
set {0, 1, 2, .. k-1} as
intermediate vertices.
----> After the end of an iteration,
vertex no. k is added
to the set of intermediate
vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < v; k++) {
// Pick all vertices as source one by one
for (i = 0; i < v; i++) {
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < v; j++) {
// If vertex k is on the shortest path
// from i to j, then update the value of
// dist[i][j]
if (dist[i][k] + dist[k][j]
< dist[i][j])
dist[i][j]
= dist[i][k] + dist[k][j];
}
}
}
// Print the shortest distance matrix
// printSolution(dist);
for (int l = 0; l < v; ++l)
{
for (int m = 0; m < v; ++m)
{
if (dist[l][m] == INF)
System.out.print("INF ");
else
System.out.print(dist[l][m] + " ");
}
System.out.println();
}
}
/*public static void printSolution(int dist[][], int v)
{
for (int i = 0; i < v; ++i)
{
for (int j = 0; j < v; ++j)
{
if (dist[i][j] == INF)
System.out.print("INF ");
else
System.out.print(dist[i][j] + " ");
}
System.out.println();
}
}*/
public static void main(String[] args)
{
/* Enter your code here. Read input from STDIN. Print output to STDOUT. Your class should be named Solution. */
// Driver's code
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
Scanner scn = new Scanner(System.in);
int v = scn.nextInt();
int c = scn.nextInt();
int r = scn.nextInt();
int graph[][] = new int [c][r];
for(int i=0;i<c;i++)
{
for(int k=0;k<r;k++)
{
graph[i][k]=scn.nextInt();
}
}
// Function call
shortWarshall(graph,v);
}
}
------------------------------------------------------------------
I have also attached the error that I'm getting as a picture
Runtime Error
Error (stderr)
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: 0 at Solution.shortWarshall(Solution.java:24) at Solution.main(Solution.java:119

- max edge distance Simplification key Figure 4-1: A sample process for the Douglas-Peucker algorithm The Douglas-Peucker algorithm is for the selection of representative points to simplify a curve composed of line segments. It uses a point-to-edge distance tolerance. The algorithm starts with a crude simplification that is the single edge joining the first and last vertices of the original polyline. It then computes the perpendicular distance of all intermediate vertices to that edge. The vertex that is furthest away from that edge, and that has a computed distance that is larger than a specified tolerance, will be marked as a key and added to the simplification. This process will recurse for each edge in the current simplification until all vertices of the original polyline are within tolerance of the simplification results. This process is illustrated in Figure 4-1. (1) Given three points (xp, Yp), (Xa, Ya), (Xp,Yb), show a detailed process to compute the perpendicular distance from p…arrow_forwardc) Find a Hamiltonian Cycle starting at vertex A. Draw the Hamiltonian Cycle on the graph and list the vertices of the cycle. K L M A B E F G H J Note: A Hamiltonian Cycle is a simple cycle that traverses all vertices. A simple cycle starts at a vertex, visits other vertices once then returns to the starting vertex. For instance, if the vertices of Ks were labeled A, B, C, D, E, one Hamiltonian Cycle would be ABCDEA.arrow_forwardImplement this solution in Javaarrow_forward
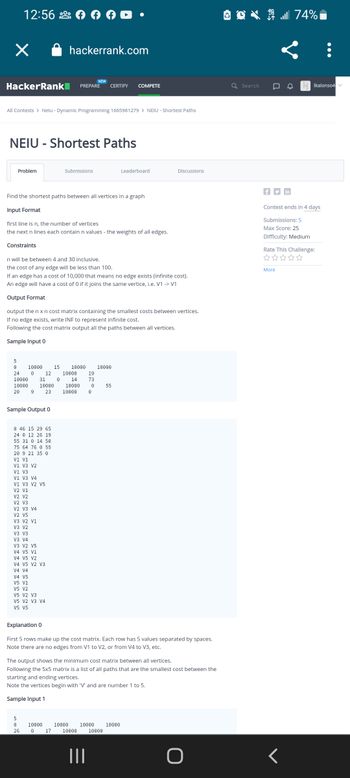
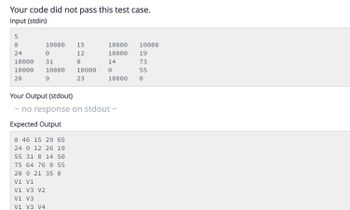
- Discrete math: (a) Apply improved Dijkstra’s algorithm to the following graph to find the shortest path from A to every other vertex in the graph. (b) Apply Kruskal’s algorithm to the graph to find a minimum spanning tree.arrow_forwardFind the number of connected components for the following graph.arrow_forwardUsing Dijkstra’s algorithm, find the shortest path between C and all other vertices. Write the python algorithm for it.arrow_forward
- Write a Java program for Dijkstra’s algorithm for the shortest path. Input Vertices and Edges from user and Find the shortest path from the first node as the source to all other nodes as destinations. Run the program and display output samplesarrow_forwardJava programming Computer science Please please help me Im desperate for your help please? I dont understand this that well. Pleasearrow_forwardSuppose you have a graph with 100 nodes and 500 edges and you want to find the shortest path between two nodes using Dijkstra's algorithm. What is the time complexity of this operation?arrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





