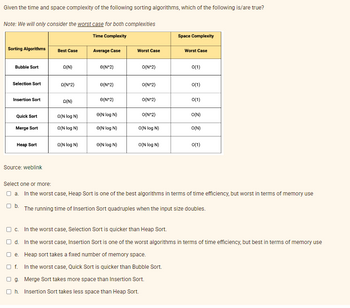
Given the time and space complexity of the following sorting algorithms, which of the following is/are true? Note: We will only consider the worst case for both complexities Time Complexity Average Case Sorting Algorithms Bubble Sort Selection Sort Insertion Sort Quick Sort Merge Sort Heap Sort Best Case Q(N) Q(N^2) Q(N) O(N log N) Q(N log N) Q(N log N) e(N^2) 0(N^2) (N^2) (N log N) (N log N) O(N log N) Worst Case O(N^2) O(N^2) O(N^2) O(N^2) O(N log N) O(N log N) Space Complexity Worst Case 0(1) 0(1) 0(1) O(N) O(N) 0(1) Source: weblink Select one or more: a. In the worst case, Heap Sort is one of the best algorithms in terms of time efficiency, but worst in terms of memory use b. The running time of Insertion Sort quadruples when the input size doubles. c. In the worst case, Selection Sort is quicker than Heap Sort. d. In the worst case, Insertion Sort is one of the worst algorithms in terms of time efficiency, but best in terms of memory use e. Heap sort takes a fixed number of memory space. Of. In the worst case, Quick Sort is quicker than Bubble Sort. g. Merge Sort takes more space than Insertion Sort. h. Insertion Sort takes less space than Heap Sort.

Show that the following statement is true: No compare-based sorting algorithm can ensure that N items will be sorted with less than lg(N!) N lg N comparisons.

The worst-time complexity for merge sort is O(1) O O(log2N) O O(N) O(NlogN) O O(N*N)

Is searching with pre-sorting usually worse or better than sequential search in time complexity? [Select] Which is more useful in practice since we usually do more lookups after a one-time sorting? [Select] What kind of search do we apply for its efficiency? [Select] [Select] binary search decimal search How much time does it take for the worst case whe [Select]

Comparison of the time complexity among different sorting algorithms ? (multiple choice) ^: Indicates exponent operation 單選或多選: ☐a. Worst case of Radix sort is O(n^2) Ob. Best case of Bubble sort is O(n^2) c. Worst case of Quick sort is O(n^2) Od. Best case of Selection sort is O(n^2) ☐e. Best case of Radix sort is O(nlogn) f. Average case of Shell sort is O(n) Og. Worst case of Merge sort is O(nlogn) Oh. Best case of Quick sort is O(n) ☐i. Average case of Insertion sort is O(n^2) O j. Average case of Quick sort is O(n^2) Ok. Average case of Merge sort is O(nlogn) O 1. Worst case of Selection sort is O(n^2)

You are given two sorted arrays  A = [1, 2, 3] B = [2, 5, 6, 7], o/p = [1, 2, 2, 3, 5, 6, 7] Write an algorithm to merge these sorted arrays. Mention the time and space complexity of your algorithm

What is the run time efficiency of an insertion algorithm?a) O(N)b) O(log N)c) O(N2)d) O(M log N)