
JavaScript: Search the Tree
A binary search tree is a data structure that consists of JavaScript objects called "nodes". A tree always has a root node which holds its own integer valueproperty and can have up to two child nodes (or leaf nodes), a left and right attribute. A leaf node holds a value attribute and, likewise, a left and rightattribute each potentially pointing to another node in the binary tree. Think of it as a Javascript object with potentially more sub-objects referenced by the left and right attributes (as seen in assignment 4). There are certain rules that apply to a binary tree:
- A node's left leaf node has a value that is <= than to its own value
- A node's right leaf node has a value that is => its own value
In other words:
let node = {
value: <some number>
left: <a node object with value attribute <= this object's value>
right: <a node object with value attribute >= this object's value>
}
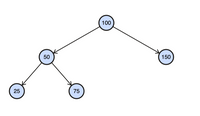
If you need a visual aid, below is an example of what a binary tree looks like according to the above rules: -- image attached.
You will be writing a function called isPresent that takes two arguments: the root object and a value (number), and returns a boolean: true if the value is present in the tree or false if it is not present.
function isPresent(root, value) {
// your code here
// return boolean
}
Let's translate the above image into a familiar JavaScript object below as an example:
let tree = {
"value": 100,
"left": {
"value": 50,
"left": {
"value": 25,
"left": null,
"right": null
},
"right": {
"value": 75,
"left": null,
"right": null
}
},
"right": {
"value": 150,
"left": null
"right": null
}
}
console.log(isPresent(tree, 25))
Output: true
Reasoning: 25 is the value of a leaf node in the binary tree
..
"left": {
"value": 25,
"left": null,
"right": null
},
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

- Javaarrow_forwardJava code that eliminates the binary search's node with the lowest value. returns a reference to its element from a tree. If this tree is empty, it raises an EmptyCollectionException. If the tree is empty, returning a reference to the node with the fewest values produces an EmptyCollectionException.arrow_forward1. Create a Java program that prompts the user the initial choices for the Binary Search Treea. User chooses 1: Insert, User chooses 2: Delete, User chooses 3: Show BinaryTree, User chooses 4: Exit Program 2. Insertion in a tree should be such that it obeys the main properties of the binary searchtree. The basic algorithm should be:a. If the node to be inserted is greater than the existing root, move down a levelthrough the right pointer of the root.b. If the node to be inserted is lesser than the existing root, move down a levelthrough the left pointer of the root.c. Repeat this process for all nodes till the leaves are reached.d. Insert the node as the left or right pointer for the leaf (based on its value - if it issmaller than the leaf, it should be inserted as the left pointer; if it is larger than theleaf, it should be inserted as the right pointer) 3. Deletion is a bit more complicated than insertion because it varies depending on the nodethat needs to be deleted from the…arrow_forward
- Explore the concept of Binary Expression Trees and their role in evaluating mathematical expressions. How can you construct and evaluate expressions using binary expression trees?arrow_forwardJAVA Create binary search tree shown as below. Now delete the key 18, and then calculate the balance factor and convert into AVLtree by proper rotationarrow_forwardAlert dont submit AI generated answer. Define a Binary Search Tree. Explain the advantage of a Binary Search Tree data structure. Create a Binary Search Tree (visually the way we did in the class) on the following input data. Show the status of the values during each step. NOTE: You have to describe the condition(s) used and the steps justifying the task of placing the value at a location. 34, 21, 43, 19, 20, 39, 19, 52arrow_forward
- HTML may be used to build apps that demonstrate how to use the Search Tree Structures concept. These applications may be used to demonstrate how the representation works.arrow_forward12:34 A cs61a.org Implement add_d_leaves, a function that takes in a Tree instance t and a number v. We define the depth of a node in t to be the number of edges from the root to that node. The depth of root is therefore 0. For each node in the tree, you should add d leaves to it, where d is the depth of the node. Every added leaf should have a label of v. If the node at this depth has existing branches, you should add these leaves to the end of that list of branches. For example, you should be adding 1 leaf with label v to each node at depth 1, 2 leaves to each node at depth 2, and so on. Here is an example of a tree t (shown on the left) and the result after add_d_leaves is applied with v as 5. 3 2 3 2 4 4 5 5 5 Hint: Use a helper function to keep track of the depth! def add_d_leaves(t, v): """Add d leaves containing v to each ngarrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





