Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Related questions
Question
(b) Source Code
Write solution in Phython
Code should be well written and commented.
![Problem 1 Is Graph Bipartite?
There is an undirected graph with n nodes, where each node is numbered between 0 and n- 1.
You are given a 2D array graph, where graphlu] is an array of nodes that node u is adjacent to.
More formally, for each v in graphlu), there is an undirected edge between node u and node v.
The graph has the following properties:
• There are no self-edges (graphlu] does not contain u).
There are no parallel edges (graphlu] does not contain duplicate values).
• If v is in graph[u), then u is in graph[u} (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there
is no path between them.
A graph is bipartite if the nodes can be partitioned into two disjoint sets A and B such that
every edge in the graph connects a node in set A and a node in set B.
There are other equivalent definitions of a bipartite graph. A graph is bipartite if and only if it has
no odd length cycle, i.e., no cycle in the graph has an odd mumber of edges. Note that if a graph has no
cycles it is bipartite (hence trees are bipartite graphs).
It is an interesting exercise for you to show that the above two definitions are equivalent (highly
recommended if you want to get a taste of graph theory). But that is not the goal of this exercise.
Using the odd cycle definition one can use DFS or BFS to elegantly check whether a graph is bipartite
in linear time, ie., O(m + n) time. Such solutions are discussed in leetcode (note that some of these may
not be fully correct). This is also not the goal of this exercise.
accepted and will receive O points.
The goal of this exercise is to explore yet another approach to check bipartiteness and is based on the
following ides. You have to argue that the idea is correct (as mentioned below) and implement the idea
as an algorithm that checks for bipartiteness of a graph.
Let G = (V,E) be the input graph that you want to check for bipartiteness. We first transform G
into a new graph G' = (V', E') as follows. For each esch node v e V, construct two nodes v1, v2 € V'
and for each edge (u, v) € E, create two edges (u1, 12) and (u2, v1) in E'. This completes the description
of constructing G' from G. See Figure 1 for an illustration.
The idea of this construction is that we reduce the problem of checking bipartiteness of G to checking
the number of connected components of G as stated in the following theorem.
you give such a solution, this will not be
Theorem 1
Let C be the mumber of connected components in G. Then the mumber of connected components
in G' is 20 if and only if the graph G is bipartite.
Your first goal is to give a proof of the above theorem (soe the submissions instruetions below).
To get an idea of why the above theorem might be true, see the two examples given in Figures 1
and 2. The graph in Example 1 is bipartite (no cycle) and the number of connected components is 1; it is
2 in G'. The graph in Example 2 is not bipartite (odd cycle of length 3) and the number of connected
components is 1; it is 1 also in G'.
Your second goal is to use the theorem above to give an efficient algorithm for checking bipartiteness.](https://content.bartleby.com/qna-images/question/646a794d-e587-473e-a1b8-2a8879d17700/31b05bf7-d05e-4eed-8eb3-c95c6d9b93fc/7awc6ld_processed.jpeg)
Transcribed Image Text:Problem 1 Is Graph Bipartite?
There is an undirected graph with n nodes, where each node is numbered between 0 and n- 1.
You are given a 2D array graph, where graphlu] is an array of nodes that node u is adjacent to.
More formally, for each v in graphlu), there is an undirected edge between node u and node v.
The graph has the following properties:
• There are no self-edges (graphlu] does not contain u).
There are no parallel edges (graphlu] does not contain duplicate values).
• If v is in graph[u), then u is in graph[u} (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there
is no path between them.
A graph is bipartite if the nodes can be partitioned into two disjoint sets A and B such that
every edge in the graph connects a node in set A and a node in set B.
There are other equivalent definitions of a bipartite graph. A graph is bipartite if and only if it has
no odd length cycle, i.e., no cycle in the graph has an odd mumber of edges. Note that if a graph has no
cycles it is bipartite (hence trees are bipartite graphs).
It is an interesting exercise for you to show that the above two definitions are equivalent (highly
recommended if you want to get a taste of graph theory). But that is not the goal of this exercise.
Using the odd cycle definition one can use DFS or BFS to elegantly check whether a graph is bipartite
in linear time, ie., O(m + n) time. Such solutions are discussed in leetcode (note that some of these may
not be fully correct). This is also not the goal of this exercise.
accepted and will receive O points.
The goal of this exercise is to explore yet another approach to check bipartiteness and is based on the
following ides. You have to argue that the idea is correct (as mentioned below) and implement the idea
as an algorithm that checks for bipartiteness of a graph.
Let G = (V,E) be the input graph that you want to check for bipartiteness. We first transform G
into a new graph G' = (V', E') as follows. For each esch node v e V, construct two nodes v1, v2 € V'
and for each edge (u, v) € E, create two edges (u1, 12) and (u2, v1) in E'. This completes the description
of constructing G' from G. See Figure 1 for an illustration.
The idea of this construction is that we reduce the problem of checking bipartiteness of G to checking
the number of connected components of G as stated in the following theorem.
you give such a solution, this will not be
Theorem 1
Let C be the mumber of connected components in G. Then the mumber of connected components
in G' is 20 if and only if the graph G is bipartite.
Your first goal is to give a proof of the above theorem (soe the submissions instruetions below).
To get an idea of why the above theorem might be true, see the two examples given in Figures 1
and 2. The graph in Example 1 is bipartite (no cycle) and the number of connected components is 1; it is
2 in G'. The graph in Example 2 is not bipartite (odd cycle of length 3) and the number of connected
components is 1; it is 1 also in G'.
Your second goal is to use the theorem above to give an efficient algorithm for checking bipartiteness.
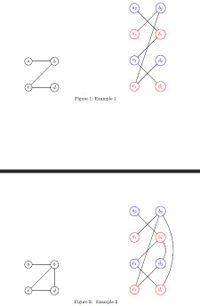
Transcribed Image Text:b
da
di
Figure 1: Example 1
b2
da
Figure 2: Example 2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- 2. This question is about code generation. (a) What data structure is used as input to code generators? What feature of it makes the implementation of code generators simple and efficient?arrow_forwardVocabulary Task (C language) Natural language processing (NLP) is a field of artificial intelligence that seeks to develop the ability of a computer program to understand human language. Usually, the first step of an NLP system is to convert words into numeric codes. Thus, the system converts an input text into a sequence of numeric codes before any high-level analysis. This process is known as text preprocessing. We can only perform text preprocessing if we have a vocabulary of words and their associated numeric codes. Your task is to create a vocabulary of unique words for a given text file and assign a different number from 1 to N to each unique word, with N being the total number of unique words. You must perform this assignment so that the first word in alphabetical order gets the number 1, the second word in alphabetical order gets the number 2, and so on. A word is a sequence of letters (uppercase or lowercase). The file is composed of letters and white spaces (spaces, tabs,…arrow_forwardThis article discusses bool data types and logical expressions.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON 
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education
Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON
Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON
C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON
Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning
Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education