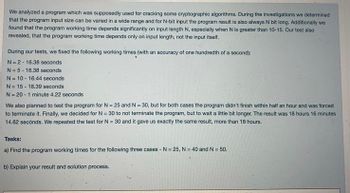
We analyzed a program which was supposedly used for cracking some cryptographic algorithms. During the investigations we determined that the program input size can be varied in a wide range and for N-bit input the program result is also always N bit long. Additionally we found that the program working time depends significantly on input length N, especially when N is greater than 10-15. Our test also revealed, that the program working time depends only on input length, not the input itself. During our tests, we fixed the following working times (with an accuracy of one hundredth of a second): N=2-16.38 seconds N= 5-16.38 seconds N 10-16.44 seconds N=15-18.39 seconds N=20-1 minute 4.22 seconds We also planned to test the program for N=25 and N= 30, but for both cases the program didn't finish within half an hour and was forced to terminate it. Finally, we decided for N= 30 to not terminate the program, but to wait a little bit longer. The result was 18 hours 16 minutes 14.62 seconds. We repeated the test for N= 30 and it gave us exactly the same result, more than 18 hours. Tasks: a) Find the program working times for the following three cases - N=25, N = 40 and N = 50. b) Explain your result and solution process.

Implement Tower of Hanoi algorithm in your preferred programming language. Then run the implementation with 1, 5, 25, and 125 disks. Record the amount of time it takes for each of these input sizes. What do you infer from this experiment?

Implementing matrix addition is pretty simple; see the program below. However, the given addition function matrix_add_double() does not run at full speed.  On the instructors computer, which has 16GB of RAM, the program below shows that the call to matrix_add_double takes 38571 ms, while another, better implementation achieves the same result in 3794.7ms, which is 10.2 times faster! Your job for this exercise is:          • to explain what in the Operating System and/or CPU and/or other part of the system makes the implementation              below go so slowly.          • to fix the code to achieve full speed. Hint: There are two reasons why the code runs slowly. The one reason is related to how virtual addresses get translated to physical addresses, the other reasons is related to another effect in the hardware. Only the performance for the matrix_add_double function() counts for your exam results. You can leave the other parts of the code untouched, but you may also change them.…

An algorithm that takes 2(n) time ( always / sometimes / never ) takes more time to run than an algorithm that takes w(n) time on the same input and hardware, where n is the length of the input. sometimes never always