
The normal frequencies of small oscillations and describe the motion of the oscillation in corresponding normal modes.
Answer to Problem 11.26P
The normal frequencies of small oscillations of the beads are
Explanation of Solution
Write the Lagrangian of the system
Here,
Write the Lagrangian equation of motion, if the Lagrangian of the system is function of
Write the moment of inertia of the system from parallel axis theorem
Here,
The mass of the hoop is
Substitute equation (IV) in (III) and solve for
Write the equation to find the kinetic energy of the hoop
Substitute
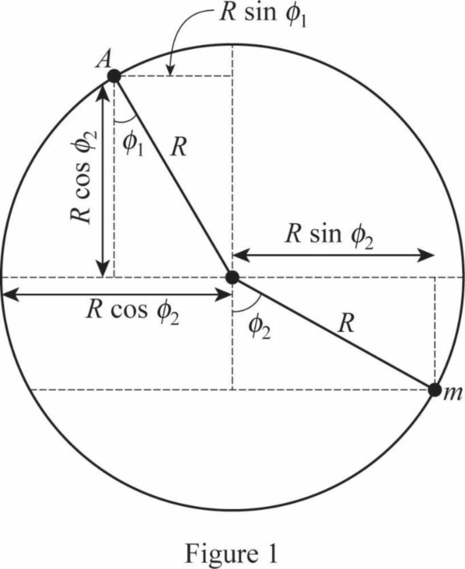
In Figure,
Consider
Hence, the position of the bead can be expressed as
Differentiate the above equation to find the velocity of the bead
Consider
Write the equation to find the kinetic energy of bead
Here,
Substitute equation (VI) in the above equation to solve for
Since
Write the formula to find the total kinetic energy of the system
Substitute equation (V) and (VII) in the above equation and solve for
About the point
Write the equation for the potential energy of hoop
Here,
Substitute the expression of
Ignoring the higher terms the above equation becomes,
Form figure, the vertical component of position of the bead is
Write the equation for the potential energy of bead
Substitute the expression of
Ignoring the higher terms the above equation becomes,
In the above equation,
The above equation becomes,
Write the formula to find the total potential energy of the system
Substitute (IX) and (X) in the above equation to solve for
Substitute (VIII) and (XI) in equation (I)
Write the expression of Lagrangian equations of motion in term of
Substitute (XII) in the above equation and solve
Dividing
Write the expression of Lagrangian equations of motion in term of
Substitute (XII) in the above equation and solve
Dividing
The equation of the motion of the mass along
Write the general equation of motion
Comparing the above equation of motion with the general equation of the motion
If the frequency
Substitute the matrices in the above equation
The determinant of
Factorize the above expression and solving,
Hence,
And
Therefore, the normal frequency for the small oscillation of the beads are
First normal mode for the normal frequency is
Substitute
The eigenvalue of the equation becomes
The equation becomes,
And,
Solving the above equation gives,
These implies equation can be written in the form of
Therefore, the complex column
The real form of
Thus, the first normal mode is
Second normal mode for the normal frequency is
Substitute
The eigenvalue of the equation becomes
The equation becomes,
And,
Solving the above equation gives,
These implies equation can be written in the form of
Therefore, the complex column
The real form of
Thus, the second normal mode is
Conclusion:
The normal frequencies of small oscillations of the beads are
Want to see more full solutions like this?
Chapter 11 Solutions
Classical Mechanics
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





