
Calculus
10th Edition
ISBN: 9781285057095
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Chapter 12, Problem 3PS
To determine
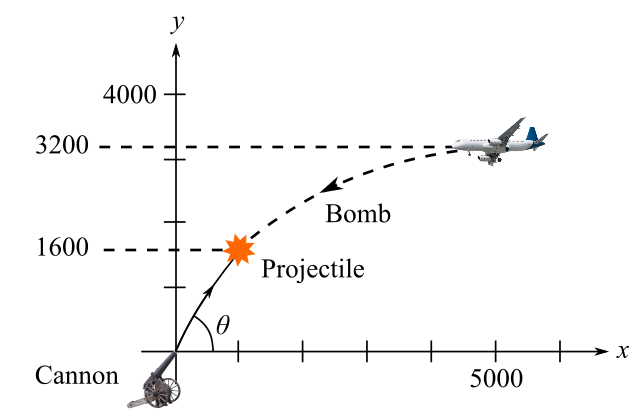
To calculate: The required initial speed and angle of inclination of projectilethat intercepts the bomb at an altitude of
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 12 Solutions
Calculus
Ch. 12.1 - Finding the Domain In exercises 310 find the...Ch. 12.1 - Finding the domain In exercises 310 find the...Ch. 12.1 - Prob. 3ECh. 12.1 - Finding the domain In exercises 3-10 find the...Ch. 12.1 - Prob. 5ECh. 12.1 - Prob. 6ECh. 12.1 - Finding the domain In exercises 310 find the...Ch. 12.1 - Prob. 8ECh. 12.1 - Prob. 9ECh. 12.1 - Evaluating a function In Exercises 11 and 12...
Ch. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - Writing a Vector-Valued FunctionIn Exercises 1316,...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Prob. 19ECh. 12.1 - Prob. 20ECh. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Prob. 23ECh. 12.1 - Prob. 24ECh. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.1 - Prob. 33ECh. 12.1 - Prob. 34ECh. 12.1 - Prob. 35ECh. 12.1 - Prob. 36ECh. 12.1 - Prob. 37ECh. 12.1 - Prob. 38ECh. 12.1 - Prob. 39ECh. 12.1 - Prob. 42ECh. 12.1 - Prob. 41ECh. 12.1 - Prob. 40ECh. 12.1 - Prob. 43ECh. 12.1 - Transformations of Vector-Valued Functions In...Ch. 12.1 - Prob. 45ECh. 12.1 - Prob. 46ECh. 12.1 - Representing a Graph by a Vector-Valued Function...Ch. 12.1 - Prob. 48ECh. 12.1 - Prob. 49ECh. 12.1 - Prob. 50ECh. 12.1 - Prob. 51ECh. 12.1 - Prob. 52ECh. 12.1 - Representing a Graph by Vector-Valued Function In...Ch. 12.1 - Prob. 54ECh. 12.1 - Prob. 55ECh. 12.1 - Prob. 56ECh. 12.1 - Prob. 57ECh. 12.1 - Prob. 58ECh. 12.1 - Prob. 59ECh. 12.1 - Prob. 60ECh. 12.1 - Prob. 61ECh. 12.1 - Prob. 62ECh. 12.1 - Prob. 63ECh. 12.1 - Prob. 64ECh. 12.1 - Prob. 65ECh. 12.1 - Prob. 66ECh. 12.1 - Prob. 67ECh. 12.1 - Prob. 68ECh. 12.1 - Prob. 69ECh. 12.1 - Prob. 70ECh. 12.1 - Prob. 71ECh. 12.1 - Prob. 72ECh. 12.1 - Prob. 73ECh. 12.1 - Prob. 74ECh. 12.1 - Prob. 75ECh. 12.1 - Prob. 76ECh. 12.1 - Prob. 77ECh. 12.1 - Prob. 78ECh. 12.1 - Prob. 79ECh. 12.1 - Prob. 80ECh. 12.1 - Prob. 81ECh. 12.1 - HOW DO YOU SEE IT? The four figures below are...Ch. 12.1 - Prob. 83ECh. 12.1 - Prob. 84ECh. 12.1 - Prob. 85ECh. 12.1 - Prob. 86ECh. 12.1 - Prob. 87ECh. 12.1 - Prob. 88ECh. 12.1 - Prob. 89ECh. 12.1 - Prob. 90ECh. 12.1 - Prob. 91ECh. 12.1 - Prob. 92ECh. 12.1 - Prob. 93ECh. 12.1 - Prob. 94ECh. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Finding a Derivative In Exercises 9–20, find...Ch. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - Prob. 19ECh. 12.2 - Finding a Derivative In Exercises 11-18, find...Ch. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Higher-Order DifferentiationIn Exercises 1922,...Ch. 12.2 - Prob. 24ECh. 12.2 - Prob. 25ECh. 12.2 - Prob. 26ECh. 12.2 - Prob. 27ECh. 12.2 - Prob. 28ECh. 12.2 - Prob. 29ECh. 12.2 - Prob. 30ECh. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Prob. 32ECh. 12.2 - Prob. 33ECh. 12.2 - Prob. 34ECh. 12.2 - Prob. 35ECh. 12.2 - Prob. 36ECh. 12.2 - Prob. 37ECh. 12.2 - Prob. 38ECh. 12.2 - Using Properties of the Derivative In Exercises 35...Ch. 12.2 - Using Properties of the DerivativeIn Exercises 35...Ch. 12.2 - Using Two MethodsIn Exercises 37 and 38, find (a)...Ch. 12.2 - Prob. 42ECh. 12.2 - Prob. 43ECh. 12.2 - Prob. 44ECh. 12.2 - Prob. 45ECh. 12.2 - Prob. 46ECh. 12.2 - Prob. 47ECh. 12.2 - Prob. 49ECh. 12.2 - Prob. 48ECh. 12.2 - Finding an Indefinite Integral In Exercises 39-46,...Ch. 12.2 - Prob. 51ECh. 12.2 - Evaluating a Definite Integral In Exercises 47-52,...Ch. 12.2 - Prob. 53ECh. 12.2 - Prob. 54ECh. 12.2 - Evaluating a Definite Integral In Exercises 47-52,...Ch. 12.2 - Prob. 56ECh. 12.2 - Prob. 57ECh. 12.2 - Prob. 58ECh. 12.2 - Prob. 59ECh. 12.2 - Prob. 60ECh. 12.2 - Prob. 61ECh. 12.2 - Finding an Antiderivative In Exercises 53-58, find...Ch. 12.2 - Prob. 65ECh. 12.2 - Prob. 64ECh. 12.2 - 63. Differentiation State the definition of the...Ch. 12.2 - Prob. 66ECh. 12.2 - Prob. 67ECh. 12.2 - Prob. 68ECh. 12.2 - Prob. 69ECh. 12.2 - Prob. 70ECh. 12.2 - Prob. 71ECh. 12.2 - Prob. 72ECh. 12.2 - Prob. 73ECh. 12.2 - Prob. 74ECh. 12.2 - Particle MotionA particle moves in the xy-plane...Ch. 12.2 - Particle MotionA particle moves in the yz-plane...Ch. 12.2 - Prob. 77ECh. 12.2 - Prob. 78ECh. 12.2 - Prob. 79ECh. 12.2 - True or False? In Exercises 73-76, determine...Ch. 12.2 - Prob. 81ECh. 12.2 - Prob. 82ECh. 12.3 - Prob. 1ECh. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Finding Velocity and Acceleration Vectors in Space...Ch. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.3 - Prob. 19ECh. 12.3 - Prob. 20ECh. 12.3 - Prob. 21ECh. 12.3 - Prob. 22ECh. 12.3 - Prob. 23ECh. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - A baseball player at second base throws a ball 90...Ch. 12.3 - Prob. 29ECh. 12.3 - Prob. 30ECh. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - A bomber is flying horizontally at an altitude of...Ch. 12.3 - Prob. 35ECh. 12.3 - Prob. 36ECh. 12.3 - Prob. 37ECh. 12.3 - Prob. 38ECh. 12.3 - Projectile Motion In Exercises 41 and 42, use the...Ch. 12.3 - Prob. 40ECh. 12.3 - Prob. 41ECh. 12.3 - Prob. 42ECh. 12.3 - Prob. 43ECh. 12.3 - Prob. 44ECh. 12.3 - Prob. 45ECh. 12.3 - Prob. 46ECh. 12.3 - Prob. 47ECh. 12.3 - Prob. 48ECh. 12.3 - 57095-12.3-49E-Question-Digital.docx Circular...Ch. 12.3 - Prob. 50ECh. 12.3 - Prob. 51ECh. 12.3 - Prob. 52ECh. 12.3 - Prob. 53ECh. 12.3 - Prob. 54ECh. 12.3 - Particle Motion Consider a particle moving on an...Ch. 12.3 - Prob. 57ECh. 12.3 - Prob. 55ECh. 12.3 - Prob. 58ECh. 12.3 - Prob. 59ECh. 12.3 - Prob. 60ECh. 12.3 - Prob. 61ECh. 12.3 - Prob. 62ECh. 12.4 - Prob. 44ECh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - Finding the Unit Tangent Vector In Exercises 3-8,...Ch. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - Prob. 26ECh. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Finding Vectors In Exercises 37–42, find T(t),...Ch. 12.4 - Prob. 43ECh. 12.4 - Prob. 45ECh. 12.4 - Prob. 46ECh. 12.4 - Prob. 47ECh. 12.4 - Prob. 48ECh. 12.4 - Cycloidal Motion The figure shows the path of a...Ch. 12.4 - Motion Along an Involute of a Circle The figure...Ch. 12.4 - Prob. 51ECh. 12.4 - Prob. 52ECh. 12.4 - Prob. 53ECh. 12.4 - Prob. 54ECh. 12.4 - Prob. 55ECh. 12.4 - Prob. 56ECh. 12.4 - Prob. 57ECh. 12.4 - Prob. 58ECh. 12.4 - Prob. 59ECh. 12.4 - Prob. 60ECh. 12.4 - Projectile Motion Find the tangential and normal...Ch. 12.4 - Prob. 62ECh. 12.4 - Prob. 63ECh. 12.4 - Prob. 64ECh. 12.4 - Air Traffic ControlBecause of a storm, ground...Ch. 12.4 - Projectile Motion A plane flying at an altitude of...Ch. 12.4 - Prob. 67ECh. 12.4 - Prob. 68ECh. 12.4 - Prob. 69ECh. 12.4 - Prob. 70ECh. 12.4 - Prob. 71ECh. 12.4 - Prob. 72ECh. 12.4 - Prob. 73ECh. 12.4 - Prob. 74ECh. 12.4 - Prob. 75ECh. 12.4 - Proof Prove that the principal unit normal vector...Ch. 12.4 - Prob. 77ECh. 12.4 - Prob. 78ECh. 12.4 - Prob. 79ECh. 12.4 - Prob. 80ECh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - 57095-12.5-7E-Question-Digital.docx Projectile...Ch. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Investigation Consider the helix represented by...Ch. 12.5 - Prob. 16ECh. 12.5 - Prob. 18ECh. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Finding Curvature In Exercises 19–22, find the...Ch. 12.5 - Prob. 22ECh. 12.5 - Prob. 23ECh. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - Prob. 26ECh. 12.5 - Prob. 27ECh. 12.5 - Prob. 28ECh. 12.5 - Finding CurvatureIn Exercises 2936, find the...Ch. 12.5 - Prob. 30ECh. 12.5 - Prob. 31ECh. 12.5 - Prob. 32ECh. 12.5 - Prob. 33ECh. 12.5 - Prob. 34ECh. 12.5 - Prob. 35ECh. 12.5 - Prob. 36ECh. 12.5 - Prob. 37ECh. 12.5 - Prob. 38ECh. 12.5 - Prob. 39ECh. 12.5 - Prob. 40ECh. 12.5 - Prob. 41ECh. 12.5 - Prob. 42ECh. 12.5 - Finding Curvature in Rectangular Coordinates In...Ch. 12.5 - Prob. 44ECh. 12.5 - Prob. 45ECh. 12.5 - Prob. 46ECh. 12.5 - Prob. 47ECh. 12.5 - Prob. 48ECh. 12.5 - Prob. 49ECh. 12.5 - Prob. 50ECh. 12.5 - Prob. 51ECh. 12.5 - Prob. 52ECh. 12.5 - Prob. 53ECh. 12.5 - Prob. 54ECh. 12.5 - Prob. 55ECh. 12.5 - Prob. 56ECh. 12.5 - Prob. 57ECh. 12.5 - Prob. 58ECh. 12.5 - Prob. 59ECh. 12.5 - Prob. 60ECh. 12.5 - Prob. 61ECh. 12.5 - Prob. 62ECh. 12.5 - Prob. 63ECh. 12.5 - Motion of a Particle A particle moves along the...Ch. 12.5 - Prob. 65ECh. 12.5 - Prob. 66ECh. 12.5 - Prob. 67ECh. 12.5 - Speed The smaller the curvature of a bend in a...Ch. 12.5 - Prob. 69ECh. 12.5 - Prob. 70ECh. 12.5 - Prob. 71ECh. 12.5 - Prob. 72ECh. 12.5 - Curvature Given the polar curve r=ea,a0, use the...Ch. 12.5 - Prob. 74ECh. 12.5 - Prob. 75ECh. 12.5 - Prob. 76ECh. 12.5 - Prob. 77ECh. 12.5 - Prob. 78ECh. 12.5 - Prob. 79ECh. 12.5 - Prob. 80ECh. 12.5 - Prob. 81ECh. 12.5 - Prob. 82ECh. 12.5 - Prob. 83ECh. 12.5 - Prob. 84ECh. 12.5 - True or False? In Exercises 83-86, determine...Ch. 12.5 - Prob. 86ECh. 12.5 - Prob. 87ECh. 12.5 - Prob. 88ECh. 12.5 - Prob. 89ECh. 12.5 - Prob. 90ECh. 12.5 - Prob. 91ECh. 12.5 - Prob. 92ECh. 12.5 - Kepler's Laws In Exercises 87-94, you are asked to...Ch. 12.5 - Prob. 94ECh. 12.5 - Prob. 95ECh. 12.5 - Prove Keplers Third Law: The square of the period...Ch. 12 - Domain and Continuity In Exercises 1-4, (a) find...Ch. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Writing a Vector-Valued Function In Exercises 7...Ch. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - Evaluating a Definite Integral In Exercises 31-34,...Ch. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Prob. 36RECh. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - 57095-12-40RE-Question-Digital.docx Projectile...Ch. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 44RECh. 12 - Prob. 45RECh. 12 - Prob. 46RECh. 12 - Prob. 47RECh. 12 - Prob. 48RECh. 12 - Prob. 49RECh. 12 - Prob. 50RECh. 12 - Prob. 51RECh. 12 - Prob. 52RECh. 12 - Prob. 53RECh. 12 - Prob. 54RECh. 12 - Prob. 55RECh. 12 - Prob. 56RECh. 12 - Prob. 57RECh. 12 - Prob. 58RECh. 12 - Prob. 59RECh. 12 - Prob. 60RECh. 12 - Prob. 61RECh. 12 - Prob. 62RECh. 12 - Prob. 63RECh. 12 - Prob. 64RECh. 12 - Prob. 65RECh. 12 - Prob. 66RECh. 12 - Prob. 67RECh. 12 - Prob. 68RECh. 12 - Prob. 69RECh. 12 - Prob. 70RECh. 12 - Prob. 71RECh. 12 - Prob. 1PSCh. 12 - Prob. 2PSCh. 12 - Prob. 3PSCh. 12 - Prob. 4PSCh. 12 - Cycloid Consider one arch of the cycloid...Ch. 12 - Prob. 6PSCh. 12 - Prob. 7PSCh. 12 - Prob. 8PSCh. 12 - Prob. 9PSCh. 12 - Prob. 10PSCh. 12 - Prob. 11PSCh. 12 - Prob. 12PSCh. 12 - Prob. 13PSCh. 12 - Ferris Wheel You want to toss an object to a...
Knowledge Booster
Similar questions
- Velocity of a Boat The boater in Exercise 63 wants to arrive at a point on the north shore of the river directly opposite the starting point In what direction should the boat be headed?arrow_forwardInclined Ramp In Exercises 8992, a force of F pounds is required to pull an object weighing W pounds up a ramp inclined at degrees from the horizontal. Find W when F=600 pounds and =14.arrow_forwardDistance a Bullet Travels A bullet is tired into the air at an angle of 45. How far does it travel before it is 1,000 feet above the ground? (Assume that the bullet travels in a straight line; neglect the forces of gravity, and give your answer to the nearest foot.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning  Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning