
Concept explainers
(a) Newton's method for approximating a root of an equation f(x) = 0 (see Section 4.8) can be adapted lo approximating a solution of a system of equations f(x, y) = 0 and g(x, y) = 0. The surfaces z = f(x, y) and z = g(x, y) intersect in a curve that intersects the xy-plane at the point (r, s), which is the solution of the system. If an initial approximation (x1, y1) is close to this point, then the tangent planes to the surfaces at (x1, y1) intersect in a straight line that intersects the xy-plane in a point (x2, y2), which should be closer to (r, s). (Compare with Figure 4.8.2.) Show that
where f, g, and their partial derivatives are evaluated at (x1, y1). If we continue this procedure, we obtain successive approximations (xn, yn).
(b) It was Thomas Simpson (1710–1761) who formulated Newton's method as we know it today and who extended it to functions of two variables as in part (a). (See the biography of Simpson on page 520.) The example that he gave to illustrate the method was to solve the system of equations
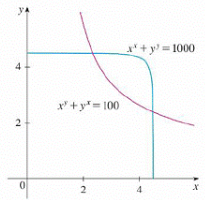
xx + yy= 1000 xy + yx= 100
In other words, he found the points of intersection of the curves in the figure. Use the method of part (a) to find the coordinates of the points of intersection correct to six decimal places.
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
Calculus: Early Transcendentals
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





