
Calculus (MindTap Course List)
11th Edition
ISBN: 9781337275347
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Chapter 14.4, Problem 45E
To determine
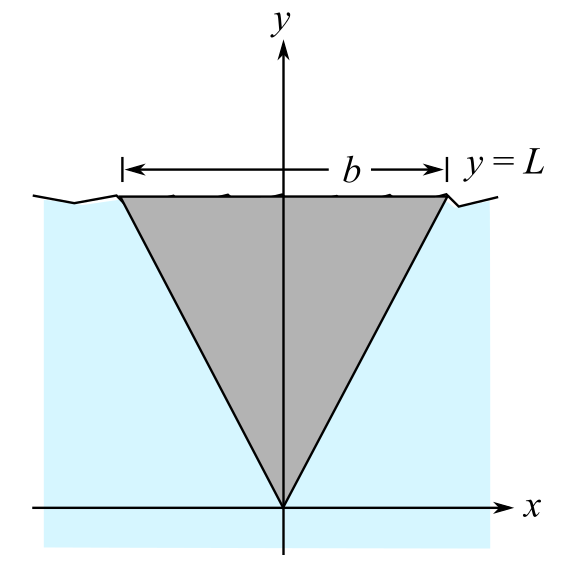
To calculate: The point on the horizontal axis, that is,
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
How do I find the centroid of x + y = 1, coordinate axes?
Mx = integral(b,a)1/2(y2) dx
My = integral(b,a) (xy) dx
A = integral(b,a) y dx
x = My / A
y = Mx / A
PART 1: DETERMINE THE CENTROID IN X (? ") and THE MOMENT INERTIA IN (Iy) OF THE FOLLOWING FIGURE
Consider the motion of a soccer ball that is kicked from the point
x0,y0=⟨0,0⟩ with an initial velocity of u0,v0=⟨35,9⟩ m/s. Assume the x-axis is horizontal, the positive y-axis is vertical (opposite g), the ground is horizontal, and only the gravitational force acts on the object.
Determine the maximum height of the soccer ball.
Chapter 14 Solutions
Calculus (MindTap Course List)
Ch. 14.1 - CONCEPT CHECK Iterated Integral Explain what is...Ch. 14.1 - Prob. 2ECh. 14.1 - Question: Evaluate the integral: 0x(2xy)dyCh. 14.1 - Evaluating an IntegralIn Exercises 310, evaluate...Ch. 14.1 - Evaluating an IntegralIn Exercises 310, evaluate...Ch. 14.1 - Evaluating an IntegralIn Exercises 310, evaluate...Ch. 14.1 - Evaluating an Integral In Exercises 3-10, evaluate...Ch. 14.1 - Evaluating an IntegralIn Exercises 310, evaluate...Ch. 14.1 - Evaluating an Integral In Exercises 3-10, evaluate...Ch. 14.1 - Evaluating an Integral In Exercises 3-10, evaluate...
Ch. 14.1 - Prob. 11ECh. 14.1 - Prob. 12ECh. 14.1 - Prob. 13ECh. 14.1 - Prob. 14ECh. 14.1 - Prob. 15ECh. 14.1 - Prob. 16ECh. 14.1 - Prob. 17ECh. 14.1 - Prob. 18ECh. 14.1 - Evaluating an Iterated Integral In Exercises...Ch. 14.1 - Evaluating an Iterated Integral In Exercises...Ch. 14.1 - Prob. 21ECh. 14.1 - Prob. 22ECh. 14.1 - Evaluating an Iterated Integral In Exercises...Ch. 14.1 - Prob. 24ECh. 14.1 - Prob. 25ECh. 14.1 - Prob. 26ECh. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Evaluating an Improper Iterated Integral In...Ch. 14.1 - Prob. 31ECh. 14.1 - Evaluating an Improper Iterated Integral In...Ch. 14.1 - Finding the Area of a Region In Exercises 33-36,...Ch. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Finding the Area of a Region In Exercises 33-36,...Ch. 14.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - Prob. 40ECh. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 44ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 48ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 50ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 52ECh. 14.1 - Prob. 53ECh. 14.1 - Prob. 54ECh. 14.1 - Prob. 55ECh. 14.1 - Prob. 56ECh. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 60ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 65ECh. 14.1 - Changing the Order of Integration In Exercises...Ch. 14.1 - Prob. 67ECh. 14.1 - Prob. 68ECh. 14.1 - Prob. 69ECh. 14.1 - HOW DO YOU SEE IT? Use each order of integration...Ch. 14.1 - Prob. 71ECh. 14.1 - Prob. 72ECh. 14.1 - Prob. 73ECh. 14.1 - Prob. 74ECh. 14.1 - Prob. 75ECh. 14.1 - Evaluating an Iterated Integral Using Technology...Ch. 14.1 - Prob. 77ECh. 14.1 - Comparing Different Orders of Integration Using...Ch. 14.1 - Prob. 79ECh. 14.1 - Prob. 80ECh. 14.2 - CONCEPT CHECK Approximating the Volume of a Solid...Ch. 14.2 - Prob. 2ECh. 14.2 - Approximation In Exercises 3-6, approximate the...Ch. 14.2 - Approximation In Exercises 3-6, approximate the...Ch. 14.2 - Prob. 5ECh. 14.2 - Prob. 6ECh. 14.2 - Prob. 7ECh. 14.2 - Prob. 8ECh. 14.2 - Prob. 9ECh. 14.2 - Evaluating a Double IntegralIn Exercises 712,...Ch. 14.2 - Prob. 11ECh. 14.2 - Evaluating a Double Integral In Exercises 712,...Ch. 14.2 - Evaluating a Double Integral In Exercises 1320,...Ch. 14.2 - Evaluating a Double IntegralIn Exercises 1320, set...Ch. 14.2 - Evaluating a Double IntegralIn Exercises 1320, set...Ch. 14.2 - Evaluating a Double IntegralIn Exercises 1320, set...Ch. 14.2 - Prob. 17ECh. 14.2 - Prob. 18ECh. 14.2 - Evaluating a Double IntegralIn Exercises 1320, set...Ch. 14.2 - Prob. 20ECh. 14.2 - Prob. 21ECh. 14.2 - Finding Volume In Exercises 21-26, use a double...Ch. 14.2 - Prob. 23ECh. 14.2 - Finding Volume In Exercises 21-26, use a double...Ch. 14.2 - Prob. 25ECh. 14.2 - Finding Volume In Exercises 21-26, use a double...Ch. 14.2 - Prob. 27ECh. 14.2 - Prob. 28ECh. 14.2 - Finding Volume In Exercises 29-34, set up and...Ch. 14.2 - Prob. 30ECh. 14.2 - Prob. 31ECh. 14.2 - Finding Volume In Exercises 29-34, set up and...Ch. 14.2 - Prob. 33ECh. 14.2 - Finding Volume In Exercises 29-34, set up and...Ch. 14.2 - Prob. 35ECh. 14.2 - Prob. 36ECh. 14.2 - Prob. 37ECh. 14.2 - Prob. 38ECh. 14.2 - Prob. 39ECh. 14.2 - Volume of a Region Bounded by Two Surfaces In...Ch. 14.2 - Prob. 41ECh. 14.2 - Prob. 42ECh. 14.2 - Prob. 43ECh. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.2 - Prob. 47ECh. 14.2 - Prob. 48ECh. 14.2 - Prob. 49ECh. 14.2 - Prob. 50ECh. 14.2 - Prob. 51ECh. 14.2 - Prob. 52ECh. 14.2 - Prob. 53ECh. 14.2 - Prob. 54ECh. 14.2 - Average Value In Exercises 51-56. find the average...Ch. 14.2 - Prob. 56ECh. 14.2 - Prob. 57ECh. 14.2 - Prob. 58ECh. 14.2 - Prob. 59ECh. 14.2 - Prob. 60ECh. 14.2 - Prob. 61ECh. 14.2 - Prob. 62ECh. 14.2 - Prob. 63ECh. 14.2 - Prob. 64ECh. 14.2 - Prob. 65ECh. 14.2 - Prob. 66ECh. 14.2 - Prob. 67ECh. 14.2 - Prob. 68ECh. 14.2 - Prob. 69ECh. 14.2 - Prob. 70ECh. 14.2 - Maximizing a Double Integral Determine the region...Ch. 14.2 - Minimizing a Double Integral Determine the region...Ch. 14.2 - Prob. 73ECh. 14.2 - Prob. 74ECh. 14.2 - Prob. 75ECh. 14.2 - Prob. 76ECh. 14.3 - CONCEPT CHECK Choosing a Coordinate System In...Ch. 14.3 - CONCEPT CHECK Choosing a Coordinate SystemIn...Ch. 14.3 - Prob. 3ECh. 14.3 - Prob. 4ECh. 14.3 - Describing a Region In Exercises 58, use polar...Ch. 14.3 - Describing a Region In Exercises 58, use polar...Ch. 14.3 - Prob. 7ECh. 14.3 - Describing a Region In Exercises 58, use polar...Ch. 14.3 - Prob. 9ECh. 14.3 - Evaluating a Double Integral in Exercises 9-16,...Ch. 14.3 - Prob. 11ECh. 14.3 - Evaluating a Double Integral in Exercises 9-16,...Ch. 14.3 - Prob. 13ECh. 14.3 - Prob. 14ECh. 14.3 - Prob. 15ECh. 14.3 - Prob. 16ECh. 14.3 - Converting to Polar Coordinates: In Exercises...Ch. 14.3 - Prob. 18ECh. 14.3 - Converting to Polar Coordinates: In Exercises...Ch. 14.3 - Prob. 20ECh. 14.3 - Converting to Polar Coordinates In Exercises...Ch. 14.3 - Converting to Polar Coordinates: In Exercises...Ch. 14.3 - Prob. 23ECh. 14.3 - Converting to Polar Coordinates: In Exercises...Ch. 14.3 - Prob. 25ECh. 14.3 - Converting to Polar Coordinates: In Exercises...Ch. 14.3 - Prob. 27ECh. 14.3 - Converting to Polar Coordinates: In Exercises 27...Ch. 14.3 - Prob. 29ECh. 14.3 - Prob. 30ECh. 14.3 - Converting to Polar Coordinates In Exercises 2932,...Ch. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - Prob. 35ECh. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Prob. 38ECh. 14.3 - Prob. 39ECh. 14.3 - Prob. 40ECh. 14.3 - Prob. 41ECh. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - Prob. 44ECh. 14.3 - AreaIn Exercises 4146, use a double integral to...Ch. 14.3 - AreaIn Exercises 4146, use a double integral to...Ch. 14.3 - Prob. 47ECh. 14.3 - Prob. 48ECh. 14.3 - Area: In Exercises 4752, sketch a graph of the...Ch. 14.3 - Area: In Exercises 4752, sketch a graph of the...Ch. 14.3 - Prob. 51ECh. 14.3 - Area: In Exercises, 4752, sketch a graph of the...Ch. 14.3 - Prob. 53ECh. 14.3 - Prob. 54ECh. 14.3 - Prob. 55ECh. 14.3 - Prob. 56ECh. 14.3 - Volume Determine the diameter of a hole that is...Ch. 14.3 - Prob. 58ECh. 14.3 - Prob. 59ECh. 14.3 - Prob. 60ECh. 14.3 - Prob. 61ECh. 14.3 - True or False? In Exercises 61 and 62, determine...Ch. 14.3 - Prob. 63ECh. 14.3 - Prob. 64ECh. 14.3 - Prob. 65ECh. 14.3 - Prob. 66ECh. 14.3 - Prob. 67ECh. 14.3 - Area Show that the area of the polar sector R (see...Ch. 14.4 - Mass of a Planar Lamina Explain when you should...Ch. 14.4 - Moment of InertiaDescribe what the moment of...Ch. 14.4 - Finding the Mass of a Lamina In Exercises 3-6,...Ch. 14.4 - Finding the Mass of a Lamina In Exercises 3-6,...Ch. 14.4 - Finding the Mass of a Lamina In Exercises 3-6,...Ch. 14.4 - Prob. 6ECh. 14.4 - Prob. 7ECh. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Prob. 12ECh. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Prob. 15ECh. 14.4 - Prob. 16ECh. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Finding the Center of Mass Using Technology In...Ch. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Finding the Radius of Gyration About Each Axis in...Ch. 14.4 - Prob. 34ECh. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Finding Moments of Inertia and Radii of Gyration...Ch. 14.4 - Prob. 39ECh. 14.4 - Prob. 40ECh. 14.4 - Prob. 41ECh. 14.4 - Prob. 42ECh. 14.4 - Prob. 43ECh. 14.4 - Prob. 44ECh. 14.4 - Prob. 45ECh. 14.4 - Prob. 46ECh. 14.4 - Prob. 47ECh. 14.4 - HOW DO YOU SEE IT? The center of mass of the...Ch. 14.4 - Prob. 49ECh. 14.5 - CONCEPT CHECK Surface Area What is the...Ch. 14.5 - CONCEPT CHECK Numerical Integration Write a double...Ch. 14.5 - Finding Surface AreaIn Exercises 316, find the...Ch. 14.5 - Finding Surface AreaIn Exercises 316, find the...Ch. 14.5 - Finding Surface Area In Exercises 3-16, find the...Ch. 14.5 - Prob. 6ECh. 14.5 - Finding Surface AreaIn Exercises 316, find the...Ch. 14.5 - Prob. 8ECh. 14.5 - Prob. 9ECh. 14.5 - Prob. 10ECh. 14.5 - Prob. 11ECh. 14.5 - Prob. 12ECh. 14.5 - Prob. 13ECh. 14.5 - Prob. 14ECh. 14.5 - Prob. 15ECh. 14.5 - Prob. 16ECh. 14.5 - Finding Surface Area In Exercises 17-20, find the...Ch. 14.5 - Finding Surface Area In Exercises 17-20, find the...Ch. 14.5 - Finding Surface Area In Exercises 17-20, find the...Ch. 14.5 - Prob. 20ECh. 14.5 - Prob. 21ECh. 14.5 - Prob. 22ECh. 14.5 - Prob. 23ECh. 14.5 - Prob. 24ECh. 14.5 - Prob. 25ECh. 14.5 - Prob. 26ECh. 14.5 - Prob. 27ECh. 14.5 - Prob. 28ECh. 14.5 - Prob. 29ECh. 14.5 - Prob. 30ECh. 14.5 - Prob. 31ECh. 14.5 - HOW DO YOU SEE IT? Consider the surface...Ch. 14.5 - Prob. 33ECh. 14.5 - Prob. 34ECh. 14.5 - Product DesignA company produces a spherical...Ch. 14.5 - Modeling Data A company builds a ware house with...Ch. 14.5 - Prob. 37ECh. 14.5 - Prob. 38ECh. 14.6 - CONCEPT CHECK Triple Integrals What does Q=QdV...Ch. 14.6 - Prob. 2ECh. 14.6 - Evaluating a Triple Iterated Integral In Exercises...Ch. 14.6 - Evaluating a Triple Iterated Integral In Exercises...Ch. 14.6 - Prob. 5ECh. 14.6 - Prob. 6ECh. 14.6 - Prob. 7ECh. 14.6 - Prob. 8ECh. 14.6 - Prob. 9ECh. 14.6 - Prob. 10ECh. 14.6 - Evaluating a Triple Iterated Integral Using...Ch. 14.6 - Evaluating a Triple Iterated Integral Using...Ch. 14.6 - Setting Up a Triple IntegralIn Exercises 13-18,...Ch. 14.6 - Setting Up a Triple IntegralIn Exercises 13-18,...Ch. 14.6 - Setting Up a Triple IntegralIn Exercises 13-18,...Ch. 14.6 - Setting Up a Triple IntegralIn Exercises 13-18,...Ch. 14.6 - Prob. 17ECh. 14.6 - Prob. 18ECh. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Volume In Exercises 19-24, use a triple integral...Ch. 14.6 - Changing the Order of integration In Exercises...Ch. 14.6 - Changing the Order of integration In Exercises...Ch. 14.6 - Prob. 27ECh. 14.6 - Prob. 28ECh. 14.6 - Changing the Order of Integration In Exercises...Ch. 14.6 - Changing the Order of integration In Exercises...Ch. 14.6 - Orders of Integration In Exercises 31-34, write a...Ch. 14.6 - Orders of Integration In Exercises 31-34, write a...Ch. 14.6 - Prob. 33ECh. 14.6 - Prob. 34ECh. 14.6 - Prob. 35ECh. 14.6 - Orders of Integration In Exercises 35 and 36, the...Ch. 14.6 - Prob. 37ECh. 14.6 - Prob. 38ECh. 14.6 - Prob. 39ECh. 14.6 - Center of Mass In Exercises 37-40, find the mass...Ch. 14.6 - Center of Mass In Exercises 41 and 42, set up the...Ch. 14.6 - Prob. 42ECh. 14.6 - Think About It The center of mass of a solid of...Ch. 14.6 - Prob. 44ECh. 14.6 - Think About It The center of mass of a solid of...Ch. 14.6 - Think About It The center of mass of a solid of...Ch. 14.6 - Centroid In Exercises 47-52, find the centroid of...Ch. 14.6 - Centroid In Exercises 47-52, find the centroid of...Ch. 14.6 - Prob. 49ECh. 14.6 - Centroid In Exercises 47-52, find the centroid of...Ch. 14.6 - Prob. 51ECh. 14.6 - Prob. 52ECh. 14.6 - Moments of Inertia In Exercises 53- 56, find...Ch. 14.6 - Moments of Inertia In Exercises 53- 56, find...Ch. 14.6 - Moments of Inertia In Exercises 53- 56, find...Ch. 14.6 - Prob. 56ECh. 14.6 - Prob. 57ECh. 14.6 - Prob. 58ECh. 14.6 - Moments of Inertia In Exercises 59 and 60, set up...Ch. 14.6 - Moments of Inertia In Exercises 59 and 60, set up...Ch. 14.6 - Prob. 61ECh. 14.6 - Prob. 62ECh. 14.6 - Prob. 63ECh. 14.6 - Prob. 64ECh. 14.6 - Prob. 65ECh. 14.6 - Prob. 66ECh. 14.6 - Prob. 67ECh. 14.6 - Prob. 68ECh. 14.6 - Prob. 69ECh. 14.6 - Prob. 70ECh. 14.6 - Prob. 71ECh. 14.6 - Prob. 72ECh. 14.6 - Prob. 73ECh. 14.7 - CONCEPT CHECK Volume Explain why triple integrals...Ch. 14.7 - CONCEPT CHECK Differential of Volume What is the...Ch. 14.7 - Prob. 3ECh. 14.7 - Prob. 4ECh. 14.7 - Prob. 5ECh. 14.7 - Prob. 6ECh. 14.7 - Prob. 7ECh. 14.7 - Prob. 8ECh. 14.7 - Prob. 9ECh. 14.7 - Prob. 10ECh. 14.7 - Prob. 11ECh. 14.7 - VolumeIn Exercises 1114, sketch the solid region...Ch. 14.7 - Volume In Exercises 11-14, sketch the solid region...Ch. 14.7 - Volume In Exercises 11-14, sketch the solid region...Ch. 14.7 - Prob. 15ECh. 14.7 - Volume In Exercises 15-20, use cylindrical...Ch. 14.7 - VolumeIn Exercises 1520, use cylindrical...Ch. 14.7 - Volume In Exercises 15-20, use cylindrical...Ch. 14.7 - VolumeIn Exercises 1520, use cylindrical...Ch. 14.7 - Volume In Exercises 15-20, use cylindrical...Ch. 14.7 - Prob. 21ECh. 14.7 - Prob. 22ECh. 14.7 - Prob. 23ECh. 14.7 - Prob. 24ECh. 14.7 - Prob. 27ECh. 14.7 - Prob. 29ECh. 14.7 - VolumeIn Exercises 3134, use spherical coordinates...Ch. 14.7 - VolumeIn Exercises 3134, use spherical coordinates...Ch. 14.7 - Prob. 33ECh. 14.7 - Prob. 34ECh. 14.7 - Prob. 35ECh. 14.7 - MassIn Exercises 35 and 36, use spherical...Ch. 14.7 - Prob. 37ECh. 14.7 - Center of MassIn Exercises 37 and 38, use...Ch. 14.7 - Prob. 39ECh. 14.7 - Prob. 40ECh. 14.7 - Converting CoordinatesIn Exercises 4144, convert...Ch. 14.7 - Converting CoordinatesIn Exercises 4144, convert...Ch. 14.7 - Converting CoordinatesIn Exercises 4144, convert...Ch. 14.7 - Prob. 45ECh. 14.7 - HOW DO YOU SEE IT? The solid is bounded below by...Ch. 14.7 - Prob. 47ECh. 14.8 - CONCEPT CHECK JacobianDescribe how to find the...Ch. 14.8 - CONCEPT CHECK Change of VariableWhen is it...Ch. 14.8 - Prob. 3ECh. 14.8 - Prob. 4ECh. 14.8 - Prob. 5ECh. 14.8 - Prob. 6ECh. 14.8 - Prob. 7ECh. 14.8 - Prob. 8ECh. 14.8 - Prob. 9ECh. 14.8 - Prob. 10ECh. 14.8 - Prob. 11ECh. 14.8 - Using a Transformation In Exercises 11-14, sketch...Ch. 14.8 - Prob. 13ECh. 14.8 - Using a Transformation In Exercises 11-14, sketch...Ch. 14.8 - Prob. 15ECh. 14.8 - Prob. 16ECh. 14.8 - Prob. 17ECh. 14.8 - Evaluating a Double Integral Using a Change of...Ch. 14.8 - Evaluating a Double Integral Using a Change of...Ch. 14.8 - Evaluating a Double Integral Using a Change of...Ch. 14.8 - Evaluating a Double Integral Using a Change of...Ch. 14.8 - Evaluating a Double Integral Using a Change of...Ch. 14.8 - Prob. 23ECh. 14.8 - Prob. 24ECh. 14.8 - Finding Volume Using a Change of Variables In...Ch. 14.8 - Finding Volume Using a Change of Variables In...Ch. 14.8 - Prob. 27ECh. 14.8 - Finding Volume Using a Change of Variables In...Ch. 14.8 - Prob. 29ECh. 14.8 - Prob. 30ECh. 14.8 - Prob. 31ECh. 14.8 - Prob. 32ECh. 14.8 - Prob. 33ECh. 14.8 - VolumeUse the result of Exercise 33 to find the...Ch. 14.8 - Prob. 35ECh. 14.8 - Prob. 36ECh. 14.8 - Prob. 37ECh. 14.8 - Prob. 38ECh. 14.8 - Prob. 39ECh. 14.8 - Prob. 40ECh. 14.8 - Prob. 41ECh. 14 - Prob. 1RECh. 14 - Prob. 2RECh. 14 - Prob. 3RECh. 14 - Prob. 4RECh. 14 - Prob. 5RECh. 14 - Prob. 6RECh. 14 - Prob. 7RECh. 14 - Prob. 8RECh. 14 - Prob. 9RECh. 14 - Prob. 10RECh. 14 - Prob. 11RECh. 14 - Prob. 12RECh. 14 - Prob. 13RECh. 14 - Prob. 14RECh. 14 - Prob. 15RECh. 14 - Prob. 16RECh. 14 - Finding Volume In Exercises 17-20, use a double...Ch. 14 - Prob. 18RECh. 14 - Prob. 19RECh. 14 - Prob. 20RECh. 14 - Prob. 21RECh. 14 - Prob. 22RECh. 14 - Prob. 23RECh. 14 - Prob. 24RECh. 14 - Converting to Polar CoordinatesIn Exercises 25 and...Ch. 14 - Prob. 26RECh. 14 - VolumeIn Exercises 27 and 28, use a double...Ch. 14 - Prob. 28RECh. 14 - Prob. 29RECh. 14 - Prob. 30RECh. 14 - Prob. 31RECh. 14 - Prob. 32RECh. 14 - Area and VolumeConsider the region R in the xy...Ch. 14 - Converting to Polar Coordinates Write the sum of...Ch. 14 - Prob. 35RECh. 14 - Prob. 36RECh. 14 - Finding the Center of MassIn Exercises 3740, find...Ch. 14 - Prob. 38RECh. 14 - Prob. 39RECh. 14 - Prob. 40RECh. 14 - Prob. 41RECh. 14 - Prob. 42RECh. 14 - Prob. 43RECh. 14 - Finding Surface AreaIn Exercises 4346, find the...Ch. 14 - Prob. 45RECh. 14 - Prob. 46RECh. 14 - Building DesignA new auditorium is built with a...Ch. 14 - Prob. 48RECh. 14 - Prob. 49RECh. 14 - Prob. 50RECh. 14 - Prob. 51RECh. 14 - Prob. 52RECh. 14 - Prob. 53RECh. 14 - Prob. 54RECh. 14 - VolumeIn Exercises 55 and 56, use a triple...Ch. 14 - Prob. 56RECh. 14 - Prob. 57RECh. 14 - Prob. 59RECh. 14 - Prob. 60RECh. 14 - Prob. 61RECh. 14 - Prob. 62RECh. 14 - Prob. 63RECh. 14 - Prob. 64RECh. 14 - Prob. 65RECh. 14 - Prob. 66RECh. 14 - VolumeIn Exercises 67 and 68, use cylindrical...Ch. 14 - Prob. 68RECh. 14 - Prob. 69RECh. 14 - Prob. 70RECh. 14 - Prob. 71RECh. 14 - Prob. 72RECh. 14 - Finding a JcobianIn Exercises 7174, find the...Ch. 14 - Prob. 74RECh. 14 - Prob. 75RECh. 14 - Evaluating a Double Integral Using a Change of...Ch. 14 - Prob. 77RECh. 14 - Prob. 78RECh. 14 - Prob. 1PSCh. 14 - Prob. 2PSCh. 14 - Prob. 3PSCh. 14 - Prob. 4PSCh. 14 - Prob. 5PSCh. 14 - Prob. 6PSCh. 14 - Prob. 7PSCh. 14 - Prob. 8PSCh. 14 - Prob. 9PSCh. 14 - Prob. 10PSCh. 14 - Prob. 11PSCh. 14 - Prob. 12PSCh. 14 - Prob. 14PSCh. 14 - Prob. 15PSCh. 14 - Prob. 16PSCh. 14 - Prob. 18PS
Knowledge Booster
Similar questions
- The figure shows the side view of a portable traffic signal. The upper portion of the signal with attached frame has a mass of 90 kg with mass center at G. The signal and frame are hinged at point E and rest on a vertical post at H. In operation, member DEH is positioned vertically by means of the hand-operated winch so that the lights are directed to the left. Determine the necessary input force F that will just start to rotate the signal from its horizontal position. Note that handle A is rigidly attached to gear B. The dimension (AB) ̅=200 mm.arrow_forward3. Find the coordinates of the centroid of the triangle enclosed by x = 1, y = 0,and y = 4x.arrow_forwardLocate the centroid of the solid generated when the area of x^2 + y^2 = a^2 in the first quadrant and the fourth quadrant by 2x - y = 2a and x = 0 about x = 0, a. (0, 2a/3) b. (0,-2a/3) c. (0,-a/16) d, (0, a/16)arrow_forward
- Find the circulation of fluid motion F⃑(x, y) = xi⃑ − xyj⃑ along positively oriented ellipse x2 + 4y2 = 4.arrow_forwardShow that the centroid of the solid semiellipsoid of revolution (r2/a2 ) + (z2/h2 )<=1, z>=0, lies on the z-axis three-eighths of the way from the base to the top. The special case h = a gives a solid hemisphere. Thus, the centroid of a solid hemisphere lies on the axis of symmetry three-eighths of the way from the base to the top.arrow_forwardA rock moves along the parabola x=y^2+2 under the forcefield F=(x2, y^ex). Find the work moving the rock from (2,0) to (3,1).arrow_forward
- Find the Jacobian for a cylindrical system.arrow_forwardEvaluate the outward flux of the vector field F(x,y,z) = (x, -y, z) across the surface S: x2 +y2 =4, 0 <= z <= 1. Use a parametric description of the cylinder surface.arrow_forwardUse Stokes' Theorem to find the work done on a particle moves along the line segments from the origin to the points (2,0,0) (2,4,3) , (0,4,3). and back to the origin. Note that this (counterclockwise) path is a rectangle on the plane z = 3/4 y. The motion is under the influence of the force field F = z2 i+ 2xy j + 4y2 karrow_forward
- Let C be a triangle with verticies (0,0), (2,0), and (0,5) oriented in the counterclockwise direction. Calculate the outward flux of F(x,y)=−xi+2yj across C.arrow_forwardPart A: IG=27, Find CI Part B: In △RST,X△RST,X is the centroid. If SX=14,SX=14, find XWXW and SW.arrow_forwardRain on a roof Consider the vertical vector field F = ⟨0, 0, -1⟩, correspondingto a constant downward flow. Find the flux in the downward direction acrossthe surface S, which is the plane z = 4 - 2x - y in the first octant.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage