
Two distances are required to specify the location of a point relative to an origin in two-dimensional space (Fig. P2.14):
The horizontal and vertical distances
The radius and angle
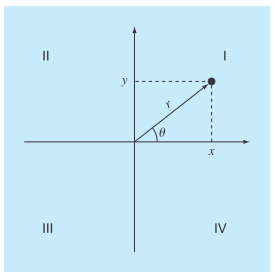
FIGURE P2.14
It is relatively straight forward to compute Cartesian coordinates
If the coordinates lie within the first and fourth coordinates
The difficulty arises for the other cases. The following table summarizes the possibilities:
| x | Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
(a) Write a well-structured flowchart for a subroutine procedure to calculate r and
(b) Write a well-structured function procedure based on your flowchart. Test your program by using it to fill out the following table:
| x | Y | r |
|
| 1 | 0 | ||
| 1 | 1 | ||
| 0 | 1 | ||
| –1 | 1 | ||
| –1 | 0 | ||
| –1 | –1 | ||
| 0 | –1 | ||
| 1 | –1 | ||
| 0 | 0 |
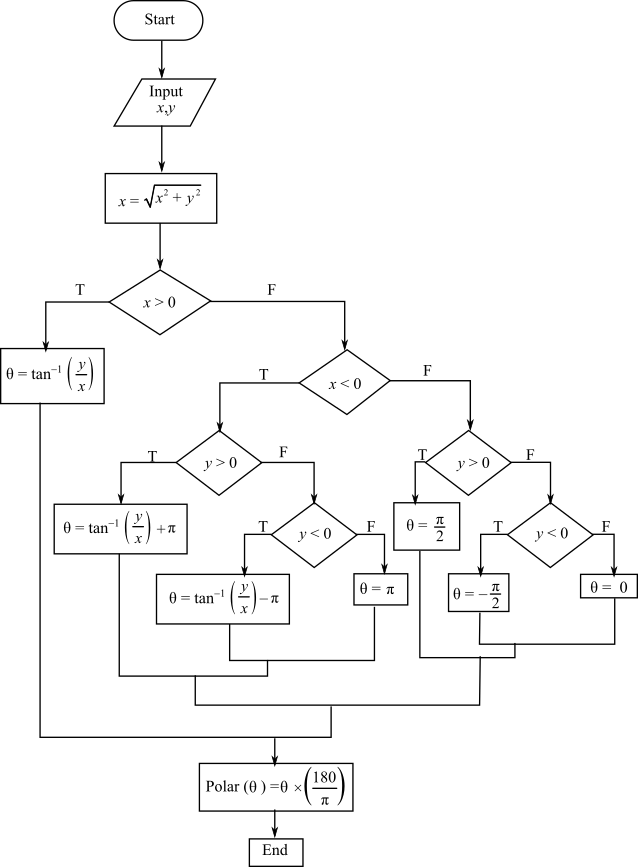
(a)
A well-structured flowchart for a subordinate procedure to calculate r and
Answer to Problem 14P
Solution:
Explanation of Solution
Given Information:
To specify the location of a point relative to origin, cartesian coordinates
Cartesian coordinates can be easily computed from the polar coordinates.
Polar coordinates are computed as follows:
Formula used:
Calculation:
The flowchart for converting from Cartesian to polar coordinates is as follows

(b)
A well-structured function procedure based on flowchart of part (a) if two distances are required to specify the location of a point relative to an origin in two-dimensional space. Also, test the program by filling the table given below:
Answer to Problem 14P
Solution:
The values of r and
Explanation of Solution
Given Information:
To specify the location of a point relative to origin, cartesian coordinates
Cartesian coordinates can be easily computed from the polar coordinates.
Polar coordinates are computed as follows:
Calculation:
The MATLAB program for converting Cartesian to polar coordinates is as follows:
% Define a function polar()
function polar(x, y)
% Formula to calculate r
r = sqrt (x.^ 2+ y.^ 2);
if x > 0
% Formula to calculate theta
th= atan(y/ x);
elseif x < 0
% Use for loop to check the condition
if y > 0
th= atan(y / x)+ pi;
elseif y < 0
th= atan(y / x)- pi;
else
th= pi;
end
else
if y > 0
th= pi / 2;
elseif y < 0
th=- pi / 2;
else
th= 0;
end
end
theta = th* 180 / pi;
% Display the polar coordinates
fprintf('r = %4.4f theta = %4.2f\n',r,theta);
Now, to test the program use the following command.
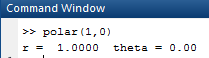
First find polar coordinates for
OUTPUT:
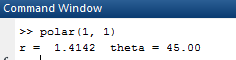
Now, for polar coordinates for
OUTPUT:
Now, for polar coordinates for
OUTPUT:
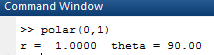
Now, forpolar coordinates for
OUTPUT:
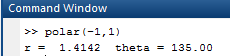
Now, forpolar coordinates for
OUTPUT:
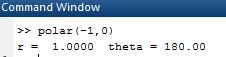
Now, forpolar coordinates for
OUTPUT:

Now, forpolar coordinates for
OUTPUT:
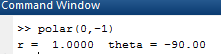
Now, forpolar coordinates for
OUTPUT:
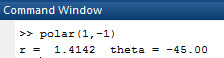
Now, forpolar coordinates for
OUTPUT:
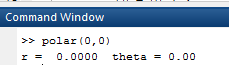
Hence, the values of r and
Want to see more full solutions like this?
Chapter 2 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Fundamentals of Differential Equations (9th Edition)
Advanced Engineering Mathematics
Basic Technical Mathematics
Algebra and Trigonometry (6th Edition)
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
