
(a)
To show that the minimum spanning tree is unique but not the second best spanning tree.
(a)
Explanation of Solution
Suppose there are 4 vertices { p, q, r, s } in the following graph. Consider the edge weights and vertices as follows:
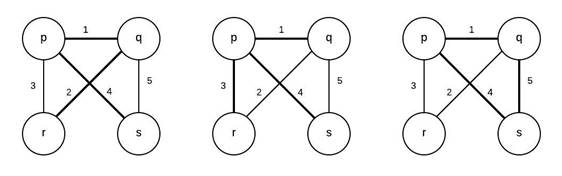
The minimum spanning tree has weight of 7 and there exists two second best minimum spanning tree having weight 8.
(b)
To prove that there exists edges ( u , v )
(b)
Explanation of Solution
T is the minimum spanning tree of graph G . Consider adding an edge that is ( u , v )
(c)
To describe an O (
(c)
Explanation of Solution
The algorithm is as follows:
Consider using dynamic
(d)
To give an efficient algorithm to compute the second-best minimum spanning tree of graph G.
(d)
Explanation of Solution
Firstly, compute the minimum spanning tree in O ( E + Vlog ( V )), this is in time O (
Want to see more full solutions like this?
- Let A, B, C, D be the vertices of a square with side length 100. If we want to create a minimum-weight spanning tree to connect these four vertices, clearly this spanning tree would have total weight 300 (e.g. we can connect AB, BC, and CD). But what if we are able to add extra vertices inside the square, and use these additional vertices in constructing our spanning tree? Would the minimum-weight spanning tree have total weight less than 300? And if so, where should these additional vertices be placed to minimize the total weight? Let G be a graph with the vertices A, B, C, D, and possibly one or more additional vertices that can be placed anywhere you want on the (two-dimensional) plane containing the four vertices of the square. Determine the smallest total weight for the minimum-weight spanning tree of G. Round your answer to the nearest integer. Attention: Please don't just copy these two following answers, which are not correct at all. Thank you.…arrow_forwardG = (V,E,W) is a weighted connected (undirected) graph where all edges have distinct weights except two edges e and e′ which have the same weight. Suppose there is a Minimum Spanning Tree of G containing both e and e′. Prove that G has a unique Minimum Spanning Tree.arrow_forwardLet G = (V, E) be an undirected graph and each edge e ∈ E is associated with a positive weight ℓ(e).For simplicity we assume weights are distinct. Is the following statement true or false? Prove by contradiction or counterexample. Let T be a minimum spanning tree for the graph with the original weight. Suppose we replace eachedge weight ℓ(e) with ℓ(e)^2, then T is still a minimum spanning tree.arrow_forward
- Let G = (V, E) be a connected, undirected graph, and let s be a fixed vertex in G. Let TB be the spanning tree of G found by a bread first search starting from s, and similarly TD the spanning tree found by depth first search, also starting at s. (As in problem 1, these trees are just sets of edges; the order in which they were traversed by the respective algorithms is irrelevant.) Using facts, prove that TB = TD if and only if TB = TD = E, i.e., G is itself a tree.arrow_forward. Let G be a weighted, connected, undirected graph, and let V1 and V2 be a partition of the vertices of G into two disjoint nonempty sets. Furthermore, let e be an edge in the minimum spanning tree for G such that e has one endpoint in V1 and the other in V2. Give an example that shows that e is not necessarily the smallest- weight edge that has one endpoint in V1 and the other in V2.arrow_forwarda) Draw the connected subgraph of the given graph above which contains only four nodes ACGB and is also a minimum spanning tree with these four nodes. What is its weighted sum? Draw the adjacency matrix representation of this subgraph (use boolean matrix with only 0 or 1, to show its adjacency in this case).b) Find the shortest path ONLY from source node D to destination node G of the given graph above, using Dijkstra’s algorithm. Show your steps with a table as in our course material, clearly indicating the node being selected for processing in each step.c) Draw ONLY the shortest path obtained above, and indicate the weight in each edge in the diagram. Also determine the weighted sumarrow_forward
- Let G = (V, E) be an undirected graph and each edge e ∈ E is associated with a positive weight ℓ(e).For simplicity we assume weights are distinct. Is the following statement true or false? Let T be a minimum spanning tree for the graph with the original weight. Suppose we replace eachedge weight ℓ(e) with ℓ(e)^2, then T is still a minimum spanning tree.arrow_forwardAlgorithm: Network Flow(Maximu Flow, Ford-Fulkerson) and Application of Flow (Minimum Cuts, Bipartite Matching) Consider a flow network and an arbitrary s, t-cut (S, T). We know that by definition s must always be on the S "side" of a cut and t is always going to be on the T "side" of the cut. Obviously, this is true for any cut. Now, consider minimum cuts. This is obviously still true for s and t, but what about other vertices in the flow network? Are there vertices that will always be on one side or the other in every minimum cut? Let's define these notions more concretely. • We say a vertex v is source-docked if v ∈ S for all minimum cuts (S, T). • We say a vertex v is sink-docked if v ∈ T for all minimum cuts (S, T). • We say a vertex v is undocked if v is neither source-docked nor sink-docked. That is, there exist minimum cuts (S, T) and (S 0 , T0 ) such that v ∈ S and v ∈ T' Give an algorithm that takes as input a flow network G and assigns each vertex to one of the three…arrow_forwardGiven an undirected weighted graph G with n nodes and m edges, and we have used Prim’s algorithm to construct a minimum spanning tree T. Suppose the weight of one of the tree edge ((u, v) ∈ T) is changed from w to w′, design an algorithm to verify whether T is still a minimum spanning tree. Your algorithm should run in O(m) time, and explain why your algorithm is correct. You can assume all the weights are distinct. (Hint: When an edge is removed, nodes of T will break into two groups. Which edge should we choose in the cut of these two groups?)arrow_forward
- True or false: let G be an arbitrary connected, undirected graph with a distinct cost c(e) on every edge e. suppose e* is the cheapest edge in G; that is, c(e*) <c(e) for every edge e is not equal to e*. Any minimum spanning tree T of G contains the edge e*arrow_forwardSuppose there is undirected graph F with nonnegative edge weights we ≥ 0. You have also calculated the minimum spanning tree of F and also the shortest paths to all nodes from a particular node p ∈ V . Now, suppose that each edge weight is increased by 1, so the new weights are we′ = we + 1. (a) Will there be a change of the minimum spanning tree? Provide an example where it does or prove that it cannot change. (b) (3 points) Will the shortest paths from p change? Provide an example where it does or prove that it cannot change.arrow_forwardLet G = (V, E) denote an weighted undirected graph, in which every edge has unit weight, and let T = (V, E') denote the minimum spanning tree of G. Prove formally that for all u, v ∈ V , the path between u and v in tree T is uniquearrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





