
Locate the first positive root of
Where x is in radians. Use four iterations of the secant method with initial guesses of (a)
(a)
To calculate: Thefirst positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 3 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(b)
To calculate: The first positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 2.5 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(c)
To calculate: The first positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | ||
| 1 | 16.76% | |
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(d)
The explanation of the result obtained by the secant method of the function
Answer to Problem 7P
Solution:
For the initial guesses
For the initial guesses
For the initial guesses
Explanation of Solution
Given Information:
The function,
Consider the function,
From part (a), the result obtained with the initial guesses
| 0 | 3 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
end
Output:
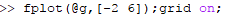
The graph obtained is,
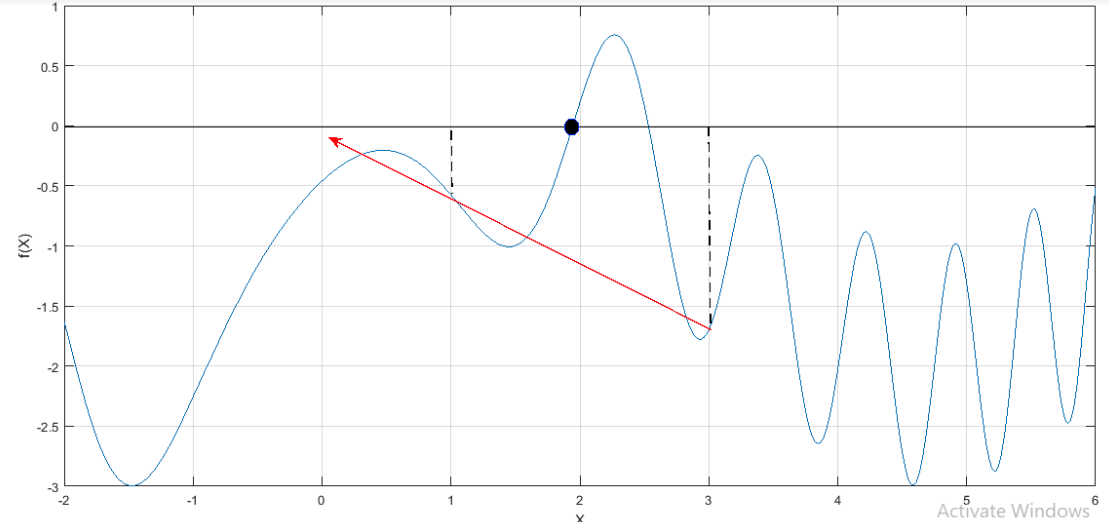
From the graph, it is observed that the first iteration gives a negative value due to the improper choice of initial guess.
From part (b), the result obtained with the initial guesses
| 0 | 2.5 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
end
Output:
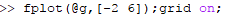
The graph obtained is,
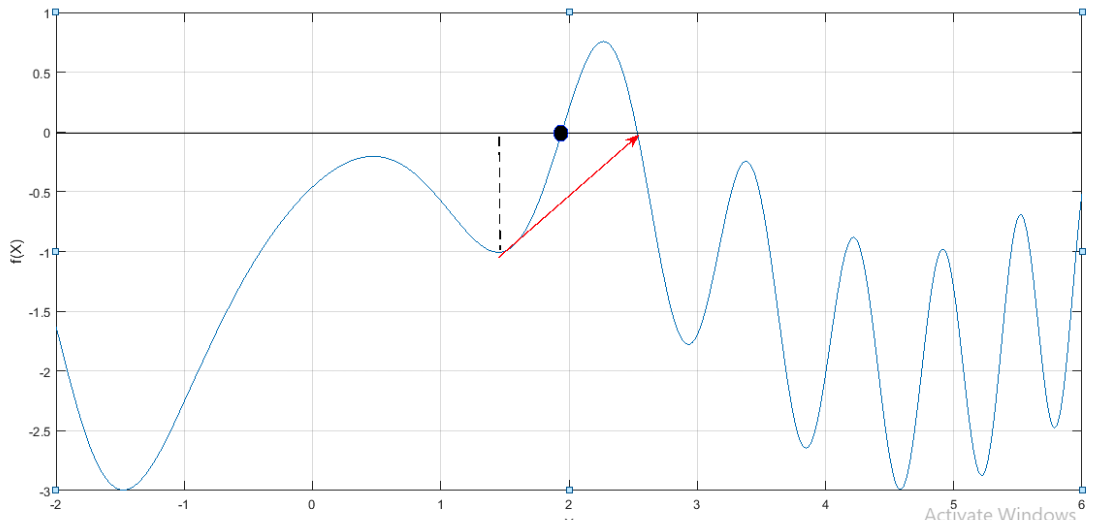
From the graph, it is observed that the root is converges towards the second positive root with these initial guesses instead of first positive root.
From part (c), the result obtained with the initial guesses
| 0 | ||
| 1 | 16.76% | |
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
Output:
The graph obtained is,
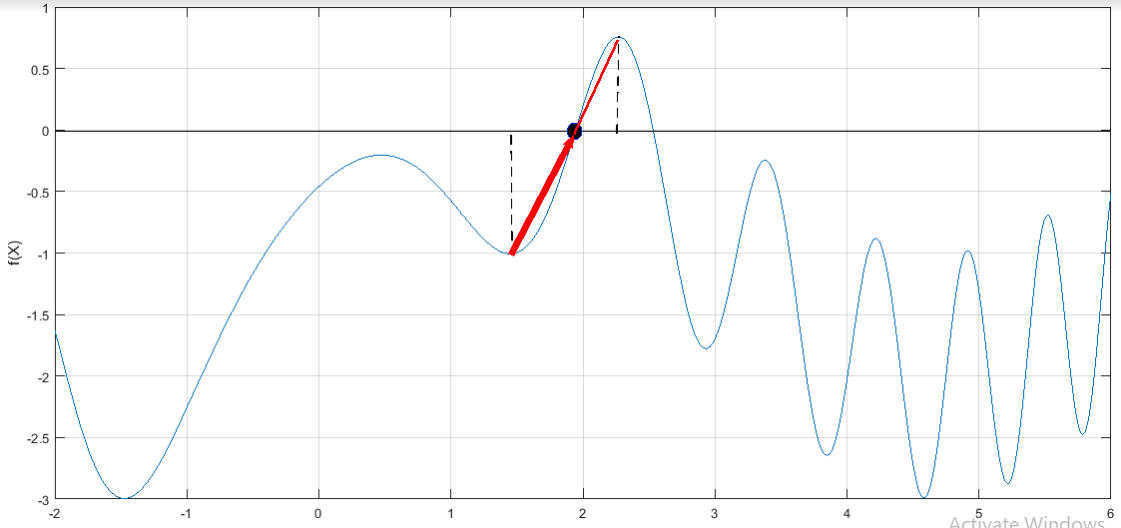
From the graph, it is observed that the root is converges towards the first positive root with these initial guesses rapidly. Hence, these guesses are the proper selection to locate the first positive root by secant method.
Want to see more full solutions like this?
Chapter 6 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Basic Technical Mathematics
Advanced Engineering Mathematics
Fundamentals of Differential Equations (9th Edition)
Elementary Statistics Using Excel (6th Edition)
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
