
1-4 Modeling Periodic Data A set of data is given.
(a) Make a
(b) Find a cosine function of the form
(c) Graph the function you found in part (b) together with the scatter plot. How well does the curve fit the data?
(d) Use a graphing calculator to find the sine function that best fits the data, as in Example 2.
(e) Compare the functions you found in parts (b) and (d). [Use the reduction formula
| t | y |
| 0 | 2.1 |
| 2 | 1.1 |
| 4 |
|
| 6 |
|
| 8 |
|
| 10 | 0.6 |
| 12 | 1.9 |
| 14 | 1.5 |
(a)
To find:
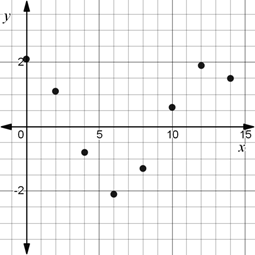
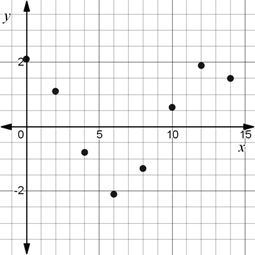
A scatter plot of the data.
Answer to Problem 1P
Solution:
Explanation of Solution
Calculation:
The scatter plot for the given data is given by
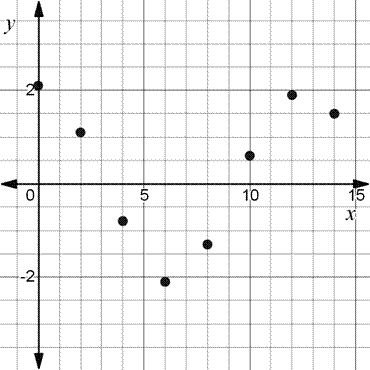
Final statement:
(b)
To find:
A cosine function of the form
Answer to Problem 1P
Solution:
Explanation of Solution
Calculation:
Here, the maximum value is 2.1 and the minimum value is -2.1.
The maximum value occurs at time 0 and the minimum value occurs at time 6.
The vertical shift
The amplitude
The time between consecutive maximum and minimum values is half of one period.
That is,
Since the maximum value of the data occurs at
There is no horizontal shift.
Apply the values in the function
Since cosine is an even function,
Final statement:
(c)
To find:
The graph of the function from part (b).
Answer to Problem 1P
Solution:
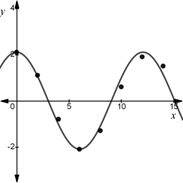
Explanation of Solution
Calculation:
The graph of the function

Final statement:
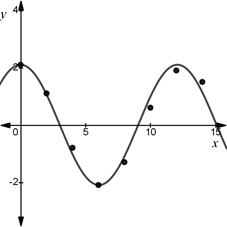
(d)
To find:
The sine function that fits the data.
Answer to Problem 1P
Solution:
Explanation of Solution
Calculation:
Using the given data and the SinReg command on the T1-83 calculator, we get a function of the form
Here,
Apply the values in the function
Final statement:
(e)
To find:
The comparison between the functions from part (b) and (d).
Answer to Problem 1P
Solution:
It is same as (b), corrected to one decimal.
Explanation of Solution
Calculation:
From part (d),
Apply the reduction formula
So,
It is same as (b), corrected to one decimal.
Final statement:
It is same as (b), corrected to one decimal.
Want to see more full solutions like this?
Chapter 6 Solutions
Algebra and Trigonometry (MindTap Course List)
Additional Math Textbook Solutions
College Algebra (5th Edition)
Elementary and Intermediate Algebra
Linear Algebra and Its Applications (5th Edition)
College Algebra
College Algebra
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
- View from a Satellite The figures on the next page indicate that the higher the orbit of satellite, the more of the earth the satellite can see. Let ,s, and h be as in the figure, and assume that the earth is a sphere of radius 3960 mi. a Express the angle as a function of h. b Express the distance s as a function of . c Express the distance s as a function of h. Hint: Find the composition of the functions in parts a and b. d If the satellite is 100 mi above the earth, what is the distance s that it can see? e How high does the satellite have to be to see both Los Angeles and New York, 2450 mi apart?arrow_forwardSimple Harmonic Motion A mass suspended from a spring oscillates in simple harmonic motion at a frequency of 4 cycles per second. The distance from the highest to the lowest point of the oscillation is 100 cm. Find an equation that describes the distance of the mass from its rest position as a function of time. Assume that the mass is at its lowest point when t=0.arrow_forwardOscillating Spring A mass attached to a spring oscillates upward and downward. The displacement of the mass from its equilibrium position after t seconds is given by the function d=3.5cos(2t). where d is measured in centimeters (Figure 13). a. Sketch the graph of this function for 0t5. b. What is the furthest distance of the mass from its equilibrium position? c. How long does it take for the mass to complete one oscillation?arrow_forward
- CONCEPTS For an object in simple harmonic motion with amplitude a and period 2/, find an equation that models the displacement y at any time t if a y=0 at time t=0: y= ____________. b y=a at time t=0: y= ____________.arrow_forwardPhotography A photographer takes a picture of a three-foot-tall painting hanging in an art gallery. The camera lens is 1 foot below the lower edge of the painting (see figure). The angle subtended by the camera lens x feet from the painting is given by =arctan3xx2+4,x0. (a) Use a graphing utility to graph as a function of x. (b) Use the graph to approximate the distance from the picture when is maximum. (c) Identify the asymptote of the graph and interpret its meaning in the context of the problem.arrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning



